Data Structure and Algorithms - B Trees

---

B trees are extended binary search trees that are specialized in m-way searching, since the order of B trees is ‘m’. Order of a tree is defined as the maximum number of children a node can accommodate. Therefore, the height of a b tree is relatively smaller than the height of AVL tree and RB tree.

They are general form of a Binary Search Tree as it holds more than one key and two children.

The various properties of B trees include −

• Every node in a B Tree will hold a maximum of m children and (m-1) keys, since the order of the tree is m.

• Every node in a B tree, except root and leaf, can hold at least m/2 children

• The root node must have no less than two children.

• All the paths in a B tree must end at the same level, i.e. the leaf nodes must be at the same level.

• A B tree always maintains sorted data.

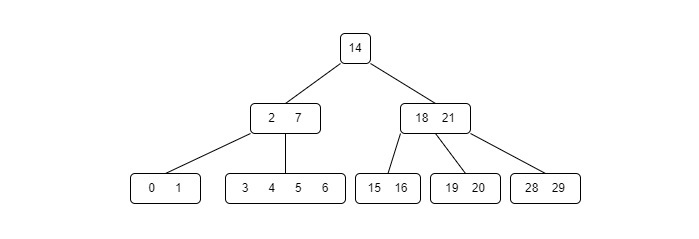
B trees are also widely used in disk access, minimizing the disk access time since the height of a b tree is low.

Note − A disk access is the memory access to the computer disk where the information is stored and disk access time is the time taken by the system to access the disk memory.

Basic Operations of B Trees

The operations supported in B trees are Insertion, deletion and searching with the time complexity of O(log n) for every operation.

Insertion

The insertion operation for a B Tree is done similar to the Binary Search Tree but the elements are inserted into the same node until the maximum keys are reached. The insertion is done using the following procedure −

Step 1 − Calculate the maximum $\mathrm{\left ( m-1 \right )}$ and minimum $\mathrm{\left ( \left \lceil \frac{m}{2}\right \rceil-1 \right )}$ number of keys a node can hold, where m is denoted by the order of the B Tree.

Step 2 − The data is inserted into the tree using the binary search insertion and once the keys reach the maximum number, the node is split into half and the median key becomes the internal node while the left and right keys become its children.

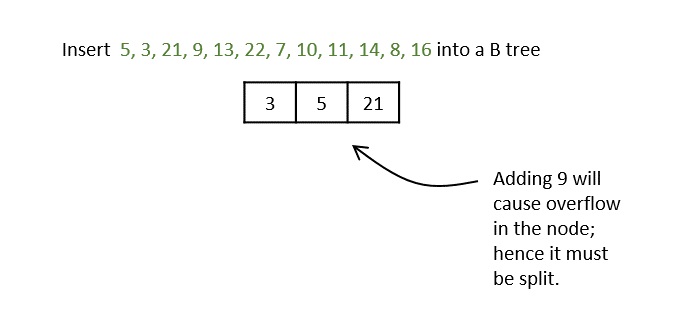
Step 3 − All the leaf nodes must be on the same level.

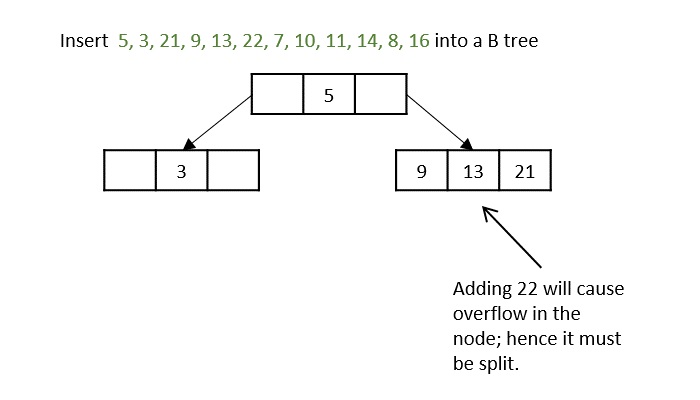
The keys, 5, 3, 21, 9, 13 are all added into the node according to the binary search property but if we add the key 22, it will violate the maximum key property. Hence, the node is split in half, the median key is shifted to the parent node and the insertion is then continued.

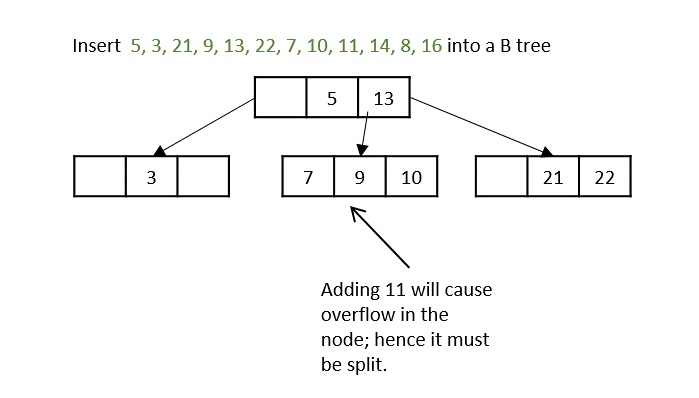
Another hiccup occurs during the insertion of 11, so the node is split and median is shifted to the parent.

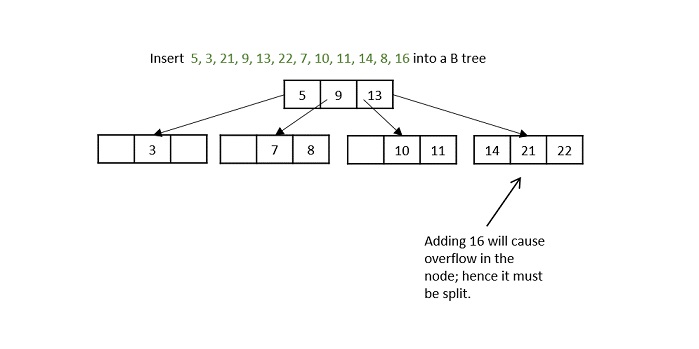
While inserting 16, even if the node is split in two parts, the parent node also overflows as it reached the maximum keys. Hence, the parent node is split first and the median key becomes the root. Then, the leaf node is split in half the median of leaf node is shifted to its parent.

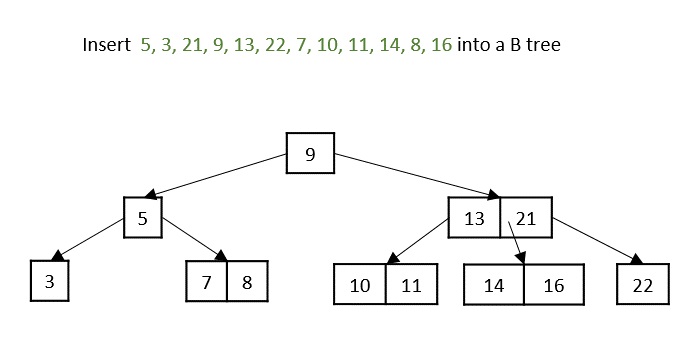
The final B tree after inserting all the elements is achieved.

Example

// Insert the value
void insertion(int item) {
   int flag, i;
   struct btreeNode *child;
   flag = setNodeValue(item, &i, root, &child);
   if (flag)
      root = createNode(i, child);
}

Deletion

The deletion operation in a B tree is slightly different from the deletion operation of a Binary Search Tree. The procedure to delete a node from a B tree is as follows −

Case 1 − If the key to be deleted is in a leaf node and the deletion does not violate the minimum key property, just delete the node.

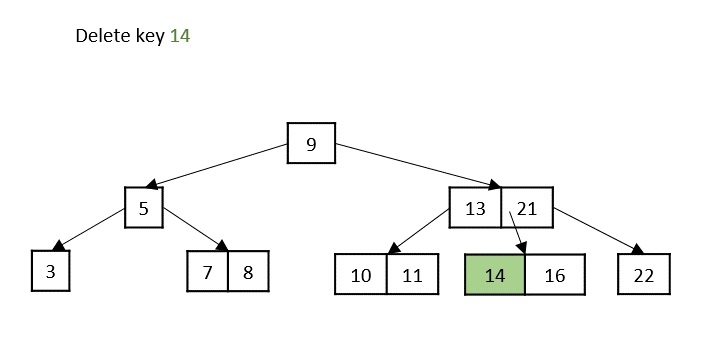
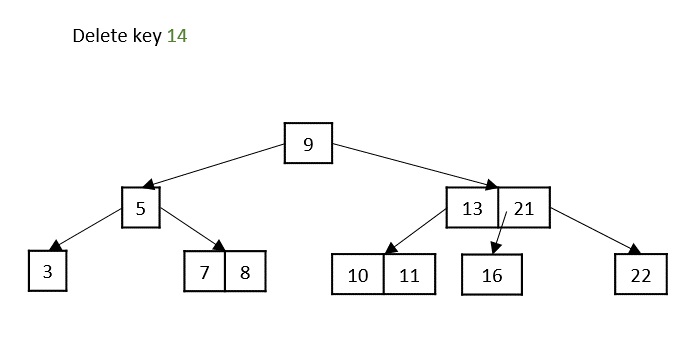
Case 2 − If the key to be deleted is in a leaf node but the deletion violates the minimum key property, borrow a key from either its left sibling or right sibling. In case if both siblings have exact minimum number of keys, merge the node in either of them.

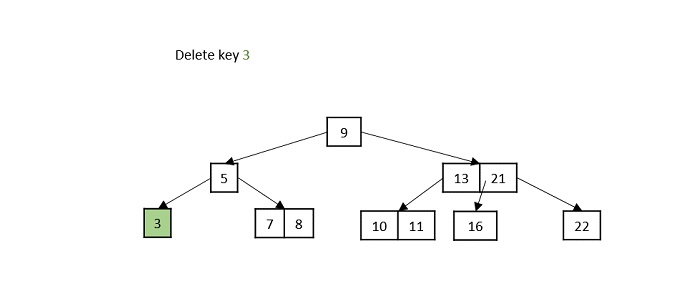
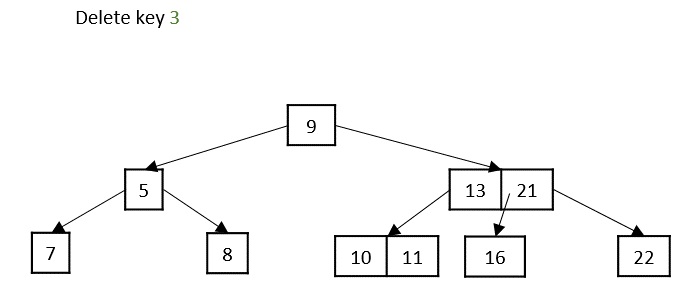
Case 3 − If the key to be deleted is in an internal node, it is replaced by a key in either left child or right child based on which child has more keys. But if both child nodes have minimum number of keys, they’re merged together.

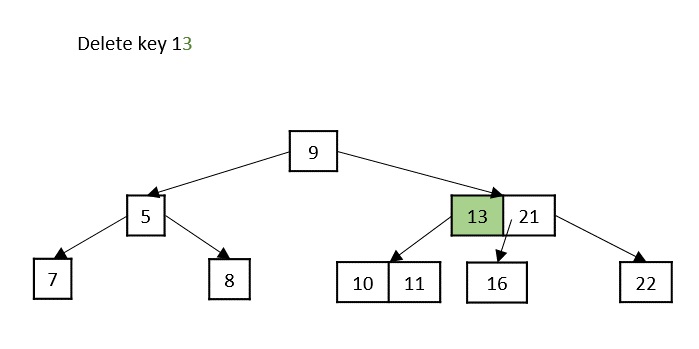
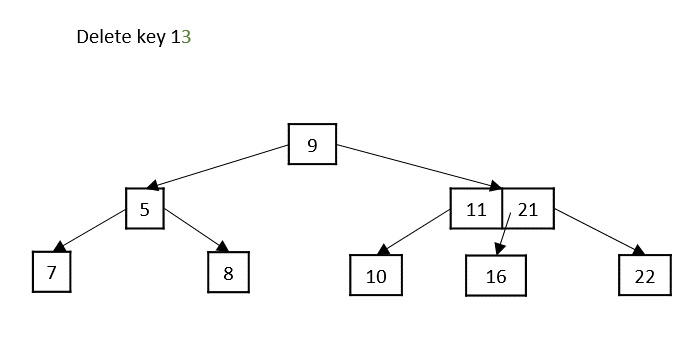
Case 4 − If the key to be deleted is in an internal node violating the minimum keys property, and both its children and sibling have minimum number of keys, merge the children. Then merge its sibling with its parent.

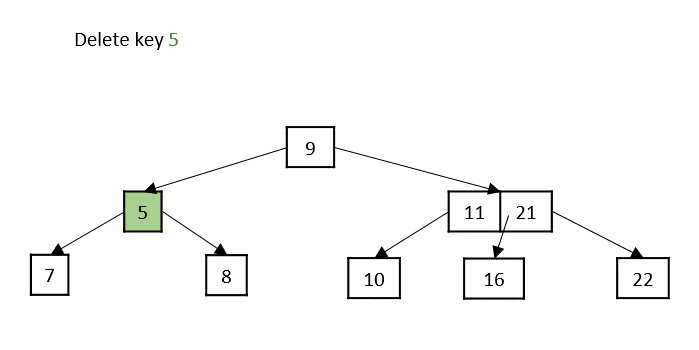
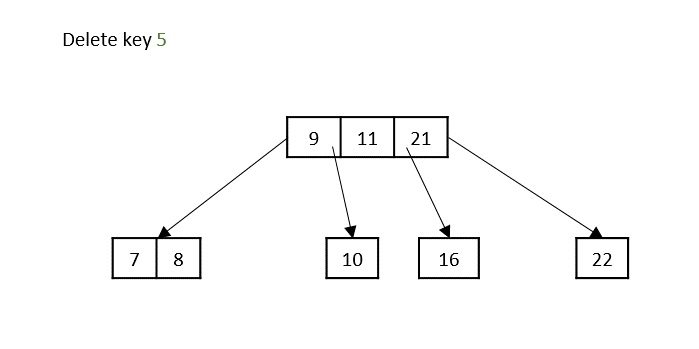
Following is functional C++ code snippet of the deletion operation in B Trees −

// Deletion operation
void deletion(int key){
   int index = searchkey(key);
   if (index < n && keys[index] == key) {
      if (leaf)
         deletion_at_leaf(index);
      else
         deletion_at_nonleaf(index);
   } else {
      if (leaf) {
         cout << "key " << key << " does not exist in the tree\n";
         return;
      }
      bool flag = ((index == n) ? true : false);
      if (C[index]->n < t)
         fill(index);
      if (flag && index > n)
         C[index - 1]->deletion(key);
      else
         C[index]->deletion(key);
   }
   return;
}

// Deletion at the leaf nodes
void deletion_at_leaf(int index){
   for (int i = index + 1; i < n; ++i)
      keys[i - 1] = keys[i];
   n--;
   return;
}

// Deletion at the non leaf node
void deletion_at_nonleaf(int index){
   int key = keys[index];
   if (C[index]->n >= t) {
      int pred = get_Predecessor(index);
      keys[index] = pred;
      C[index]->deletion(pred);
   } else if (C[index + 1]->n >= t) {
      int successor = copysuccessoressor(index);
      keys[index] = successor;
      C[index + 1]->deletion(successor);
   } else {
      merge(index);
      C[index]->deletion(key);
   }
   return;
}

C++ Implementation

Following is the complete implementation of B Trees in C++ −

#include<iostream>
using namespace std;
struct BTree {//node declaration
   int *d;
   BTree **child_ptr;
   bool l;
   int n;
}*r = NULL, *np = NULL, *x = NULL;

BTree* init() {//creation of node
   int i;
   np = new BTree;
   np->d = new int[6];//order 6
   np->child_ptr = new BTree *[7];
   np->l = true;
   np->n = 0;
   for (i = 0; i < 7; i++) {
      np->child_ptr[i] = NULL;
   }
   return np;
}

void traverse(BTree *p) { //traverse the tree
   cout<<endl;
   int i;
   for (i = 0; i < p->n; i++) {
      if (p->l == false) {
         traverse(p->child_ptr[i]);
      }
      cout << " " << p->d[i];
   }
   if (p->l == false) {
      traverse(p->child_ptr[i]);
   }
   cout<<endl;
}

void sort(int *p, int n){ //sort the tree
   int i, j, t;
   for (i = 0; i < n; i++) {
      for (j = i; j <= n; j++) {
         if (p[i] >p[j]) {
            t = p[i];
            p[i] = p[j];
            p[j] = t;
         }
      }
   }
}

int split_child(BTree *x, int i) {
   int j, mid;
   BTree *np1, *np3, *y;
   np3 = init();//create new node
   np3->l = true;
   if (i == -1) {
      mid = x->d[2];//find mid
      x->d[2] = 0;
      x->n--;
      np1 = init();
      np1->l= false;
      x->l= true;
      for (j = 3; j < 6; j++) {
         np3->d[j - 3] = x->d[j];
         np3->child_ptr[j - 3] = x->child_ptr[j];
         np3->n++;
         x->d[j] = 0;
         x->n--;
      }
      for (j = 0; j < 6; j++) {
         x->child_ptr[j] = NULL;
      }
      np1->d[0] = mid;
      np1->child_ptr[np1->n] = x;
      np1->child_ptr[np1->n + 1] = np3;
      np1->n++;
      r = np1;
   } else {
      y = x->child_ptr[i];
      mid = y->d[2];
      y->d[2] = 0;
      y->n--;
      for (j = 3; j <6 ; j++) {
         np3->d[j - 3] = y->d[j];
         np3->n++;
         y->d[j] = 0;
         y->n--;
      }
      x->child_ptr[i + 1] = y;
      x->child_ptr[i + 1] = np3;
   }
   return mid;
}

void insert(int a) {
   int i, t;
   x = r;
   if (x == NULL) {
      r = init();
      x = r;
   } else {
      if (x->l== true && x->n == 6) {
         t = split_child(x, -1);
         x = r;
         for (i = 0; i < (x->n); i++) {
            if ((a >x->d[i]) && (a < x->d[i + 1])) {
               i++;
               break;
            } else if (a < x->d[0]) {
               break;
            } else {
               continue;
            }
         }
         x = x->child_ptr[i];
      } else {
         while (x->l == false) {
            for (i = 0; i < (x->n); i++) {
               if ((a >x->d[i]) && (a < x->d[i + 1])) {
                  i++;
                  break;
               } else if (a < x->d[0]) {
                  break;
               } else {
                  continue;
               }
            }
            if ((x->child_ptr[i])->n == 6) {
               t = split_child(x, i);
               x->d[x->n] = t;
               x->n++;
               continue;
            } else {
               x = x->child_ptr[i];
            }
         }
      }
   }
   x->d[x->n] = a;
   sort(x->d, x->n);
   x->n++;
}

int main() {
   int i, n, t;
   insert(10);
   insert(20);
   insert(30);
   insert(40);
   insert(50);
   cout<<"B tree:\n";
   traverse(r);
}

Output

B tree:
10 20 30 40 50