
- Data Structures & Algorithms
- DSA - Home
- DSA - Overview
- DSA - Environment Setup
- Algorithm
- DSA - Algorithms Basics
- DSA - Asymptotic Analysis
- DSA - Greedy Algorithms
- DSA - Divide and Conquer
- DSA - Dynamic Programming
- Data Structures
- DSA - Data Structure Basics
- DSA - Data Structures and Types
- DSA - Array Data Structure
- Linked Lists
- DSA - Linked List Basics
- DSA - Doubly Linked List
- DSA - Circular Linked List
- Stack & Queue
- DSA - Stack
- DSA - Expression Parsing
- DSA - Queue
- Searching Techniques
- DSA - Linear Search
- DSA - Binary Search
- DSA - Interpolation Search
- DSA - Hash Table
- Sorting Techniques
- DSA - Sorting Algorithms
- DSA - Bubble Sort
- DSA - Insertion Sort
- DSA - Selection Sort
- DSA - Merge Sort
- DSA - Shell Sort
- DSA - Quick Sort
- Graph Data Structure
- DSA - Graph Data Structure
- DSA - Depth First Traversal
- DSA - Breadth First Traversal
- Tree Data Structure
- DSA - Tree Data Structure
- DSA - Tree Traversal
- DSA - Binary Search Tree
- DSA - AVL Tree
- DSA - Red Black Trees
- DSA - B Trees
- DSA - B+ Trees
- DSA - Splay Trees
- DSA - Spanning Tree
- DSA - Tries
- DSA - Heap
- Recursion
- DSA - Recursion Basics
- DSA - Tower of Hanoi
- DSA - Fibonacci Series
- DSA Useful Resources
- DSA - Questions and Answers
- DSA - Quick Guide
- DSA - Useful Resources
- DSA - Discussion
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Data Structure and Algorithms - Queue
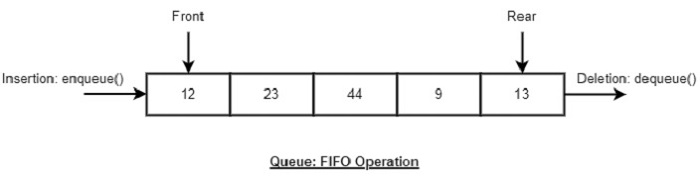
Queue, like Stack, is also an abstract data structure. The thing that makes queue different from stack is that a queue is open at both its ends. Hence, it follows FIFO (First-In-First-Out) structure, i.e. the data item inserted first will also be accessed first. The data is inserted into the queue through one end and deleted from it using the other end.
A real-world example of queue can be a single-lane one-way road, where the vehicle enters first, exits first. More real-world examples can be seen as queues at the ticket windows and bus-stops.
Representation of Queues
Similar to the stack ADT, a queue ADT can also be implemented using arrays, linked lists, or pointers. As a small example in this tutorial, we implement queues using a one-dimensional array.
Basic Operations
Queue operations also include initialization of a queue, usage and permanently deleting the data from the memory.
The most fundamental operations in the queue ADT include: enqueue(), dequeue(), peek(), isFull(), isEmpty(). These are all built-in operations to carry out data manipulation and to check the status of the queue.
Queue uses two pointers − front and rear. The front pointer accesses the data from the front end (helping in enqueueing) while the rear pointer accesses data from the rear end (helping in dequeuing).
Insertion operation: enqueue()
The enqueue() is a data manipulation operation that is used to insert elements into the stack. The following algorithm describes the enqueue() operation in a simpler way.
Algorithm
1 − START 2 – Check if the queue is full. 3 − If the queue is full, produce overflow error and exit. 4 − If the queue is not full, increment rear pointer to point the next empty space. 5 − Add data element to the queue location, where the rear is pointing. 6 − return success. 7 – END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
return itemCount == MAX;
}
bool isEmpty(){
return itemCount == 0;
}
int removeData(){
int data = intArray[front++];
if(front == MAX) {
front = 0;
}
itemCount--;
return data;
}
void insert(int data){
if(!isFull()) {
if(rear == MAX-1) {
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
int main(){
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
insert(15);
printf("Queue: ");
while(!isEmpty()) {
int n = removeData();
printf("%d ",n);
}
}
Output
Queue: 3 5 9 1 12 15
#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
return itemCount == MAX;
}
bool isEmpty(){
return itemCount == 0;
}
int removeData(){
int data = intArray[front++];
if(front == MAX) {
front = 0;
}
itemCount--;
return data;
}
void insert(int data){
if(!isFull()) {
if(rear == MAX-1) {
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
int main(){
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
insert(15);
printf("Queue: ");
while(!isEmpty()) {
int n = removeData();
printf("%d ",n);
}
}
Output
Queue: 3 5 9 1 12 15
import java.util.LinkedList;
import java.util.Queue;
public class QueueExample {
public static void main(String[] args) {
Queue<Integer> q = new LinkedList<>();
q.add(6);
q.add(1);
q.add(8);
q.add(4);
q.add(7);
System.out.println("The queue is: " + q);
}
}
Output
The queue is: [6, 1, 8, 4, 7]
class Queue:
def __init__(self):
self.queue = list()
def __str__(self):
return str(self.queue)
def addtoqueue(self,data):
# Insert method to add element
if data not in self.queue:
self.queue.insert(0,data)
return True
return False
q = Queue()
q.addtoqueue("36")
q.addtoqueue("24")
q.addtoqueue("48")
q.addtoqueue("12")
q.addtoqueue("66")
print("Queue:")
print(q)
Output
Queue: ['66', '12', '48', '24', '36']
Deletion Operation: dequeue()
The dequeue() is a data manipulation operation that is used to remove elements from the stack. The following algorithm describes the dequeue() operation in a simpler way.
Algorithm
1 – START 2 − Check if the queue is empty. 3 − If the queue is empty, produce underflow error and exit. 4 − If the queue is not empty, access the data where front is pointing. 5 − Increment front pointer to point to the next available data element. 6 − Return success. 7 – END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
return itemCount == MAX;
}
bool isEmpty(){
return itemCount == 0;
}
void insert(int data){
if(!isFull()) {
if(rear == MAX-1) {
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
int removeData(){
int data = intArray[front++];
if(front == MAX) {
front = 0;
}
itemCount--;
return data;
}
int main(){
int i;
/* insert 5 items */
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
insert(15);
printf("Queue: ");
for(i = 0; i < MAX; i++)
printf("%d ", intArray[i]);
// remove one item
int num = removeData();
printf("\nElement removed: %d\n",num);
printf("Updated Queue: ");
while(!isEmpty()) {
int n = removeData();
printf("%d ",n);
}
}
Output
Queue: 3 5 9 1 12 15 Element removed: 3 Updated Queue: 5 9 1 12 15
#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
return itemCount == MAX;
}
bool isEmpty(){
return itemCount == 0;
}
void insert(int data){
if(!isFull()) {
if(rear == MAX-1) {
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
int removeData(){
int data = intArray[front++];
if(front == MAX) {
front = 0;
}
itemCount--;
return data;
}
int main(){
int i;
/* insert 5 items */
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
insert(15);
printf("Queue: ");
for(i = 0; i < MAX; i++)
printf("%d ", intArray[i]);
// remove one item
int num = removeData();
printf("\nElement removed: %d\n",num);
printf("Updated Queue: ");
while(!isEmpty()) {
int n = removeData();
printf("%d ",n);
}
}
Output
Queue: 3 5 9 1 12 15 Element removed: 3 Updated Queue: 5 9 1 12 15
import java.util.LinkedList;
import java.util.Queue;
public class QueueExample {
public static void main(String[] args) {
Queue<Integer> q = new LinkedList<>();
q.add(6);
q.add(1);
q.add(8);
q.add(4);
q.add(7);
System.out.println("The queue is: " + q);
int n = q.remove();
System.out.println("The element deleted is: " + n);
System.out.println("Queue after deletion: " + q);
}
}
Output
The queue is: [6, 1, 8, 4, 7] The element deleted is: 6 Queue after deletion: [1, 8, 4, 7]
class Queue:
def __init__(self):
self.queue = list()
def __str__(self):
return str(self.queue)
def addtoqueue(self,data):
# Insert method to add element
if data not in self.queue:
self.queue.insert(0,data)
return True
return False
def removefromqueue(self):
if len(self.queue)>0:
return self.queue.pop()
return ("Queue is empty")
q = Queue()
q.addtoqueue("36")
q.addtoqueue("24")
q.addtoqueue("48")
q.addtoqueue("12")
q.addtoqueue("66")
print("Queue:")
print(q)
print("Element deleted from queue: ",q.removefromqueue())
Output
Queue: ['66', '12', '48', '24', '36'] Element deleted from queue: 36
The peek() Operation
The peek() is an operation which is used to retrieve the frontmost element in the queue, without deleting it. This operation is used to check the status of the queue with the help of the pointer.
Algorithm
1 – START 2 – Return the element at the front of the queue 3 – END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
return intArray[front];
}
bool isFull(){
return itemCount == MAX;
}
void insert(int data){
if(!isFull()) {
if(rear == MAX-1) {
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
int main(){
int i;
/* insert 5 items */
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
insert(15);
printf("Queue: ");
for(i = 0; i < MAX; i++)
printf("%d ", intArray[i]);
printf("\nElement at front: %d\n",peek());
}
Output
Queue: 3 5 9 1 12 15 Element at front: 3
#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
return intArray[front];
}
bool isFull(){
return itemCount == MAX;
}
void insert(int data){
if(!isFull()) {
if(rear == MAX-1) {
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
int main(){
int i;
/* insert 5 items */
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
insert(15);
printf("Queue: ");
for(i = 0; i < MAX; i++)
printf("%d ", intArray[i]);
printf("\nElement at front: %d\n",peek());
}
Output
Queue: 3 5 9 1 12 15 Element at front: 3
import java.util.LinkedList;
import java.util.Queue;
public class QueueExample {
public static void main(String[] args) {
Queue<Integer> q = new LinkedList<>();
q.add(6);
q.add(1);
q.add(8);
q.add(4);
q.add(7);
System.out.println("The queue is: " + q);
}
}
Output
The queue is: [6, 1, 8, 4, 7]
class Queue:
def __init__(self):
self.queue = list()
def __str__(self):
return str(self.queue)
def addtoqueue(self,data):
# Insert method to add element
if data not in self.queue:
self.queue.insert(0,data)
return True
return False
def peek(self):
return self.queue[-1]
q = Queue()
q.addtoqueue("36")
q.addtoqueue("24")
q.addtoqueue("48")
q.addtoqueue("12")
q.addtoqueue("66")
print("Queue:")
print(q)
print("The frontmost element of the queue: ",q.peek())
Output
Queue: ['66', '12', '48', '24', '36'] The frontmost element of the queue: 36
The isFull() Operation
The isFull() operation verifies whether the stack is full.
Algorithm
1 – START 2 – If the count of queue elements equals the queue size, return true 3 – Otherwise, return false 4 – END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
return itemCount == MAX;
}
void insert(int data){
if(!isFull()) {
if(rear == MAX-1) {
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
int main(){
int i;
/* insert 5 items */
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
insert(15);
printf("Queue: ");
for(i = 0; i < MAX; i++)
printf("%d ", intArray[i]);
printf("\n");
if(isFull()) {
printf("Queue is full!\n");
}
}
Output
Queue: 3 5 9 1 12 15 Queue is full!
#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
return itemCount == MAX;
}
void insert(int data){
if(!isFull()) {
if(rear == MAX-1) {
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
int main(){
int i;
/* insert 5 items */
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
insert(15);
printf("Queue: ");
for(i = 0; i < MAX; i++)
printf("%d ", intArray[i]);
printf("\n");
if(isFull()) {
printf("Queue is full!\n");
}
}
Output
Queue: 3 5 9 1 12 15 Queue is full!
import java.io.*;
public class QueueExample {
private int intArray[];
private int front;
private int rear;
private int itemCount;
private int MAX;
QueueExample(int size) {
intArray = new int[size];
front = 0;
rear = -1;
MAX = size;
itemCount = 0;
}
public boolean isFull() {
return itemCount == MAX;
}
public void insert(int key) {
if(!isFull()) {
if(rear == MAX-1) {
rear = -1;
}
intArray[++rear] = key;
itemCount++;
}
}
public static void main (String[] args) {
QueueExample q = new QueueExample(5);
q.insert(1); // inserting 1 in the stack
q.insert(2);
q.insert(3);
q.insert(4);
q.insert(5);
System.out.println("Stack Full? " + q.isFull());
}
}
Output
Stack Full? true
The isEmpty() operation
The isEmpty() operation verifies whether the stack is empty. This operation is used to check the status of the stack with the help of top pointer.
Algorithm
1 – START 2 – If the count of queue elements equals zero, return true 3 – Otherwise, return false 4 – END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isEmpty(){
return itemCount == 0;
}
int main(){
int i;
printf("Queue: ");
for(i = 0; i < MAX; i++)
printf("%d ", intArray[i]);
printf("\n");
if(isEmpty()) {
printf("Queue is Empty!\n");
}
}
Output
Queue: 0 0 0 0 0 0 Queue is Empty!
#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isEmpty(){
return itemCount == 0;
}
int main(){
int i;
printf("Queue: ");
for(i = 0; i < MAX; i++)
printf("%d ", intArray[i]);
printf("\n");
if(isEmpty()) {
printf("Queue is Empty!\n");
}
}
Output
Queue: 0 0 0 0 0 0 Queue is Empty!
import java.io.*;
public class QueueExample {
private int intArray[];
private int front;
private int rear;
private int itemCount;
private int MAX;
QueueExample(int size) {
intArray = new int[size];
front = 0;
rear = -1;
MAX = size;
itemCount = 0;
}
public boolean isEmpty() {
return itemCount == 0;
}
public static void main (String[] args) {
QueueExample q = new QueueExample(5);
System.out.println("Stack Empty? " + q.isEmpty());
}
}
Output
Stack Empty? true
Implementation of Queue
In this chapter, the algorithm implementation of the Queue data structure is performed in four programming languages.
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
return intArray[front];
}
bool isEmpty(){
return itemCount == 0;
}
bool isFull(){
return itemCount == MAX;
}
int size(){
return itemCount;
}
void insert(int data){
if(!isFull()) {
if(rear == MAX-1) {
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
int removeData(){
int data = intArray[front++];
if(front == MAX) {
front = 0;
}
itemCount--;
return data;
}
int main(){
/* insert 5 items */
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
// front : 0
// rear : 4
// ------------------
// index : 0 1 2 3 4
// ------------------
// queue : 3 5 9 1 12
insert(15);
// front : 0
// rear : 5
// ---------------------
// index : 0 1 2 3 4 5
// ---------------------
// queue : 3 5 9 1 12 15
if(isFull()) {
printf("Queue is full!\n");
}
// remove one item
int num = removeData();
printf("Element removed: %d\n",num);
// front : 1
// rear : 5
// -------------------
// index : 1 2 3 4 5
// -------------------
// queue : 5 9 1 12 15
// insert more items
insert(16);
// front : 1
// rear : -1
// ----------------------
// index : 0 1 2 3 4 5
// ----------------------
// queue : 16 5 9 1 12 15
// As queue is full, elements will not be inserted.
insert(17);
insert(18);
// ----------------------
// index : 0 1 2 3 4 5
// ----------------------
// queue : 16 5 9 1 12 15
printf("Element at front: %d\n",peek());
printf("----------------------\n");
printf("index : 5 4 3 2 1 0\n");
printf("----------------------\n");
printf("Queue: ");
while(!isEmpty()) {
int n = removeData();
printf("%d ",n);
}
}
Output
Queue is full! Element removed: 3 Element at front: 5 ---------------------- index : 5 4 3 2 1 0 ---------------------- Queue: 5 9 1 12 15 16
#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
return intArray[front];
}
bool isEmpty(){
return itemCount == 0;
}
bool isFull(){
return itemCount == MAX;
}
int size(){
return itemCount;
}
void insert(int data){
if(!isFull()) {
if(rear == MAX-1) {
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
int removeData(){
int data = intArray[front++];
if(front == MAX) {
front = 0;
}
itemCount--;
return data;
}
int main(){
/* insert 5 items */
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
// front : 0
// rear : 4
// ------------------
// index : 0 1 2 3 4
// ------------------
// queue : 3 5 9 1 12
insert(15);
// front : 0
// rear : 5
// ---------------------
// index : 0 1 2 3 4 5
// ---------------------
// queue : 3 5 9 1 12 15
if(isFull()) {
printf("Queue is full!\n");
}
// remove one item
int num = removeData();
printf("Element removed: %d\n",num);
// front : 1
// rear : 5
// -------------------
// index : 1 2 3 4 5
// -------------------
// queue : 5 9 1 12 15
// insert more items
insert(16);
// front : 1
// rear : -1
// ----------------------
// index : 0 1 2 3 4 5
// ----------------------
// queue : 16 5 9 1 12 15
// As queue is full, elements will not be inserted.
insert(17);
insert(18);
// ----------------------
// index : 0 1 2 3 4 5
// ----------------------
// queue : 16 5 9 1 12 15
printf("Element at front: %d\n",peek());
printf("----------------------\n");
printf("index : 5 4 3 2 1 0\n");
printf("----------------------\n");
printf("Queue: ");
while(!isEmpty()) {
int n = removeData();
printf("%d ",n);
}
}
Output
Queue is full! Element removed: 3 Element at front: 5 ---------------------- index : 5 4 3 2 1 0 ---------------------- Queue: 5 9 1 12 15 16
import java.util.LinkedList;
import java.util.Queue;
public class QueueExample {
public static void main(String[] args) {
Queue<Integer> q = new LinkedList<>();
q.add(6);
q.add(1);
q.add(8);
q.add(4);
q.add(7);
System.out.println("The queue is: " + q);
int n = q.remove();
System.out.println("The element deleted is: " + n);
System.out.println("Queue after deletion: " + q);
int size = q.size();
System.out.println("Size of the queue is: " + size);
}
}
Output
The queue is: [6, 1, 8, 4, 7]The element deleted is: 6 Queue after deletion: [1, 8, 4, 7] Size of the queue is: 4
class Queue:
def __init__(self):
self.queue = list()
def addtoqueue(self,data):
# Insert method to add element
if data not in self.queue:
self.queue.insert(0,data)
return True
return False
def size(self):
return len(self.queue)
def removefromqueue(self):
if len(self.queue)>0:
return self.queue.pop()
return ("Queue is empty")
q = Queue()
q.addtoqueue("36")
q.addtoqueue("24")
q.addtoqueue("48")
q.addtoqueue("12")
q.addtoqueue("66")
print("size of the queue: ",q.size())
print("Element deleted from queue: ",q.removefromqueue())
print("size of the queue after deletion: ",q.size())
Output
size of the queue: 5 Element deleted from queue: 36 size of the queue after deletion: 4