Data Structures & Algorithms - Quick Guide

Data Structures & Algorithms - Overview

Data Structure is a systematic way to organize data in order to use it efficiently. Following terms are the foundation terms of a data structure.

Interface − Each data structure has an interface. Interface represents the set of operations that a data structure supports. An interface only provides the list of supported operations, type of parameters they can accept and return type of these operations.
Implementation − Implementation provides the internal representation of a data structure. Implementation also provides the definition of the algorithms used in the operations of the data structure.

Characteristics of a Data Structure

Correctness − Data structure implementation should implement its interface correctly.
Time Complexity − Running time or the execution time of operations of data structure must be as small as possible.
Space Complexity − Memory usage of a data structure operation should be as little as possible.

Need for Data Structure

As applications are getting complex and data rich, there are three common problems that applications face now-a-days.

Data Search − Consider an inventory of 1 million(10⁶) items of a store. If the application is to search an item, it has to search an item in 1 million(10⁶) items every time slowing down the search. As data grows, search will become slower.
Processor speed − Processor speed although being very high, falls limited if the data grows to billion records.
Multiple requests − As thousands of users can search data simultaneously on a web server, even the fast server fails while searching the data.

To solve the above-mentioned problems, data structures come to rescue. Data can be organized in a data structure in such a way that all items may not be required to be searched, and the required data can be searched almost instantly.

Execution Time Cases

There are three cases which are usually used to compare various data structure's execution time in a relative manner.

Worst Case − This is the scenario where a particular data structure operation takes maximum time it can take. If an operation's worst case time is ƒ(n) then this operation will not take more than ƒ(n) time where ƒ(n) represents function of n.
Average Case − This is the scenario depicting the average execution time of an operation of a data structure. If an operation takes ƒ(n) time in execution, then m operations will take mƒ(n) time.
Best Case − This is the scenario depicting the least possible execution time of an operation of a data structure. If an operation takes ƒ(n) time in execution, then the actual operation may take time as the random number which would be maximum as ƒ(n).

Basic Terminology

Data − Data are values or set of values.
Data Item − Data item refers to single unit of values.
Group Items − Data items that are divided into sub items are called as Group Items.
Elementary Items − Data items that cannot be divided are called as Elementary Items.
Attribute and Entity − An entity is that which contains certain attributes or properties, which may be assigned values.
Entity Set − Entities of similar attributes form an entity set.
Field − Field is a single elementary unit of information representing an attribute of an entity.
Record − Record is a collection of field values of a given entity.
File − File is a collection of records of the entities in a given entity set.

Data Structures - Environment Setup

Local Environment Setup

If you are still willing to set up your environment for C programming language, you need the following two tools available on your computer, (a) Text Editor and (b) The C Compiler.

Text Editor

This will be used to type your program. Examples of few editors include Windows Notepad, OS Edit command, Brief, Epsilon, EMACS, and vim or vi.

The name and the version of the text editor can vary on different operating systems. For example, Notepad will be used on Windows, and vim or vi can be used on Windows as well as Linux or UNIX.

The files you create with your editor are called source files and contain program source code. The source files for C programs are typically named with the extension ".c".

Before starting your programming, make sure you have one text editor in place and you have enough experience to write a computer program, save it in a file, compile it, and finally execute it.

The C Compiler

The source code written in the source file is the human readable source for your program. It needs to be "compiled", to turn into machine language so that your CPU can actually execute the program as per the given instructions.

This C programming language compiler will be used to compile your source code into a final executable program. We assume you have the basic knowledge about a programming language compiler.

Most frequently used and free available compiler is GNU C/C++ compiler. Otherwise, you can have compilers either from HP or Solaris if you have respective Operating Systems (OS).

The following section guides you on how to install GNU C/C++ compiler on various OS. We are mentioning C/C++ together because GNU GCC compiler works for both C and C++ programming languages.

Installation on UNIX/Linux

If you are using Linux or UNIX, then check whether GCC is installed on your system by entering the following command from the command line −

$ gcc -v

If you have GNU compiler installed on your machine, then it should print a message such as the following −

Using built-in specs.
Target: i386-redhat-linux
Configured with: ../configure --prefix = /usr .......
Thread model: posix
gcc version 4.1.2 20080704 (Red Hat 4.1.2-46)

If GCC is not installed, then you will have to install it yourself using the detailed instructions available at https://gcc.gnu.org/install/

This tutorial has been written based on Linux and all the given examples have been compiled on Cent OS flavor of Linux system.

Installation on Mac OS

If you use Mac OS X, the easiest way to obtain GCC is to download the Xcode development environment from Apple's website and follow the simple installation instructions. Once you have Xcode setup, you will be able to use GNU compiler for C/C++.

Xcode is currently available at developer.apple.com/technologies/tools/

Installation on Windows

To install GCC on Windows, you need to install MinGW. To install MinGW, go to the MinGW homepage, www.mingw.org, and follow the link to the MinGW download page. Download the latest version of the MinGW installation program, which should be named MinGW-<version>.exe.

While installing MinWG, at a minimum, you must install gcc-core, gcc-g++, binutils, and the MinGW runtime, but you may wish to install more.

Add the bin subdirectory of your MinGW installation to your PATH environment variable, so that you can specify these tools on the command line by their simple names.

When the installation is complete, you will be able to run gcc, g++, ar, ranlib, dlltool, and several other GNU tools from the Windows command line.

Data Structures - Algorithms Basics

Algorithm is a step-by-step procedure, which defines a set of instructions to be executed in a certain order to get the desired output. Algorithms are generally created independent of underlying languages, i.e. an algorithm can be implemented in more than one programming language.

From the data structure point of view, following are some important categories of algorithms −

Search − Algorithm to search an item in a data structure.
Sort − Algorithm to sort items in a certain order.
Insert − Algorithm to insert item in a data structure.
Update − Algorithm to update an existing item in a data structure.
Delete − Algorithm to delete an existing item from a data structure.

Characteristics of an Algorithm

Not all procedures can be called an algorithm. An algorithm should have the following characteristics −

Unambiguous − Algorithm should be clear and unambiguous. Each of its steps (or phases), and their inputs/outputs should be clear and must lead to only one meaning.
Input − An algorithm should have 0 or more well-defined inputs.
Output − An algorithm should have 1 or more well-defined outputs, and should match the desired output.
Finiteness − Algorithms must terminate after a finite number of steps.
Feasibility − Should be feasible with the available resources.
Independent − An algorithm should have step-by-step directions, which should be independent of any programming code.

How to Write an Algorithm?

There are no well-defined standards for writing algorithms. Rather, it is problem and resource dependent. Algorithms are never written to support a particular programming code.

As we know that all programming languages share basic code constructs like loops (do, for, while), flow-control (if-else), etc. These common constructs can be used to write an algorithm.

We write algorithms in a step-by-step manner, but it is not always the case. Algorithm writing is a process and is executed after the problem domain is well-defined. That is, we should know the problem domain, for which we are designing a solution.

Example

Let's try to learn algorithm-writing by using an example.

Problem − Design an algorithm to add two numbers and display the result.

Step 1 − START
Step 2 − declare three integers a, b & c
Step 3 − define values of a & b
Step 4 − add values of a & b
Step 5 − store output of step 4 to c
Step 6 − print c
Step 7 − STOP

Algorithms tell the programmers how to code the program. Alternatively, the algorithm can be written as −

Step 1 − START ADD
Step 2 − get values of a & b
Step 3 − c ← a + b
Step 4 − display c
Step 5 − STOP

In design and analysis of algorithms, usually the second method is used to describe an algorithm. It makes it easy for the analyst to analyze the algorithm ignoring all unwanted definitions. He can observe what operations are being used and how the process is flowing.

Writing step numbers, is optional.

We design an algorithm to get a solution of a given problem. A problem can be solved in more than one ways.

Hence, many solution algorithms can be derived for a given problem. The next step is to analyze those proposed solution algorithms and implement the best suitable solution.

Algorithm Analysis

Efficiency of an algorithm can be analyzed at two different stages, before implementation and after implementation. They are the following −

A Priori Analysis − This is a theoretical analysis of an algorithm. Efficiency of an algorithm is measured by assuming that all other factors, for example, processor speed, are constant and have no effect on the implementation.
A Posterior Analysis − This is an empirical analysis of an algorithm. The selected algorithm is implemented using programming language. This is then executed on target computer machine. In this analysis, actual statistics like running time and space required, are collected.

We shall learn about a priori algorithm analysis. Algorithm analysis deals with the execution or running time of various operations involved. The running time of an operation can be defined as the number of computer instructions executed per operation.

Algorithm Complexity

Suppose X is an algorithm and n is the size of input data, the time and space used by the algorithm X are the two main factors, which decide the efficiency of X.

Time Factor − Time is measured by counting the number of key operations such as comparisons in the sorting algorithm.
Space Factor − Space is measured by counting the maximum memory space required by the algorithm.

The complexity of an algorithm f(n) gives the running time and/or the storage space required by the algorithm in terms of n as the size of input data.

Space Complexity

Space complexity of an algorithm represents the amount of memory space required by the algorithm in its life cycle. The space required by an algorithm is equal to the sum of the following two components −

A fixed part that is a space required to store certain data and variables, that are independent of the size of the problem. For example, simple variables and constants used, program size, etc.
A variable part is a space required by variables, whose size depends on the size of the problem. For example, dynamic memory allocation, recursion stack space, etc.

Space complexity S(P) of any algorithm P is S(P) = C + SP(I), where C is the fixed part and S(I) is the variable part of the algorithm, which depends on instance characteristic I. Following is a simple example that tries to explain the concept −

Algorithm: SUM(A, B)
Step 1 -  START
Step 2 -  C ← A + B + 10
Step 3 -  Stop

Here we have three variables A, B, and C and one constant. Hence S(P) = 1 + 3. Now, space depends on data types of given variables and constant types and it will be multiplied accordingly.

Time Complexity

Time complexity of an algorithm represents the amount of time required by the algorithm to run to completion. Time requirements can be defined as a numerical function T(n), where T(n) can be measured as the number of steps, provided each step consumes constant time.

For example, addition of two n-bit integers takes n steps. Consequently, the total computational time is T(n) = c ∗ n, where c is the time taken for the addition of two bits. Here, we observe that T(n) grows linearly as the input size increases.

Data Structures - Asymptotic Analysis

Asymptotic analysis of an algorithm refers to defining the mathematical foundation/framing of its run-time performance. Using asymptotic analysis, we can very well conclude the best case, average case, and worst case scenario of an algorithm.

Asymptotic analysis is input bound i.e., if there's no input to the algorithm, it is concluded to work in a constant time. Other than the "input" all other factors are considered constant.

Asymptotic analysis refers to computing the running time of any operation in mathematical units of computation. For example, the running time of one operation is computed as f(n) and may be for another operation it is computed as g(n²). This means the first operation running time will increase linearly with the increase in n and the running time of the second operation will increase exponentially when n increases. Similarly, the running time of both operations will be nearly the same if n is significantly small.

Usually, the time required by an algorithm falls under three types −

Best Case − Minimum time required for program execution.
Average Case − Average time required for program execution.
Worst Case − Maximum time required for program execution.

Asymptotic Notations

Following are the commonly used asymptotic notations to calculate the running time complexity of an algorithm.

Ο − Big Oh Notation
Ω − Big Omega Notation
Θ − Theta Notation
o − Little Oh Notation
ω − Little Omega Notation

Big Oh Notation, Ο

The notation Ο(n) is the formal way to express the upper bound of an algorithm's running time. It measures the worst case time complexity or the longest amount of time an algorithm can possibly take to complete.

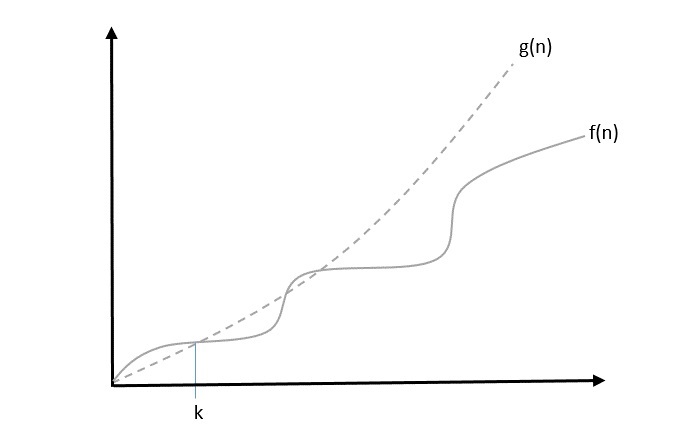
For example, for a function f(n)

Ο(f(n)) = { g(n) : there exists c > 0 and n0 such that g(n) ≤ c.f(n) for all n > n0. }

Example

Let us consider a given function, f(n) = 4.n³+10.n²+5.n+1.

Considering g(n) = n³

f(n) ≥ 5.g(n) for all the values of n > 2.

Hence, the complexity of f(n) can be represented as O (g (n) ) ,i.e. O (n³).

Big Omega Notation, Ω

The notation Ω(n) is the formal way to express the lower bound of an algorithm's running time. It measures the best case time complexity or the best amount of time an algorithm can possibly take to complete.

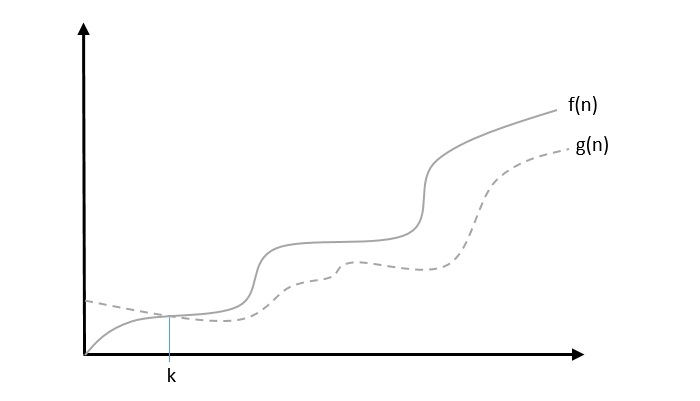
For example, for a function f(n)

Ω(f(n)) ≥ { g(n) : there exists c > 0 and n0 such that g(n) ≤ c.f(n) for all n > n0. }

Example

Let us consider a given function, f(n) = 4.n³+10.n²+5.n+1

Considering g(n) = n³ , f(n) ≥ 4.g(n) for all the values of n > 0.

Hence, the complexity of f(n) can be represented as Ω (g (n) ) ,i.e. Ω (n³).

Theta Notation, θ

The notation θ(n) is the formal way to express both the lower bound and the upper bound of an algorithm's running time. Some may confuse the theta notation as the average case time complexity; while big theta notation could be almost accurately used to describe the average case, other notations could be used as well. It is represented as follows −

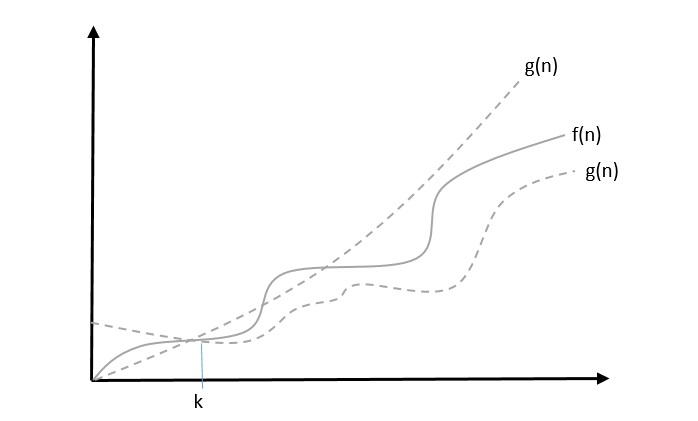
θ(f(n)) = { g(n) if and only if g(n) = Ο(f(n)) and g(n) = Ω(f(n)) for all n > n0. }

Example

Let us consider a given function, f(n) = 4.n³+10.n²+5.n+1

Considering g(n) = n³ , 4.g(n)≤ f(n)≤ 5.g(n) for all the values of n.

Hence, the complexity of f(n) can be represented as Ɵ (g (n) ) ,i.e. Ɵ (n³).

Little Oh (o) and Little Omega (ω) Notations

The Little Oh and Little Omega notations also represent the best and worst case complexities but they are not asymptotically tight in contrast to the Big Oh and Big Omega Notations. Therefore, the most commonly used notations to represent time complexities are Big Oh and Big Omega Notations only.

Common Asymptotic Notations

Following is a list of some common asymptotic notations −

constant	−	O(1)
logarithmic	−	O(log n)
linear	−	O(n)
n log n	−	O(n log n)
quadratic	−	O(n²)
cubic	−	O(n³)
polynomial	−	n^O(1)
exponential	−	2^O(n)

Data Structures - Greedy Algorithms

An algorithm is designed to achieve optimum solution for a given problem. In greedy algorithm approach, decisions are made from the given solution domain. As being greedy, the closest solution that seems to provide an optimum solution is chosen.

Greedy algorithms try to find a localized optimum solution, which may eventually lead to globally optimized solutions. However, generally greedy algorithms do not provide globally optimized solutions.

Counting Coins

This problem is to count to a desired value by choosing the least possible coins and the greedy approach forces the algorithm to pick the largest possible coin. If we are provided coins of € 1, 2, 5 and 10 and we are asked to count € 18 then the greedy procedure will be −

1 − Select one € 10 coin, the remaining count is 8
2 − Then select one € 5 coin, the remaining count is 3
3 − Then select one € 2 coin, the remaining count is 1
4 − And finally, the selection of one € 1 coins solves the problem

Though, it seems to be working fine, for this count we need to pick only 4 coins. But if we slightly change the problem then the same approach may not be able to produce the same optimum result.

For the currency system, where we have coins of 1, 7, 10 value, counting coins for value 18 will be absolutely optimum but for count like 15, it may use more coins than necessary. For example, the greedy approach will use 10 + 1 + 1 + 1 + 1 + 1, total 6 coins. Whereas the same problem could be solved by using only 3 coins (7 + 7 + 1)

Hence, we may conclude that the greedy approach picks an immediate optimized solution and may fail where global optimization is a major concern.

Examples

Most networking algorithms use the greedy approach. Here is a list of few of them −

Travelling Salesman Problem
Prim's Minimal Spanning Tree Algorithm
Kruskal's Minimal Spanning Tree Algorithm
Dijkstra's Minimal Spanning Tree Algorithm
Graph − Map Coloring
Graph − Vertex Cover
Knapsack Problem
Job Scheduling Problem

There are lots of similar problems that uses the greedy approach to find an optimum solution.

Data Structures - Divide and Conquer

To understand the divide and conquer design strategy of algorithms, let us use a simple real world example. Consider an instance where we need to brush a type C curly hair and remove all the knots from it. To do that, the first step is to section the hair in smaller strands to make the combing easier than combing the hair altogether. The same technique is applied on algorithms.

Divide and conquer approach breaks down a problem into multiple sub-problems recursively until it cannot be divided further. These sub-problems are solved first and the solutions are merged together to form the final solution.

The common procedure for the divide and conquer design technique is as follows −

Divide − We divide the original problem into multiple sub-problems until they cannot be divided further.
Conquer − Then these subproblems are solved separately with the help of recursion
Combine − Once solved, all the subproblems are merged/combined together to form the final solution of the original problem.

There are several ways to give input to the divide and conquer algorithm design pattern. Two major data structures used are − arrays and linked lists. Their usage is explained as

Arrays as Input

There are various ways in which various algorithms can take input such that they can be solved using the divide and conquer technique. Arrays are one of them. In algorithms that require input to be in the form of a list, like various sorting algorithms, array data structures are most commonly used.

In the input for a sorting algorithm below, the array input is divided into subproblems until they cannot be divided further.

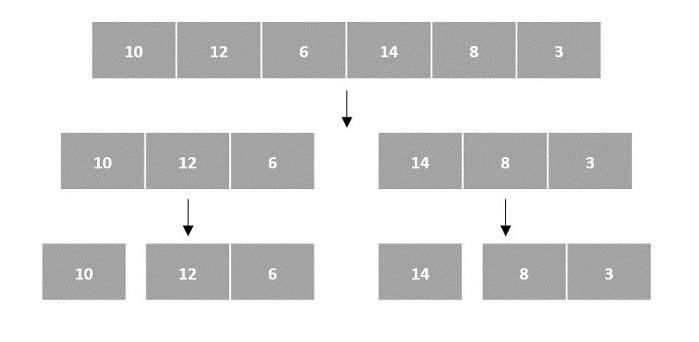
Then, the subproblems are sorted (the conquer step) and are merged to form the solution of the original array back (the combine step).

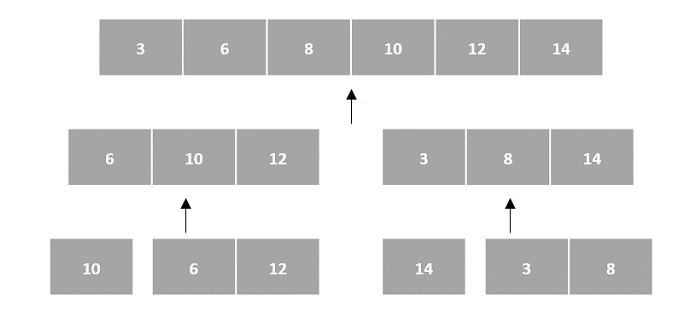
Since arrays are indexed and linear data structures, sorting algorithms most popularly use array data structures to receive input.

Linked Lists as Input

Another data structure that can be used to take input for divide and conquer algorithms is a linked list (for example, merge sort using linked lists). Like arrays, linked lists are also linear data structures that store data sequentially.

Consider the merge sort algorithm on linked list; following the very popular tortoise and hare algorithm, the list is divided until it cannot be divided further.

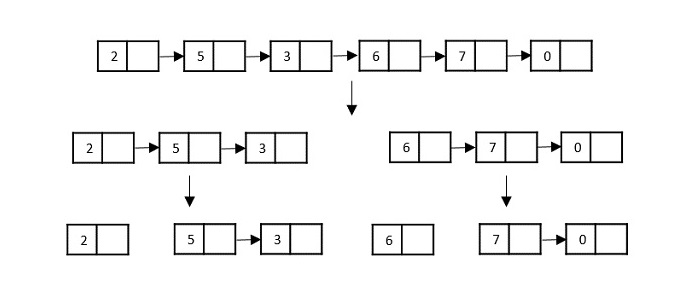
Then, the nodes in the list are sorted (conquered). These nodes are then combined (or merged) in recursively until the final solution is achieved.

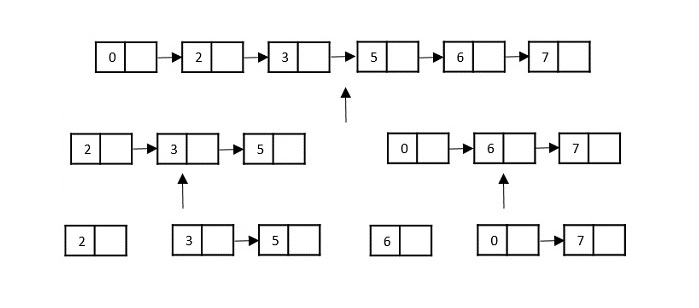
Various searching algorithms can also be performed on the linked list data structures with a slightly different technique as linked lists are not indexed linear data structures. They must be handled using the pointers available in the nodes of the list.

Examples

The following computer algorithms are based on divide-and-conquer programming approach −

Merge Sort
Quick Sort
Binary Search
Strassen's Matrix Multiplication
Closest Pair

There are various ways available to solve any computer problem, but the mentioned are a good example of divide and conquer approach.

Data Structures - Dynamic Programming

Dynamic programming approach is similar to divide and conquer in breaking down the problem into smaller and yet smaller possible sub-problems. But unlike, divide and conquer, these sub-problems are not solved independently. Rather, results of these smaller sub-problems are remembered and used for similar or overlapping sub-problems.

Dynamic programming is used where we have problems, which can be divided into similar sub-problems, so that their results can be re-used. Mostly, these algorithms are used for optimization. Before solving the in-hand sub-problem, dynamic algorithm will try to examine the results of the previously solved sub-problems. The solutions of sub-problems are combined in order to achieve the best solution.

So we can say that −

The problem should be able to be divided into smaller overlapping sub-problem.
An optimum solution can be achieved by using an optimum solution of smaller sub-problems.
Dynamic algorithms use Memoization.

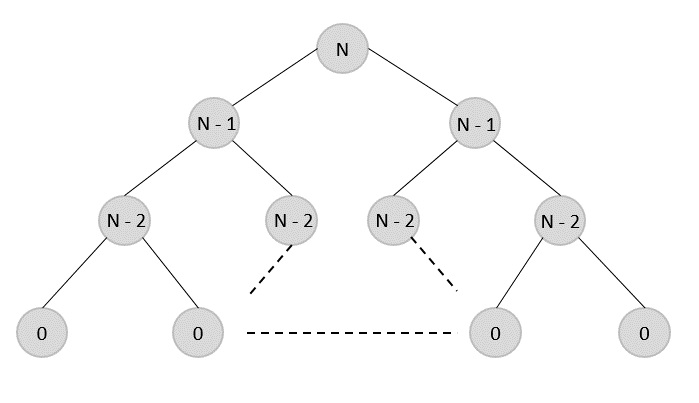
Comparison

In contrast to greedy algorithms, where local optimization is addressed, dynamic algorithms are motivated for an overall optimization of the problem.

In contrast to divide and conquer algorithms, where solutions are combined to achieve an overall solution, dynamic algorithms use the output of a smaller sub-problem and then try to optimize a bigger sub-problem. Dynamic algorithms use Memoization to remember the output of already solved sub-problems.

Example

The following computer problems can be solved using dynamic programming approach −

Fibonacci number series
Knapsack problem
Tower of Hanoi
All pair shortest path by Floyd-Warshall
Shortest path by Dijkstra
Project scheduling

Dynamic programming can be used in both top-down and bottom-up manner. And of course, most of the times, referring to the previous solution output is cheaper than recomputing in terms of CPU cycles.

Data Structures & Algorithm Basic Concepts

This chapter explains the basic terms related to data structure.

Data Definition

Data Definition defines a particular data with the following characteristics.

Atomic − Definition should define a single concept.
Traceable − Definition should be able to be mapped to some data element.
Accurate − Definition should be unambiguous.
Clear and Concise − Definition should be understandable.

Data Object

Data Object represents an object having a data.

Data Type

Data type is a way to classify various types of data such as integer, string, etc. which determines the values that can be used with the corresponding type of data, the type of operations that can be performed on the corresponding type of data. There are two data types −

Built-in Data Type
Derived Data Type

Built-in Data Type

Those data types for which a language has built-in support are known as Built-in Data types. For example, most of the languages provide the following built-in data types.

Integers
Boolean (true, false)
Floating (Decimal numbers)
Character and Strings

Derived Data Type

Those data types which are implementation independent as they can be implemented in one or the other way are known as derived data types. These data types are normally built by the combination of primary or built-in data types and associated operations on them. For example −

List
Array
Stack
Queue

Basic Operations

The data in the data structures are processed by certain operations. The particular data structure chosen largely depends on the frequency of the operation that needs to be performed on the data structure.

Traversing
Searching
Insertion
Deletion
Sorting
Merging

Data Structures and Types

Data structures are introduced in order to store, organize and manipulate data in programming languages. They are designed in a way that makes accessing and processing of the data a little easier and simpler. These data structures are not confined to one particular programming language; they are just pieces of code that structure data in the memory.

Data types are often confused as a type of data structures, but it is not precisely correct even though they are referred to as Abstract Data Types. Data types represent the nature of the data while data structures are just a collection of similar or different data types in one.

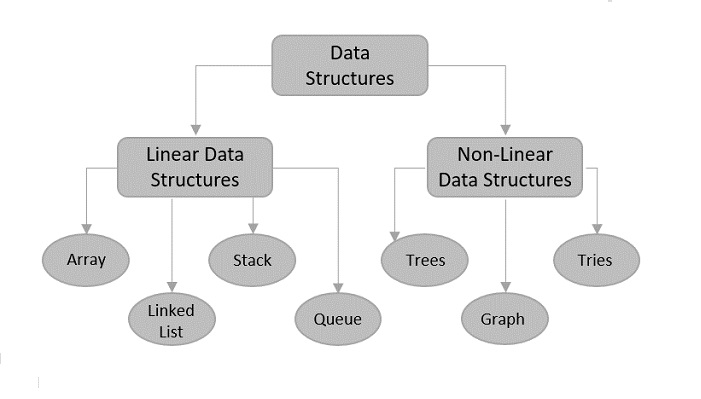
There are usually just two types of data structures −

Linear
Non-Linear

Linear Data Structures

The data is stored in linear data structures sequentially. These are rudimentary structures since the elements are stored one after the other without applying any mathematical operations.

Linear data structures are usually easy to implement but since the memory allocation might become complicated, time and space complexities increase. Few examples of linear data structures include −

Arrays
Linked Lists
Stacks
Queues

Based on the data storage methods, these linear data structures are divided into two sub-types. They are − static and dynamic data structures.

Static Linear Data Structures

In Static Linear Data Structures, the memory allocation is not scalable. Once the entire memory is used, no more space can be retrieved to store more data. Hence, the memory is required to be reserved based on the size of the program. This will also act as a drawback since reserving more memory than required can cause a wastage of memory blocks.

The best example for static linear data structures is an array.

Dynamic Linear Data Structures

In Dynamic linear data structures, the memory allocation can be done dynamically when required. These data structures are efficient considering the space complexity of the program.

Few examples of dynamic linear data structures include: linked lists, stacks and queues.

Non-Linear Data Structures

Non-Linear data structures store the data in the form of a hierarchy. Therefore, in contrast to the linear data structures, the data can be found in multiple levels and are difficult to traverse through.

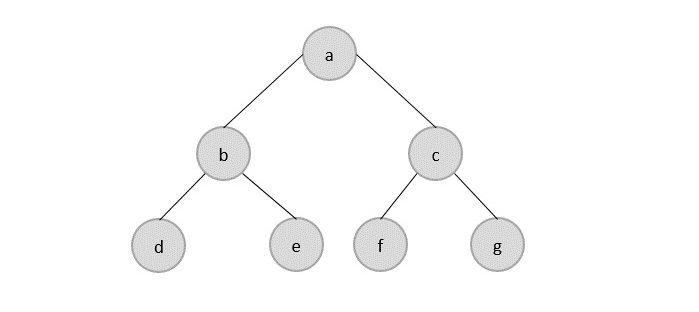
However, they are designed to overcome the issues and limitations of linear data structures. For instance, the main disadvantage of linear data structures is the memory allocation. Since the data is allocated sequentially in linear data structures, each element in these data structures uses one whole memory block. However, if the data uses less memory than the assigned block can hold, the extra memory space in the block is wasted. Therefore, non-linear data structures are introduced. They decrease the space complexity and use the memory optimally.

Few types of non-linear data structures are −

Graphs
Trees
Tries
Maps

Data Structures and Algorithms - Arrays

Array is a type of linear data structure that is defined as a collection of elements with same or different data types. They exist in both single dimension and multiple dimensions. These data structures come into picture when there is a necessity to store multiple elements of similar nature together at one place.

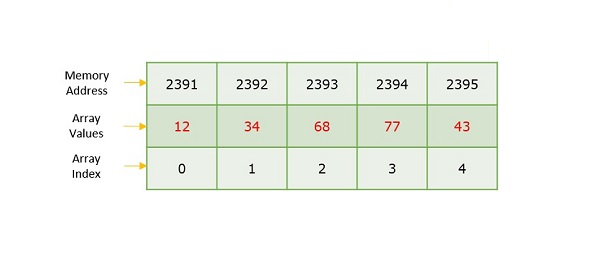
The difference between an array index and a memory address is that the array index acts like a key value to label the elements in the array. However, a memory address is the starting address of free memory available.

Following are the important terms to understand the concept of Array.

Element − Each item stored in an array is called an element.
Index − Each location of an element in an array has a numerical index, which is used to identify the element.

Syntax

Creating an array in C and C++ programming languages −

data_type array_name[array_size] = {elements separated using commas}
or,
data_type array_name[array_size];

Creating an array in JAVA programming language −

data_type[] array_name = {elements separated by commas}
or,
data_type array_name = new data_type[array_size];

Need for Arrays

Arrays are used as solutions to many problems from the small sorting problems to more complex problems like travelling salesperson problem. There are many data structures other than arrays that provide efficient time and space complexity for these problems, so what makes using arrays better? The answer lies in the random access lookup time.

Arrays provide O(1) random access lookup time. That means, accessing the 1^st index of the array and the 1000^th index of the array will both take the same time. This is due to the fact that array comes with a pointer and an offset value. The pointer points to the right location of the memory and the offset value shows how far to look in the said memory.

                           array_name[index]
                              |       |
                           Pointer   Offset

Therefore, in an array with 6 elements, to access the 1st element, array is pointed towards the 0th index. Similarly, to access the 6^th element, array is pointed towards the 5^th index.

Array Representation

Arrays are represented as a collection of buckets where each bucket stores one element. These buckets are indexed from ‘0’ to ‘n-1’, where n is the size of that particular array. For example, an array with size 10 will have buckets indexed from 0 to 9.

This indexing will be similar for the multidimensional arrays as well. If it is a 2-dimensional array, it will have sub-buckets in each bucket. Then it will be indexed as array_name[m][n], where m and n are the sizes of each level in the array.

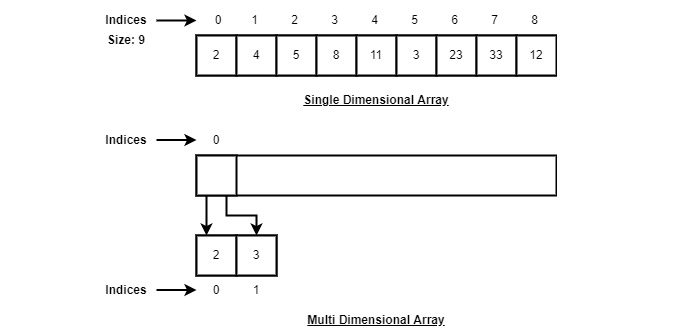
As per the above illustration, following are the important points to be considered.

Index starts with 0.
Array length is 9 which means it can store 9 elements.
Each element can be accessed via its index. For example, we can fetch an element at index 6 as 23.

Basic Operations in the Arrays

The basic operations in the Arrays are insertion, deletion, searching, display, traverse, and update. These operations are usually performed to either modify the data in the array or to report the status of the array.

Following are the basic operations supported by an array.

Traverse − print all the array elements one by one.
Insertion − Adds an element at the given index.
Deletion − Deletes an element at the given index.
Search − Searches an element using the given index or by the value.
Update − Updates an element at the given index.
Display − Displays the contents of the array.

In C, when an array is initialized with size, then it assigns defaults values to its elements in following order.

Data Type	Default Value
bool	false
char	0
int	0
float	0.0
double	0.0f
void
wchar_t	0

Insertion Operation

In the insertion operation, we are adding one or more elements to the array. Based on the requirement, a new element can be added at the beginning, end, or any given index of array. This is done using input statements of the programming languages.

Algorithm

Following is an algorithm to insert elements into a Linear Array until we reach the end of the array −

1. Start
2. Create an Array of a desired datatype and size.
3. Initialize a variable ‘i’ as 0.
4. Enter the element at ith index of the array.
5. Increment i by 1.
6. Repeat Steps 4 & 5 until the end of the array.
7. Stop

Here, we see a practical implementation of insertion operation, where we add data at the end of the array −

Example

C C++ Java

#include <stdio.h>
int main(){
   int LA[3], i;
   printf("Array Before Insertion:\n");
   for(i = 0; i < 3; i++)
      printf("LA[%d] = %d \n", i, LA[i]);
   printf("Inserting Elements.. ");
   printf("The array elements after insertion :\n"); // prints array values
   for(i = 0; i < 3; i++) {
      LA[i] = i + 2;
      printf("LA[%d] = %d \n", i, LA[i]);
   }
   return 0;
}

Output

Array Before Insertion:
LA[0] = 587297216 
LA[1] = 32767 LA[2] = 0 
Inserting Elements.. The array elements after insertion :
LA[0] = 2 
LA[1] = 3 
LA[2] = 4

#include <iostream>
using namespace std;
int main(){
   int LA[3], i;
   cout << "Array Before Insertion:" << endl;
   for(i = 0; i < 3; i++)
      cout << "LA[" << i <<"] = " << LA[i] << endl; 
      
   //prints garbage values
   cout << "Inserting elements.." <<endl;
   cout << "Array After Insertion:" << endl; // prints array values
   for(i = 0; i < 5; i++) {
      LA[i] = i + 2;
      cout << "LA[" << i <<"] = " << LA[i] << endl;
   }
   return 0;
}

Output

Array Before Insertion:
LA[0] = -1834117968
LA[1] = 32767LA[2] = 0
Inserting elements..
Array After Insertion:
LA[0] = 2
LA[1] = 3
LA[2] = 4
LA[5] = 0

public class ArrayDemo {
   public static void main(String []args) {
      int LA[] = new int[3];
      System.out.println("Array Before Insertion:");
      for(int i = 0; i < 3; i++)
         System.out.println("LA[" + i + "] = " + LA[i]); //prints empty array
      System.out.println("Inserting Elements..");
      
      // Printing Array after Insertion
      System.out.println("Array After Insertion:");
      for(int i = 0; i < 3; i++) {
         LA[i] = i+3;
         System.out.println("LA[" + i + "] = " + LA[i]);
      }
   }
}

Output

Array Before Insertion:LA[0] = 0
LA[1] = 0
LA[2] = 0
Inserting Elements..
Array After Insertion:
LA[0] = 3
LA[1] = 4
LA[2] = 5

For other variations of array insertion operation, click here.

Deletion Operation

In this array operation, we delete an element from the particular index of an array. This deletion operation takes place as we assign the value in the consequent index to the current index.

Algorithm

Consider LA is a linear array with N elements and K is a positive integer such that K<=N. Following is the algorithm to delete an element available at the K^th position of LA.

1. Start
2. Set J = K
3. Repeat steps 4 and 5 while J < N
4. Set LA[J] = LA[J + 1]
5. Set J = J+1
6. Set N = N-1
7. Stop

Example

Following are the implementations of this operation in various programming languages −

C C++ Java

#include <stdio.h>
void main(){
   int LA[] = {1,3,5};
   int n = 3;
   int i;
   printf("The original array elements are :\n");
   for(i = 0; i<n; i++)
      printf("LA[%d] = %d \n", i, LA[i]);
   for(i = 1; i<n; i++) {
      LA[i] = LA[i+1];
      n = n – 1;
   }
   printf("The array elements after deletion :\n");
   for(i = 0; i<n-1; i++)
      printf("LA[%d] = %d \n", i, LA[i]);
}

Output

The original array elements are :
LA[0] = 1
LA[1] = 3
LA[2] = 5
The array elements after deletion :
LA[0] = 1
LA[1] = 5

#include <iostream>
using namespace std;
int main(){
   int LA[] = {1,3,5};
   int i, n = 3;
   cout << "The original array elements are :"<<endl;
   for(i = 0; i<n; i++) {
      cout << "LA[" << i << "] = " << LA[i] << endl;
   }
   for(i = 1; i<n; i++) {
      LA[i] = LA[i+1];
      n = n - 1;
   }
   cout << "The array elements after deletion :"<<endl;
   for(i = 0; i<n; i++) {
      cout << "LA[" << i << "] = " << LA[i] <<endl;
   }
}

Output

The original array elements are :
LA[0] = 1
LA[1] = 3
LA[2] = 5
The array elements after deletion :
LA[0] = 1
LA[1] = 5

public class ArrayDemo {
   public static void main(String []args) {
      int LA[] = new int[3];
      int n = LA.length;
      System.out.println("Array Before Deletion:");
      for(int i = 0; i < n; i++) {
         LA[i] = i + 3;
         System.out.println("LA[" + i + "] = " + LA[i]);
      }
      for(int i = 1; i<n-1; i++) {
         LA[i] = LA[i+1];
         n = n - 1;
      }
      System.out.println("Array After Deletion:");
      for(int i = 0; i < n; i++) {
         System.out.println("LA[" + i + "] = " + LA[i]);
      }
   }
}

Output

Array Before Deletion:
LA[0] = 3
LA[1] = 4
LA[2] = 5
Array After Deletion:
LA[0] = 3
LA[1] = 5

Search Operation

Searching an element in the array using a key; The key element sequentially compares every value in the array to check if the key is present in the array or not.

Algorithm

Consider LA is a linear array with N elements and K is a positive integer such that K<=N. Following is the algorithm to find an element with a value of ITEM using sequential search.

1. Start
2. Set J = 0
3. Repeat steps 4 and 5 while J < N
4. IF LA[J] is equal ITEM THEN GOTO STEP 6
5. Set J = J +1
6. PRINT J, ITEM
7. Stop

Example

Following are the implementations of this operation in various programming languages −

C C++ Java

#include <stdio.h>
void main(){
   int LA[] = {1,3,5,7,8};
   int item = 5, n = 5;
   int i = 0, j = 0;
   printf("The original array elements are :\n");
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
   for(i = 0; i<n; i++) {
      if( LA[i] == item ) {
         printf("Found element %d at position %d\n", item, i+1);
      }
   }
}

Output

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
Found element 5 at position 3

#include <iostream>
using namespace std;
int main(){
   int LA[] = {1,3,5,7,8};
   int item = 5, n = 5;
   int i = 0;
   cout << "The original array elements are : " <<endl;
   for(i = 0; i<n; i++) {
      cout << "LA[" << i << "] = " << LA[i] << endl;
   }
   for(i = 0; i<n; i++) {
      if( LA[i] == item ) {
         cout << "Found element " << item << " at position " << i+1 <<endl;
      }
   }
   return 0;
}

Output

The original array elements are : 
LA[0] = 1
LA[1] = 3
LA[2] = 5
LA[3] = 7
LA[4] = 8
Found element 5 at position 3

public class ArrayDemo{
   public static void main(String []args){
      int LA[] = new int[5];
      System.out.println("Array:");
      for(int i = 0; i < 5; i++) {
         LA[i] = i + 3;
         System.out.println("LA[" + i + "] = " + LA[i]);
      }
      for(int i = 0; i < 5; i++) {
         if(LA[i] == 6)
            System.out.println("Element " + 6 + " is found at index " + i);
      }
   }
}

Output

Array:
LA[0] = 3
LA[1] = 4
LA[2] = 5
LA[3] = 6
LA[4] = 7
Element 6 is found at index 3

Traversal Operation

This operation traverses through all the elements of an array. We use loop statements to carry this out.

Algorithm

Following is the algorithm to traverse through all the elements present in a Linear Array −

1 Start
2. Initialize an Array of certain size and datatype.
3. Initialize another variable ‘i’ with 0.
4. Print the ith value in the array and increment i.
5. Repeat Step 4 until the end of the array is reached.
6. End

Example

Following are the implementations of this operation in various programming languages −

C C++ Java

#include <stdio.h>
int main(){
   int LA[] = {1,3,5,7,8};
   int item = 10, k = 3, n = 5;
   int i = 0, j = n;
   printf("The original array elements are :\n");
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Output

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8

#include <iostream>
using namespace std;
int main(){
   int LA[] = {1,3,5,7,8};
   int item = 10, k = 3, n = 5;
   int i = 0, j = n;
   cout << "The original array elements are:\n";
   for(i = 0; i<n; i++)
      cout << "LA[" << i << "] = " << LA[i] << endl;
   return 0;
}

Output

The original array elements are:
LA[0] = 1
LA[1] = 3
LA[2] = 5
LA[3] = 7
LA[4] = 8

public class ArrayDemo {
   public static void main(String []args) {
      int LA[] = new int[5];
      System.out.println("The array elements are: ");
      for(int i = 0; i < 5; i++) {
         LA[i] = i + 2;
         System.out.println("LA[" + i + "] = " + LA[i]);
      }
   }
}

Output

The array elements are: LA[0] = 2
LA[1] = 3
LA[2] = 4
LA[3] = 5
LA[4] = 6

Update Operation

Update operation refers to updating an existing element from the array at a given index.

Algorithm

Consider LA is a linear array with N elements and K is a positive integer such that K<=N. Following is the algorithm to update an element available at the Kth position of LA.

1. Start
2. Set LA[K-1] = ITEM
3. Stop

Example

Following are the implementations of this operation in various programming languages −

C C++ Java

#include <stdio.h>
void main(){
   int LA[] = {1,3,5,7,8};
   int k = 3, n = 5, item = 10;
   int i, j;
   printf("The original array elements are :\n");
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
   LA[k-1] = item;
   printf("The array elements after updation :\n");
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Output

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 LA[3] = 7 
LA[4] = 8 
The array elements after updation :
LA[0] = 1 
LA[1] = 3 
LA[2] = 10 
LA[3] = 7 
LA[4] = 8

#include <iostream>
using namespace std;
int main(){
   int LA[] = {1,3,5,7,8};
   int item = 10, k = 3, n = 5;
   int i = 0, j = n;
   cout << "The original array elements are :\n";
   for(i = 0; i<n; i++)
      cout << "LA[" << i << "] = " << LA[i] << endl;
   LA[2] = item;
   cout << "The array elements after updation are :\n";
   for(i = 0; i<n; i++)
      cout << "LA[" << i << "] = " << LA[i] << endl;
   return 0;
}

Output

The original array elements are :
LA[0] = 1
LA[1] = 3
LA[2] = 5
LA[3] = 7
LA[4] = 8
The array elements after updation are :
LA[0] = 1
LA[1] = 3
LA[2] = 10
LA[3] = 7
LA[4] = 8

public class ArrayDemo {
   public static void main(String []args) {
      int LA[] = new int[5];
      int item = 15;
      System.out.println("The array elements are: ");
      for(int i = 0; i < 5; i++) {
         LA[i] = i + 2;
         System.out.println("LA[" + i + "] = " + LA[i]);
      }
      LA[3] = item;
      System.out.println("The array elements after updation are: ");
      for(int i = 0; i < 5; i++)
         System.out.println("LA[" + i + "] = " + LA[i]);
   }
}

Output

The array elements are: 
LA[0] = 2
LA[1] = 3
LA[2] = 4
LA[3] = 5
LA[4] = 6
The array elements after updation are: 
LA[0] = 2
LA[1] = 3
LA[2] = 4
LA[3] = 15
LA[4] = 6

Display Operation

This operation displays all the elements in the entire array using a print statement.

Algorithm

1. Start
2. Print all the elements in the Array
3. Stop

Example

Following are the implementations of this operation in various programming languages −

C C++ Java

#include <stdio.h>
int main(){
   int LA[] = {1,3,5,7,8};
   int n = 5;
   int i;
   printf("The original array elements are :\n");
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Output

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8

#include <iostream>
using namespace std;
int main(){
   int LA[] = {1,3,5,7,8};
   int n = 5;
   int i;
   cout << "The original array elements are :\n";
   for(i = 0; i<n; i++)
      cout << "LA[" << i << "] = " << LA[i] << endl;
   return 0;
}

Output

The original array elements are :
LA[0] = 1
LA[1] = 3
LA[2] = 5
LA[3] = 7
LA[4] = 8

public class ArrayDemo {
   public static void main(String []args) {
      int LA[] = new int[5];
      System.out.println("The array elements are: ");
      for(int i = 0; i < 5; i++) {
         LA[i] = i + 2;
         System.out.println("LA[" + i + "] = " + LA[i]);
      }
   }
}

Output

The array elements are: 
LA[0] = 2
LA[1] = 3
LA[2] = 4
LA[3] = 5
LA[4] = 6

Data Structure and Algorithms - Linked List

If arrays accommodate similar types of data types, linked lists consist of elements with different data types that are also arranged sequentially.

But how are these linked lists created?

A linked list is a collection of “nodes” connected together via links. These nodes consist of the data to be stored and a pointer to the address of the next node within the linked list. In the case of arrays, the size is limited to the definition, but in linked lists, there is no defined size. Any amount of data can be stored in it and can be deleted from it.

There are three types of linked lists −

Singly Linked List − The nodes only point to the address of the next node in the list.
Doubly Linked List − The nodes point to the addresses of both previous and next nodes.
Circular Linked List − The last node in the list will point to the first node in the list. It can either be singly linked or doubly linked.

Linked List Representation

Linked list can be visualized as a chain of nodes, where every node points to the next node.

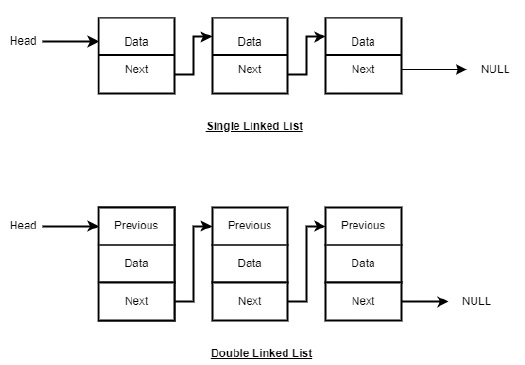
As per the above illustration, following are the important points to be considered.

Linked List contains a link element called first (head).
Each link carries a data field(s) and a link field called next.
Each link is linked with its next link using its next link.
Last link carries a link as null to mark the end of the list.

Types of Linked List

Following are the various types of linked list.

Singly Linked Lists

Singly linked lists contain two “buckets” in one node; one bucket holds the data and the other bucket holds the address of the next node of the list. Traversals can be done in one direction only as there is only a single link between two nodes of the same list.

Doubly Linked Lists

Doubly Linked Lists contain three “buckets” in one node; one bucket holds the data and the other buckets hold the addresses of the previous and next nodes in the list. The list is traversed twice as the nodes in the list are connected to each other from both sides.

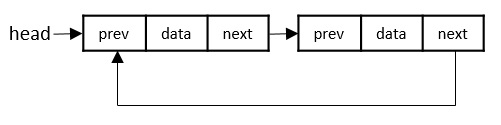
Circular Linked Lists

Circular linked lists can exist in both singly linked list and doubly linked list.

Since the last node and the first node of the circular linked list are connected, the traversal in this linked list will go on forever until it is broken.

Basic Operations in the Linked Lists

The basic operations in the linked lists are insertion, deletion, searching, display, and deleting an element at a given key. These operations are performed on Singly Linked Lists as given below −

Insertion − Adds an element at the beginning of the list.
Deletion − Deletes an element at the beginning of the list.
Display − Displays the complete list.
Search − Searches an element using the given key.
Delete − Deletes an element using the given key.

Insertion Operation

Adding a new node in linked list is a more than one step activity. We shall learn this with diagrams here. First, create a node using the same structure and find the location where it has to be inserted.

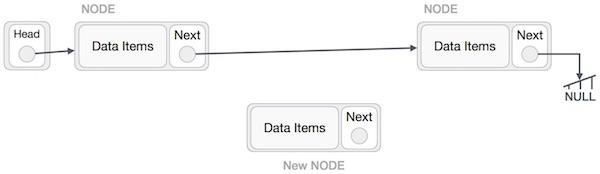
Imagine that we are inserting a node B (NewNode), between A (LeftNode) and C (RightNode). Then point B.next to C −

NewNode.next −> RightNode;

It should look like this −

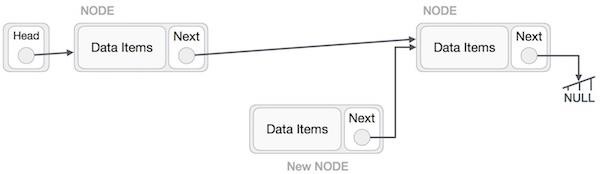
Now, the next node at the left should point to the new node.

LeftNode.next −> NewNode;

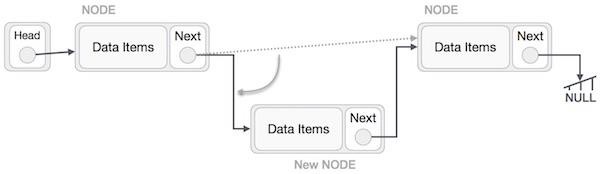
This will put the new node in the middle of the two. The new list should look like this −

Insertion in linked list can be done in three different ways. They are explained as follows −

Insertion at Beginning

In this operation, we are adding an element at the beginning of the list.

Algorithm

1. START
2. Create a node to store the data
3. Check if the list is empty
4. If the list is empty, add the data to the node and assign the head pointer to it.
5 If the list is not empty, add the data to a node and link to the current head. Assign the head to the newly added node.
6. END

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;

// display the list
void printList(){
   struct node *p = head;
   printf("\n[");
   
   //start from the beginning
   while(p != NULL) {
      printf(" %d ",p->data);
      p = p->next;
   }
   printf("]");
}

//insertion at the beginning
void insertatbegin(int data){
   
   //create a link
   struct node *lk = (struct node*) malloc(sizeof(struct node));
   lk->data = data;
   
   // point it to old first node
   lk->next = head;
   
   //point first to new first node
   head = lk;
}
void main(){
   int k=0;
   insertatbegin(12);
   insertatbegin(22);
   insertatbegin(30);
   insertatbegin(44);
   insertatbegin(50);
   printf("Linked List: ");
   
   // print list
   printList();
}

Output

Linked List: 
[ 50  44  30  22  12 ]

#include <bits/stdc++.h>
#include <string>
using namespace std;
struct node {
   int data;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;

// display the list
void printList(){
   struct node *p = head;
   cout << "\n[";
   
   //start from the beginning
   while(p != NULL) {
      cout << " " << p->data << " ";
      p = p->next;
   }
   cout << "]";
}

//insertion at the beginning
void insertatbegin(int data){
   
   //create a link
   struct node *lk = (struct node*) malloc(sizeof(struct node));
   lk->data = data;
   
   // point it to old first node
   lk->next = head;
   
   //point first to new first node
   head = lk;
}
int main(){
   insertatbegin(12);
   insertatbegin(22);
   insertatbegin(30);
   insertatbegin(44);
   insertatbegin(50);
   cout << "Linked List: ";
   
   // print list
   printList();
}

Output

Linked List: 
[ 50  44  30  22  12 ]

public class Linked_List {
   static class node {
      int data;
      node next;
      node (int value) {
         data = value;
         next = null;
      }
   }
   static node head;
   
   // display the list
   static void printList() {
      node p = head;
      System.out.print("\n[");
   
      //start from the beginning
      while(p != null) {
         System.out.print(" " + p.data + " ");
         p = p.next;
      }
      System.out.print("]");
   }

   //insertion at the beginning
   static void insertatbegin(int data) {

      //create a link
      node lk = new node(data);;

      // point it to old first node
      lk.next = head;

      //point first to new first node
      head = lk;
   }
   public static void main(String args[]) {
      int k=0;
      insertatbegin(12);
      insertatbegin(22);
      insertatbegin(30);
      insertatbegin(44);
      insertatbegin(50);
      insertatbegin(33);
      System.out.println("Linked List: ");
      
      // print list
      printList();
   }
}

Output

Linked List: 

[33  50  44  30  22  12 ]

class Node:
   def __init__(self, data=None):
      self.data = data
      self.next = None
class SLL:
   def __init__(self):
      self.head = None

# Print the linked list
   def listprint(self):
      printval = self.head
      print("Linked List: ")
      while printval is not None:
         print (printval.data)
         printval = printval.next
   def AddAtBeginning(self,newdata):
      NewNode = Node(newdata)

      # Update the new nodes next val to existing node
      NewNode.next = self.head
      self.head = NewNode

l1 = SLL()
l1.head = Node("731")
e2 = Node("672")
e3 = Node("63")

l1.head.next = e2
e2.next = e3

l1.AddAtBeginning("122")
l1.listprint()

Output

Linked List: 
122
731
672
63

Insertion at Ending

In this operation, we are adding an element at the ending of the list.

Algorithm

1. START
2. Create a new node and assign the data
3. Find the last node
4. Point the last node to new node
5. END

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;

// display the list
void printList(){
   struct node *p = head;
   printf("\n[");
   
   //start from the beginning
   while(p != NULL) {
      printf(" %d ",p->data);
      p = p->next;
   }
   printf("]");
}

//insertion at the beginning
void insertatbegin(int data){

   //create a link
   struct node *lk = (struct node*) malloc(sizeof(struct node));
   lk->data = data;

   // point it to old first node
   lk->next = head;
   
   //point first to new first node
   head = lk;
}
void insertatend(int data){

   //create a link
   struct node *lk = (struct node*) malloc(sizeof(struct node));
   lk->data = data;
   struct node *linkedlist = head;

   // point it to old first node
   while(linkedlist->next != NULL)
      linkedlist = linkedlist->next;

   //point first to new first node
   linkedlist->next = lk;
}
void main(){
   int k=0;
   insertatbegin(12);
   insertatend(22);
   insertatend(30);
   insertatend(44);
   insertatend(50);
   printf("Linked List: ");
   
   // print list
   printList();
}

Output

Linked List:
[ 12 22 30 44 50 ]

#include <bits/stdc++.h>
#include <string>
using namespace std;
struct node {
   int data;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;

// display the list
void printList(){
   struct node *p = head;
   cout << "\n[";
   
   //start from the beginning
   while(p != NULL) {
      cout << " " << p->data << " ";
      p = p->next;
   }
   cout << "]";
}

//insertion at the beginning
void insertatbegin(int data){

   //create a link
   struct node *lk = (struct node*) malloc(sizeof(struct node));
   lk->data = data;

   // point it to old first node
   lk->next = head;

   //point first to new first node
   head = lk;
}
void insertatend(int data){
   
   //create a link
   struct node *lk = (struct node*) malloc(sizeof(struct node));
   lk->data = data;
   struct node *linkedlist = head;

   // point it to old first node
   while(linkedlist->next != NULL)
      linkedlist = linkedlist->next;

   //point first to new first node
   linkedlist->next = lk;
}
int main(){
   insertatbegin(12);
   insertatend(22);
   insertatbegin(30);
   insertatend(44);
   insertatbegin(50);
   cout << "Linked List: ";

   // print list
   printList();
}

Output

Linked List: 
[ 50  30  12  22  44 ]

public class Linked_List {
   static class node {
      int data;
      node next;
      node (int value) {
         data = value;
         next = null;
      }
   }
   static node head;

   // display the list
   static void printList() {
      node p = head;
      System.out.print("\n[");

      //start from the beginning
      while(p != null) {
         System.out.print(" " + p.data + " ");
         p = p.next;
      }
      System.out.print("]");
   }

   //insertion at the beginning
   static void insertatbegin(int data) {

      //create a link
      node lk = new node(data);;

      // point it to old first node
      lk.next = head;

      //point first to new first node
      head = lk;
   }
   static void insertatend(int data) {
   
      //create a link
      node lk = new node(data);
      node linkedlist = head;

      // point it to old first node
      while(linkedlist.next != null)
         linkedlist = linkedlist.next;

      //point first to new first node
      linkedlist.next = lk;
   }
   public static void main(String args[]) {
      int k=0;
      insertatbegin(12);
      insertatbegin(22);
      insertatbegin(30);
      insertatend(44);
      insertatend(50);
      insertatend(33);
      System.out.println("Linked List: ");

      // print list
      printList();
   }
}

Output

Linked List: 
[ 30  22  12  44 50  33 ]

class Node:
   def __init__(self, data=None):
      self.data = data
      self.next = None
class LL:
   def __init__(self):
      self.head = None
   def listprint(self):
      val = self.head
      print("Linked List:")
      while val is not None:
         print(val.data)
         val = val.next

l1 = LL()
l1.head = Node("23")
l2 = Node("12")
l3 = Node("7")
l4 = Node("14")
l5 = Node("61")

# Linking the first Node to second node
l1.head.next = l2

# Linking the second Node to third node
l2.next = l3
l3.next = l4
l4.next = l5
l1.listprint()

Output

Linked List:
23
12
7
14
61

Insertion at a Given Position

In this operation, we are adding an element at any position within the list.

Algorithm

1. START
2. Create a new node and assign data to it
3. Iterate until the node at position is found
4. Point first to new first node
5. END

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;

// display the list
void printList(){
   struct node *p = head;
   printf("\n[");
   
   //start from the beginning
   while(p != NULL) {
      printf(" %d ",p->data);
      p = p->next;
   }
   printf("]");
}

//insertion at the beginning
void insertatbegin(int data){

   //create a link
   struct node *lk = (struct node*) malloc(sizeof(struct node));
   lk->data = data;

   // point it to old first node
   lk->next = head;

   //point first to new first node
   head = lk;
}
void insertafternode(struct node *list, int data){
   struct node *lk = (struct node*) malloc(sizeof(struct node));
   lk->data = data;
   lk->next = list->next;
   list->next = lk;
}
void main(){
   int k=0;
   insertatbegin(12);
   insertatbegin(22);
   insertafternode(head->next, 30);
   printf("Linked List: ");

   // print list
   printList();
}

Output

Linked List:
[ 22 12 30 ]

#include <bits/stdc++.h>
#include <string>
using namespace std;
struct node {
   int data;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;

// display the list
void printList(){
   struct node *p = head;
   cout << "\n[";
   
   //start from the beginning
   while(p != NULL) {
      cout << " " << p->data << " ";
      p = p->next;
   }
   cout << "]";
}

//insertion at the beginning
void insertatbegin(int data){

   //create a link
   struct node *lk = (struct node*) malloc(sizeof(struct node));
   lk->data = data;

   // point it to old first node
   lk->next = head;

   //point first to new first node
   head = lk;
}
void insertafternode(struct node *list, int data){
   struct node *lk = (struct node*) malloc(sizeof(struct node));
   lk->data = data;
   lk->next = list->next;
   list->next = lk;
}
int main(){
   insertatbegin(12);
   insertatbegin(22);
   insertatbegin(30);
   insertafternode(head->next,44);
   insertafternode(head->next->next, 50);
   cout << "Linked List: ";

   // print list
   printList();
}

Output

Linked List: 
[ 30  22  44  50  12 ]

public class Linked_List {
   static class node {
      int data;
      node next;
      node (int value) {
         data = value;
         next = null;
      }
   }
   static node head;

   // display the list
   static void printList() {
      node p = head;
      System.out.print("\n[");

      //start from the beginning
      while(p != null) {
         System.out.print(" " + p.data + " ");
         p = p.next;
      }
      System.out.print("]");
   }

   //insertion at the beginning
   static void insertatbegin(int data) {

      //create a link
      node lk = new node(data);;

      // point it to old first node
      lk.next = head;

      //point first to new first node
      head = lk;
   }
   static void insertafternode(node list, int data) {
      node lk = new node(data);
      lk.next = list.next;
      list.next = lk;
   }
   public static void main(String args[]) {
      int k=0;
      insertatbegin(12);
      insertatbegin(22);
      insertatbegin(30);
      insertatbegin(44);
      insertafternode(head.next, 50);
      insertafternode(head.next.next, 33);
      System.out.println("Linked List: ");

      // print list
      printList();
   }
}

Output

Linked List: 

[44  30  50  33  22  12 ]

class Node:
   def __init__(self, data=None):
      self.data = data
      self.next = None

class SLL:
   def __init__(self):
      self.head = None

# Print the linked list
   def listprint(self):
      printval = self.head
      print("Linked List: ")
      while printval is not None:
         print (printval.data)
         printval = printval.next

   # Function to add node
   def InsertAtPos(self,nodeatpos,newdata):
      if nodeatpos is None:
         print("The mentioned node is absent")
         return
      NewNode = Node(newdata)
      NewNode.next = nodeatpos.next
      nodeatpos.next = NewNode

l1 = SLL()
l1.head = Node("731")
e2 = Node("672")
e3 = Node("63")

l1.head.next = e2
e2.next = e3

l1.InsertAtPos(l1.head.next, "122")
l1.listprint()

Output

Linked List: 
731
672
122
63

Deletion Operation

Deletion is also a more than one step process. We shall learn with pictorial representation. First, locate the target node to be removed, by using searching algorithms.

The left (previous) node of the target node now should point to the next node of the target node −

LeftNode.next −> TargetNode.next;

This will remove the link that was pointing to the target node. Now, using the following code, we will remove what the target node is pointing at.

TargetNode.next −> NULL;

We need to use the deleted node. We can keep that in memory otherwise we can simply deallocate memory and wipe off the target node completely.

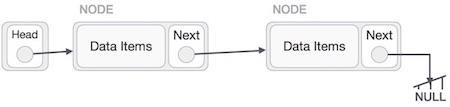
Similar steps should be taken if the node is being inserted at the beginning of the list. While inserting it at the end, the second last node of the list should point to the new node and the new node will point to NULL.

Deletion in linked lists is also performed in three different ways. They are as follows −

Deletion at Beginning

In this deletion operation of the linked, we are deleting an element from the beginning of the list. For this, we point the head to the second node.

Algorithm

1. START
2. Assign the head pointer to the next node in the list
3. END

Example

Following are the implementations of this operation in various programming languages −

C C++ Java

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;

// display the list
void printList(){
   struct node *p = head;
   printf("\n[");
   
   //start from the beginning
   while(p != NULL) {
      printf(" %d ",p->data);
      p = p->next;
   }
   printf("]");
}

//insertion at the beginning
void insertatbegin(int data){

   //create a link
   struct node *lk = (struct node*) malloc(sizeof(struct node));
   lk->data = data;

   // point it to old first node
   lk->next = head;

   //point first to new first node
   head = lk;
}
void deleteatbegin(){
   head = head->next;
}
void main(){
   int k=0;
   insertatbegin(12);
   insertatbegin(22);
   insertatbegin(30);
   insertatbegin(40);
   insertatbegin(55);
   printf("Linked List: ");
   
   // print list
   printList();
   deleteatbegin();
   printf("\nLinked List after deletion: ");
   
   // print list
   printList();
}

Output

Linked List: 
[ 55  40  30  22  12 ]
Linked List after deletion: 
[ 40  30  22  12 ]

#include <bits/stdc++.h>
#include <string>
using namespace std;
struct node {
   int data;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;

// display the list
void printList(){
   struct node *p = head;
   cout << "\n[";
   
   //start from the beginning
   while(p != NULL) {
      cout << " " << p->data << " ";
      p = p->next;
   }
   cout << "]";
}

//insertion at the beginning
void insertatbegin(int data){
   
   //create a link
   struct node *lk = (struct node*) malloc(sizeof(struct node));
   lk->data = data;

   // point it to old first node
   lk->next = head;

   //point first to new first node
   head = lk;
}
void deleteatbegin(){
   head = head->next;
}
int main(){
   insertatbegin(12);
   insertatbegin(22);
   insertatbegin(30);
   insertatbegin(44);
   insertatbegin(50);
   cout << "Linked List: ";

   // print list
   printList();
   deleteatbegin();
   cout << "Linked List after deletion: ";
   printList();
}

Output

Linked List: 
[ 50  44  30  22  12 ]
Linked List after deletion: 
[ 44  30  22  12 ]

 
public class Linked_List {
   static class node {
      int data;
      node next;
      node (int value) {
         data = value;
         next = null;
      }
   }
   static node head;
   
   // display the list
   static void printList() {
      node p = head;
      System.out.print("\n[");
      
      //start from the beginning
      while(p != null) {
         System.out.print(" " + p.data + " ");
         p = p.next;
      }
      System.out.print("]");
   }
   
   //insertion at the beginning
   static void insertatbegin(int data) {

      //create a link
      node lk = new node(data);;
      
      // point it to old first node
      lk.next = head;
      
      //point first to new first node
      head = lk;
   }
   static void deleteatbegin() {
      head = head.next;
   }
   public static void main(String args[]) {
      int k=0;
      insertatbegin(12);
      insertatbegin(22);
      insertatbegin(30);
      insertatbegin(44);
      insertatbegin(50);
      insertatbegin(33);
      System.out.println("Linked List: ");
      
      // print list
      printList();
      deleteatbegin();
      System.out.println("\nLinked List after deletion: ");
      
      // print list
      printList();
   }
}

Output

Linked List: 
[ 33  50  44  30  22  12 ]
Linked List after deletion: 

[50  44  30  22  12 ]

Deletion at Ending

In this deletion operation of the linked, we are deleting an element from the ending of the list.

Algorithm

1. START
2. Iterate until you find the second last element in the list.
3. Assign NULL to the second last element in the list.
4. END

Example

Following are the implementations of this operation in various programming languages −

C C++ Java

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;

// display the list
void printList(){
   struct node *p = head;
   printf("\n[");
   
   //start from the beginning
   while(p != NULL) {
      printf(" %d ",p->data);
      p = p->next;
   }
   printf("]");
}

//insertion at the beginning
void insertatbegin(int data){
   
   //create a link
   struct node *lk = (struct node*) malloc(sizeof(struct node));
   lk->data = data;

   // point it to old first node
   lk->next = head;

   //point first to new first node
   head = lk;
}
void deleteatend(){
   struct node *linkedlist = head;
   while (linkedlist->next->next != NULL)
      linkedlist = linkedlist->next;
   linkedlist->next = NULL;
}
void main(){
   int k=0;
   insertatbegin(12);
   insertatbegin(22);
   insertatbegin(30);
   insertatbegin(40);
   insertatbegin(55);
   printf("Linked List: ");
   
   // print list
   printList();
   deleteatend();
   printf("\nLinked List after deletion: ");
   
   // print list
   printList();
}

Output

Linked List: 
[ 55  40  30  22  12 ]
Linked List after deletion: 
[ 55  40  30  22 ]

#include <bits/stdc++.h>
#include <string>
using namespace std;
struct node {
   int data;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;

// Displaying the list
void printList(){
   struct node *p = head;
   while(p != NULL) {
      cout << " " << p->data << " ";
      p = p->next;
   }
}

// Insertion at the beginning
void insertatbegin(int data){
   
   //create a link
   struct node *lk = (struct node*) malloc(sizeof(struct node));
   lk->data = data;
   
   // point it to old first node
   lk->next = head;

   //point first to new first node
   head = lk;
}
void deleteatend(){
   struct node *linkedlist = head;
   while (linkedlist->next->next != NULL)
      linkedlist = linkedlist->next;
   linkedlist->next = NULL;
}
int main(){
   insertatbegin(12);
   insertatbegin(22);
   insertatbegin(30);
   insertatbegin(44);
   insertatbegin(50);
   cout << "Linked List: ";

   // print list
   printList();
   deleteatend();
   cout << "\nLinked List after deletion: ";
   printList();
}

Output

Linked List:  50  44  30  22  12 
Linked List after deletion:  50  44  30  22

public class Linked_List {
   static class node {
      int data;
      node next;
      node (int value) {
         data = value;
         next = null;
      }
   }
   static node head;
   
   // display the list
   static void printList() {
      node p = head;
      System.out.print("\n[");
      
      //start from the beginning
      while(p != null) {
         System.out.print(" " + p.data + " ");
         p = p.next;
      }
      System.out.print("]");
   }
   
   //insertion at the beginning
   static void insertatbegin(int data) {
      
      //create a link
      node lk = new node(data);;
      
      // point it to old first node
      lk.next = head;

      //point first to new first node
      head = lk;
   }
   static void deleteatend() {
      node linkedlist = head;
      while (linkedlist.next.next != null)
         linkedlist = linkedlist.next;
      linkedlist.next = null;
   }
   public static void main(String args[]) {
      int k=0;
      insertatbegin(12);
      insertatbegin(22);
      insertatbegin(30);
      insertatbegin(44);
      insertatbegin(50);
      insertatbegin(33);
      System.out.println("Linked List: ");

      // print list
      printList();

      //deleteatbegin();
      deleteatend();
      System.out.println("\nLinked List after deletion: ");

      // print list
      printList();
   }
}

Output

Linked List: 
[ 33  50  44  30  22  12 ]
Linked List after deletion: 

[ 33  50  44  30  22 ]

Deletion at a Given Position

In this deletion operation of the linked, we are deleting an element at any position of the list.

Algorithm

1. START
2. Iterate until find the current node at position in the list
3. Assign the adjacent node of current node in the list to its previous node.
4. END

Example

Following are the implementations of this operation in various programming languages −

C C++ Java

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;

// display the list
void printList(){
   struct node *p = head;
   printf("\n[");

   //start from the beginning
   while(p != NULL) {
      printf(" %d ",p->data);
      p = p->next;
   }
   printf("]");
}

//insertion at the beginning
void insertatbegin(int data){

   //create a link
   struct node *lk = (struct node*) malloc(sizeof(struct node));
   lk->data = data;

   // point it to old first node
   lk->next = head;

   //point first to new first node
   head = lk;
}
void deletenode(int key){
   struct node *temp = head, *prev;
   if (temp != NULL && temp->data == key) {
      head = temp->next;
      return;
   }

   // Find the key to be deleted
   while (temp != NULL && temp->data != key) {
      prev = temp;
      temp = temp->next;
   }

   // If the key is not present
   if (temp == NULL) return;

   // Remove the node
   prev->next = temp->next;
}
void main(){
   int k=0;
   insertatbegin(12);
   insertatbegin(22);
   insertatbegin(30);
   insertatbegin(40);
   insertatbegin(55);
   printf("Linked List: ");

   // print list
   printList();
   deletenode(30);
   printf("\nLinked List after deletion: ");

   // print list
   printList();
}

Output

Linked List: 
[ 55  40  30  22  12 ]
Linked List after deletion: 
[ 55  40  22  12 ]

#include <bits/stdc++.h>
#include <string>
using namespace std;
struct node {
   int data;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;

// display the list
void printList(){
   struct node *p = head;
   cout << "\n[";

   //start from the beginning
   while(p != NULL) {
      cout << " " << p->data << " ";
      p = p->next;
   }
   cout << "]";
}

//insertion at the beginning
void insertatbegin(int data){

   //create a link
   struct node *lk = (struct node*) malloc(sizeof(struct node));
   lk->data = data;

   // point it to old first node
   lk->next = head;

   //point first to new first node
   head = lk;
}
void deletenode(int key){
   struct node *temp = head, *prev;
   if (temp != NULL && temp->data == key) {
      head = temp->next;
      return;
   }

   // Find the key to be deleted
   while (temp != NULL && temp->data != key) {
      prev = temp;
      temp = temp->next;
   }

   // If the key is not present
   if (temp == NULL) return;

   // Remove the node
   prev->next = temp->next;
}
int main(){
   insertatbegin(12);
   insertatbegin(22);
   insertatbegin(30);
   insertatbegin(44);
   insertatbegin(50);
   cout << "Linked List: ";

   // print list
   printList();
   deletenode(30);
   cout << "Linked List after deletion: ";
   printList();
}

Output

Linked List: 
[ 50  44  30  22  12 ]Linked List after deletion: 
[ 50  44  22  12 ]

public class Linked_List {
   static class node {
      int data;
      node next;
      node (int value) {
         data = value;
         next = null;
      }
   }
   static node head;
   
   // display the list
   static void printList() {
      node p = head;
      System.out.print("\n[");
   
      //start from the beginning
      while(p != null) {
         System.out.print(" " + p.data + " ");
         p = p.next;
      }
      System.out.print("]");
   }
   
   //insertion at the beginning
   static void insertatbegin(int data) {

   
      //create a link
      node lk = new node(data);;

      // point it to old first node
      lk.next = head;

      //point first to new first node
      head = lk;
   }
   static void deletenode(int key) {
      node temp = head;
      node prev = null;
      if (temp != null && temp.data == key) {
         head = temp.next;
         return;
      }
      
      // Find the key to be deleted
      while (temp != null && temp.data != key) {
         prev = temp;
         temp = temp.next;
      }
      
      // If the key is not present
      if (temp == null) return;
      
      // Remove the node
      prev.next = temp.next;
   }
   public static void main(String args[]) {
      int k=0;
      insertatbegin(12);
      insertatbegin(22);
      insertatbegin(30);
      insertatbegin(44);
      insertatbegin(50);
      insertatbegin(33);
      System.out.println("Linked List: ");

      // print list
      printList();

      //deleteatbegin();
      //deleteatend();
      deletenode(12);
      System.out.println("\nLinked List after deletion: ");

      // print list
      printList();
   }
}

Output

Linked List: 

[ 33  50  44  30  22  12 ]
Linked List after deletion: 

[ 33  50  44  30  22 ]

Reverse Operation

This operation is a thorough one. We need to make the last node to be pointed by the head node and reverse the whole linked list.

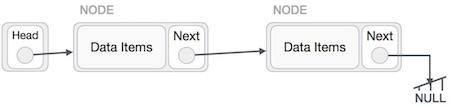
First, we traverse to the end of the list. It should be pointing to NULL. Now, we shall make it point to its previous node −

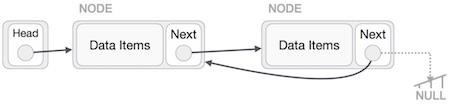
We have to make sure that the last node is not the last node. So we'll have some temp node, which looks like the head node pointing to the last node. Now, we shall make all left side nodes point to their previous nodes one by one.

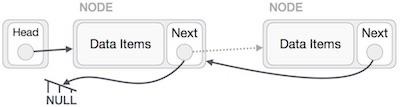
Except the node (first node) pointed by the head node, all nodes should point to their predecessor, making them their new successor. The first node will point to NULL.

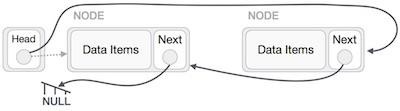
We'll make the head node point to the new first node by using the temp node.

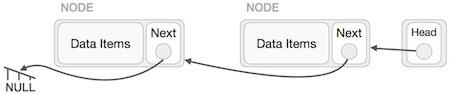
Algorithm

Step by step process to reverse a linked list is as follows −

1 START
2. We use three pointers to perform the reversing: prev, next, head.
3. Point the current node to head and assign its next value to the prev node.
4. Iteratively repeat the step 3 for all the nodes in the list.
5. Assign head to the prev node.

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;

// display the list
void printList(){
   struct node *p = head;
   printf("\n[");
   
   //start from the beginning
   while(p != NULL) {
      printf(" %d ",p->data);
      p = p->next;
   }
   printf("]");
}

//insertion at the beginning
void insertatbegin(int data){

   //create a link
   struct node *lk = (struct node*) malloc(sizeof(struct node));
   lk->data = data;

   // point it to old first node
   lk->next = head;

   //point first to new first node
   head = lk;
}
void reverseList(struct node** head){
   struct node *prev = NULL, *cur=*head, *tmp;
   while(cur!= NULL) {
      tmp = cur->next;
      cur->next = prev;
      prev = cur;
      cur = tmp;
   }
   *head = prev;
}
void main(){
   int k=0;
   insertatbegin(12);
   insertatbegin(22);
   insertatbegin(30);
   insertatbegin(40);
   insertatbegin(55);
   printf("Linked List: ");

   // print list
   printList();
   reverseList(&head);
   printf("\nReversed Linked List: ");
   printList();
}

Output

Linked List: 
[ 55  40  30  22  12 ]
Reversed Linked List: 
[ 12  22  30  40  55 ]

#include <bits/stdc++.h>
struct node {
   int data;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;

// display the list
void printList(){
   struct node *p = head;
   printf("\n[");

   //start from the beginning
   while(p != NULL) {
      printf(" %d ",p->data);
      p = p->next;
   }
   printf("]");
}

//insertion at the beginning
void insertatbegin(int data){

   //create a link
   struct node *lk = (struct node*) malloc(sizeof(struct node));
   lk->data = data;

   // point it to old first node
   lk->next = head;

   //point first to new first node
   head = lk;
}
void reverseList(struct node** head){
   struct node *prev = NULL, *cur=*head, *tmp;
   while(cur!= NULL) {
      tmp = cur->next;
      cur->next = prev;
      prev = cur;
      cur = tmp;
   }
   *head = prev;
}
int main(){
   int k=0;
   insertatbegin(12);
   insertatbegin(22);
   insertatbegin(30);
   insertatbegin(40);
   insertatbegin(55);
   printf("Linked List: ");

   // print list
   printList();
   reverseList(&head);
   printf("\nReversed Linked List: ");
   printList();
   return 0;
}

Output

Linked List: 
[ 55  40  30  22  12 ]
Reversed Linked List: 
[ 12  22  30  40  55 ]

public class Linked_List {
   static Node head;
   static class Node {
      int data;
      Node next;
      Node (int value) {
         data = value;
         next = null;
      }
   }

   // display the list
   static void printList(Node node) {
      System.out.print("\n[");

      //start from the beginning
      while(node != null) {
         System.out.print(" " + node.data + " ");
         node = node.next;
      }
      System.out.print("]");
   }
   static Node reverseList(Node head) {
      Node prev = null;
      Node cur = head;
      Node temp = null;
      while (cur != null) {
         temp = cur.next;
         cur.next = prev;
         prev = cur;
         cur = temp;
      }
      head = prev;
      return head;
   }
   public static void main(String args[]) {
      Linked_List list = new Linked_List();
      list.head = new Node(33);
      list.head.next = new Node(50);
      list.head.next.next = new Node(44);
      list.head.next.next.next = new Node(22);
      list.head.next.next.next.next = new Node(12);
      System.out.println("Linked List: ");
      
      // print list
      list.printList(head);
      head = list.reverseList(head);
      System.out.println("\nReversed linked list ");
      list.printList(head);
   }
}

Output

Linked List: 
[ 33  50  44  22  12 ]
Reversed linked list 

[ 12 22  44  50  33 ]

class Node:
   def __init__(self, data=None):
      self.data = data
      self.next = None

class SLL:
   def __init__(self):
      self.head = None

# Print the linked list
   def listprint(self):
      printval = self.head
      print("Linked List: ")
      while printval is not None:
         print (printval.data)
         printval = printval.next
   def reverse(self):
      prev = None
      curr = self.head
      while(curr is not None):
         next = curr.next
         curr.next = prev
         prev = curr
         curr = next
      self.head = prev

l1 = SLL()
l1.head = Node("731")
e2 = Node("672")
e3 = Node("63")

l1.head.next = e2
e2.next = e3

l1.listprint()
l1.reverse()
print("After reversing: ")
l1.listprint()

Output

Linked List: 
731
672
63
After reversing: 
Linked List: 
63
672
731

Search Operation

Searching for an element in the list using a key element. This operation is done in the same way as array search; comparing every element in the list with the key element given.

Algorithm

1 START
2 If the list is not empty, iteratively check if the list contains the key
3 If the key element is not present in the list, unsuccessful search
4 END

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;

// display the list
void printList(){
   struct node *p = head;
   printf("\n[");

   //start from the beginning
   while(p != NULL) {
      printf(" %d ",p->data);
      p = p->next;
   }
   printf("]");
}

//insertion at the beginning
void insertatbegin(int data){

   //create a link
   struct node *lk = (struct node*) malloc(sizeof(struct node));
   lk->data = data;

   // point it to old first node
   lk->next = head;

   //point first to new first node
   head = lk;
}
int searchlist(int key){
   struct node *temp = head;
   while(temp != NULL) {
      if (temp->data == key) {
         return 1;
      }
      temp=temp->next;
   }
   return 0;
}
void main(){
   int k=0;
   insertatbegin(12);
   insertatbegin(22);
   insertatbegin(30);
   insertatbegin(40);
   insertatbegin(55);
   printf("Linked List: ");

   // print list
   printList();
   k = searchlist(30);
   if (k == 1)
      printf("\nElement is found");
   else
      printf("\nElement is not present in the list");
}

Output

Linked List: 
[ 55  40  30  22  12 ]
Element is found

#include <bits/stdc++.h>
#include <string>
using namespace std;
struct node {
   int data;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;

// display the list
void printList(){
   struct node *p = head;
   cout << "\n[";

   //start from the beginning
   while(p != NULL) {
      cout << " " << p->data << " ";
      p = p->next;
   }
   cout << "]";
}

//insertion at the beginning
void insertatbegin(int data){

   //create a link
   struct node *lk = (struct node*) malloc(sizeof(struct node));
   lk->data = data;

   // point it to old first node
   lk->next = head;

   //point first to new first node
   head = lk;
}
int searchlist(int key){
   struct node *temp = head;
   while(temp != NULL) {
      if (temp->data == key) {
         return 1;
      }
      temp=temp->next;
   }
   return 0;
}
int main(){
   int k = 0;
   insertatbegin(12);
   insertatbegin(22);
   insertatbegin(30);
   insertatbegin(44);
   insertatbegin(50);
   cout << "Linked List: ";

   // print list
   printList();
   k = searchlist(16);
   if (k == 1)
      cout << "\nElement is found";
   else
      cout << "\nElement is not present in the list";
}

Output

Linked List: 
[ 50  44  30  22  12 ]
Element is not present in the list

public class Linked_List {
   static class node {
      int data;
      node next;
      node (int value) {
         data = value;
         next = null;
      }
   }
   static node head;

   // display the list
   static void printList() {
      node p = head;
      System.out.print("\n[");

      //start from the beginning
      while(p != null) {
         System.out.print(" " + p.data + " ");
         p = p.next;
      }
      System.out.print("]");
   }

   //insertion at the beginning
   static void insertatbegin(int data) {

      //create a link
      node lk = new node(data);;

      // point it to old first node
      lk.next = head;
      
      //point first to new first node
      head = lk;
   }
   static int searchlist(int key) {
      node temp = head;
      while(temp != null) {
         if (temp.data == key) {
            return 1;
         }
         temp=temp.next;
      }
      return 0;
   }
   public static void main(String args[]) {
      int k=0;
      insertatbegin(12);
      insertatbegin(22);
      insertatbegin(30);
      insertatbegin(44);
      insertatbegin(50);
      insertatbegin(33);
      System.out.println("Linked List: ");

      // print list
      printList();
      k = searchlist(44);
      if (k == 1)
         System.out.println("\nElement is found");
      else
         System.out.println("\nElement is not present in the list");
   }
}

Output

Linked List: 

[33  50  44  30  22  12 ]
Element is found

class Node:
   def __init__(self, data=None):
      self.data = data
      self.next = None

class SLL:
   def __init__(self):
      self.head = None
   def search(self, x):
      count = 0
      
      # Initialize current to head
      current = self.head

      # loop till current not equal to None
      while current != None:
         if current.data == x:
            print("data found")
            count = count + 1
         current = current.next
      if count == 0:
         print("Data Not found")

l1 = SLL()
l1.head = Node("731")
e2 = Node("672")
e3 = Node("63")

l1.head.next = e2
e2.next = e3

l1.search("63")

Output

data found

Traversal Operation

The traversal operation walks through all the elements of the list in an order and displays the elements in that order.

Algorithm

1. START
2. While the list is not empty and did not reach the end of the list, print the data in each node
3. END

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;

   // display the list
   void printList(){
   struct node *p = head;
   printf("\n[");

   //start from the beginning
   while(p != NULL) {
      printf(" %d ",p->data);
      p = p->next;
   }
   printf("]");
}

   //insertion at the beginning
   void insertatbegin(int data){

   //create a link
   struct node *lk = (struct node*) malloc(sizeof(struct node));
   lk->data = data;

   // point it to old first node
   lk->next = head;

   //point first to new first node
   head = lk;
}
void main(){
   int k=0;
   insertatbegin(12);
   insertatbegin(22);
   insertatbegin(30);
   printf("Linked List: ");

   // print list
   printList();
}

Output

Linked List: 
[ 30  22  12 ]

#include <bits/stdc++.h>
#include <string>
using namespace std;
struct node {
   int data;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;

// Displaying the list
void printList(){
   struct node *p = head;
   while(p != NULL) {
      cout << " " << p->data << " ";
      p = p->next;
   }
}

// Insertion at the beginning
void insertatbegin(int data){

   //create a link
   struct node *lk = (struct node*) malloc(sizeof(struct node));
   lk->data = data;

   // point it to old first node
   lk->next = head;

   //point first to new first node
   head = lk;
}
int main(){
   insertatbegin(12);
   insertatbegin(22);
   insertatbegin(30);
   insertatbegin(44);
   insertatbegin(50);
   cout << "Linked List: ";

   // print list
   printList();
}

Output

Linked List:  50  44  30  22  12

public class Linked_List {
   static class node {
      int data;
      node next;
      node (int value) {
         data = value;
         next = null;
      }
   }
   static node head;

   // display the list
   static void printList() {
      node p = head;
      System.out.print("\n[");
      
      //start from the beginning
      while(p != null) {
         System.out.print(" " + p.data + " ");
         p = p.next;
      }
      System.out.print("]");
   }
   
   //insertion at the beginning
   static void insertatbegin(int data) {

      //create a link
      node lk = new node(data);;

      // point it to old first node
      lk.next = head;

      //point first to new first node
      head = lk;
   }
   public static void main(String args[]) {
      int k=0;
      insertatbegin(12);
      insertatbegin(22);
      insertatbegin(30);
      insertatbegin(44);
      insertatbegin(50);
      insertatbegin(33);
      System.out.println("Linked List: ");

      // print list
      printList();
   }
}

Output

Linked List: 
[ 33  50  44  30  22  12 ]

class Node:
   def __init__(self, data=None):
      self.data = data
      self.next = None
class SLL:
   def __init__(self):
      self.head = None

# Print the linked list
   def listprint(self):
      printval = self.head
      print("Linked List: ")
      while printval is not None:
         print (printval.data)
         printval = printval.next

l1 = SLL()
l1.head = Node("731")
e2 = Node("672")
e3 = Node("63")

l1.head.next = e2
e2.next = e3

l1.listprint()

Output

Linked List: 
731
672
63

Implementation of Linked Lists

Let us look at the implementation of the linked list data structures below −

To know more about the linked list implementation of Linked Lists in C programming language, click here.

For the complete implementation of a Singly Linked List in C++ programming language, click here.

To learn more about the Java implementation of the Singly Linked Lists, click here.

To see the Python Implementation of the Singly Linked Lists, click here.

Data Structure Doubly Linked List

Doubly Linked List is a variation of Linked list in which navigation is possible in both ways, either forward and backward easily as compared to Single Linked List. Following are the important terms to understand the concept of doubly linked list.

Link − Each link of a linked list can store a data called an element.
Next − Each link of a linked list contains a link to the next link called Next.
Prev − Each link of a linked list contains a link to the previous link called Prev.
Linked List − A Linked List contains the connection link to the first link called First and to the last link called Last.

Doubly Linked List Representation

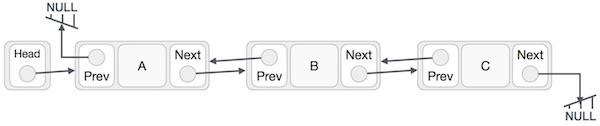
As per the above illustration, following are the important points to be considered.

Doubly Linked List contains a link element called first and last.
Each link carries a data field(s) and a link field called next.
Each link is linked with its next link using its next link.
Each link is linked with its previous link using its previous link.
The last link carries a link as null to mark the end of the list.

Basic Operations

Following are the basic operations supported by a list.

Insertion − Adds an element at the beginning of the list.
Deletion − Deletes an element at the beginning of the list.
Insert Last − Adds an element at the end of the list.
Delete Last − Deletes an element from the end of the list.
Insert After − Adds an element after an item of the list.
Delete − Deletes an element from the list using the key.
Display forward − Displays the complete list in a forward manner.
Display backward − Displays the complete list in a backward manner.

Insertion at the Beginning

In this operation, we create a new node with three compartments, one containing the data, the others containing the address of its previous and next nodes in the list. This new node is inserted at the beginning of the list.

Algorithm

1. START
2. Create a new node with three variables: prev, data, next.
3. Store the new data in the data variable
4. If the list is empty, make the new node as head.
5. Otherwise, link the address of the existing first node to the next variable of the new node, and assign null to the prev variable.
6. Point the head to the new node.
7. END

Example

Following are the implementations of this operation in various programming languages −

C C++

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
struct node {
   int data;
   int key;
   struct node *next;
   struct node *prev;
};

//this link always point to first Link
struct node *head = NULL;

//this link always point to last Link
struct node *last = NULL;
struct node *current = NULL;

//is list empty
bool isEmpty(){
   return head == NULL;
}

//display the doubly linked list
void printList(){
   struct node *ptr = head;
   while(ptr != NULL) {
      printf("(%d,%d) ",ptr->key,ptr->data);
      ptr = ptr->next;
   }
}

//insert link at the first location
void insertFirst(int key, int data){

   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data = data;
   if(isEmpty()) {

      //make it the last link
      last = link;
   } else {

      //update first prev link
      head->prev = link;
   }

   //point it to old first link
   link->next = head;

   //point first to new first link
   head = link;
}
void main(){
   insertFirst(1,10);
   insertFirst(2,20);
   insertFirst(3,30);
   insertFirst(4,1);
   insertFirst(5,40);
   insertFirst(6,56);
   printf("\nDoubly Linked List: ");
   printList();
}

Output

Doubly Linked List: (6,56) (5,40) (4,1) (3,30) (2,20) (1,10)

#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdbool>
struct node {
   int data;
   int key;
   struct node *next;
   struct node *prev;
};

//this link always point to first Link
struct node *head = NULL;

//this link always point to last Link
struct node *last = NULL;
struct node *current = NULL;

//is list empty
bool isEmpty(){
   return head == NULL;
}

//display the doubly linked list
void printList(){
   struct node *ptr = head;
   while(ptr != NULL) {
      printf("(%d,%d) ",ptr->key,ptr->data);
      ptr = ptr->next;
   }
}

//insert link at the first location
void insertFirst(int key, int data){

   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data = data;
   if(isEmpty()) {

      //make it the last link
      last = link;
   } else {

      //update first prev link
      head->prev = link;
   }

   //point it to old first link
   link->next = head;

   //point first to new first link
   head = link;
}
int main(){
   insertFirst(1,10);
   insertFirst(2,20);
   insertFirst(3,30);
   insertFirst(4,1);
   insertFirst(5,40);
   insertFirst(6,56);
   printf("\nDoubly Linked List: ");
   printList();
   return 0;
}

Output

Doubly Linked List: (6,56) (5,40) (4,1) (3,30) (2,20) (1,10)

Deletion at the Beginning

This deletion operation deletes the existing first nodes in the doubly linked list. The head is shifted to the next node and the link is removed.

Algorithm

1. START
2. Check the status of the doubly linked list
3. If the list is empty, deletion is not possible
4. If the list is not empty, the head pointer is shifted to the next node.
5. END

Example

Following are the implementations of this operation in various programming languages −

C C++

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
struct node {
   int data;
   int key;
   struct node *next;
   struct node *prev;
};

//this link always point to first Link
struct node *head = NULL;

//this link always point to last Link
struct node *last = NULL;
struct node *current = NULL;

//is list empty
bool isEmpty(){
   return head == NULL;
}

//display the doubly linked list
void printList(){
   struct node *ptr = head;
   while(ptr != NULL) {
      printf("(%d,%d) ",ptr->key,ptr->data);
      ptr = ptr->next;
   }
}

//insert link at the first location
void insertFirst(int key, int data){

   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data = data;
   if(isEmpty()) {

      //make it the last link
      last = link;
   } else {

      //update first prev link
      head->prev = link;
   }

   //point it to old first link
   link->next = head;

   //point first to new first link
   head = link;
}

//delete first item
struct node* deleteFirst(){

   //save reference to first link
   struct node *tempLink = head;

   //if only one link
   if(head->next == NULL) {
      last = NULL;
   } else {
      head->next->prev = NULL;
   }
   head = head->next;

   //return the deleted link
   return tempLink;
}
void main(){
   insertFirst(1,10);
   insertFirst(2,20);
   insertFirst(3,30);
   insertFirst(4,1);
   insertFirst(5,40);
   insertFirst(6,56);
   printf("\nDoubly Linked List: ");
   printList();
   printf("\nList after deleting first record: ");
   deleteFirst();
   printList();
}

Output

Doubly Linked List: (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) 
List after deleting first record: (5,40) (4,1) (3,30) (2,20) (1,10)

#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdbool>
struct node {
   int data;
   int key;
   struct node *next;
   struct node *prev;
};

//this link always point to first Link
struct node *head = NULL;

//this link always point to last Link
struct node *last = NULL;
struct node *current = NULL;

//is list empty
bool isEmpty(){
   return head == NULL;
}

//display the doubly linked list
void printList(){
   struct node *ptr = head;
   while(ptr != NULL) {
      printf("(%d,%d) ",ptr->key,ptr->data);
      ptr = ptr->next;
   }
}

//insert link at the first location
void insertFirst(int key, int data){

   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data = data;
   if(isEmpty()) {

      //make it the last link
      last = link;
   } else {

      //update first prev link
      head->prev = link;
   }

   //point it to old first link
   link->next = head;

   //point first to new first link
   head = link;
}

//delete first item
struct node* deleteFirst(){

   //save reference to first link
   struct node *tempLink = head;

   //if only one link
   if(head->next == NULL) {
      last = NULL;
   } else {
      head->next->prev = NULL;
   }
   head = head->next;

   //return the deleted link
   return tempLink;
}
int main(){
   insertFirst(1,10);
   insertFirst(2,20);
   insertFirst(3,30);
   insertFirst(4,1);
   insertFirst(5,40);
   insertFirst(6,56);
   printf("\nDoubly Linked List: ");
   printList();
   printf("\nList after deleting first record: ");
   deleteFirst();
   printList();
   return 0;
}

Output

Doubly Linked List: (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) 
List after deleting first record: (5,40) (4,1) (3,30) (2,20) (1,10)

Insertion at the End

In this insertion operation, the new input node is added at the end of the doubly linked list; if the list is not empty. The head will be pointed to the new node, if the list is empty.

Algorithm

1. START
2. If the list is empty, add the node to the list and point the head to it.
3. If the list is not empty, find the last node of the list.
4. Create a link between the last node in the list and the new node.
5. The new node will point to NULL as it is the new last node.
6. END

Example

Following are the implementations of this operation in various programming languages −

C C++

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
struct node {
   int data;
   int key;
   struct node *next;
   struct node *prev;
};

//this link always point to first Link
struct node *head = NULL;

//this link always point to last Link
struct node *last = NULL;
struct node *current = NULL;

//is list empty
bool isEmpty(){
   return head == NULL;
}

//display the doubly linked list
void printList(){
   struct node *ptr = head;
   while(ptr != NULL) {
      printf("(%d,%d) ",ptr->key,ptr->data);
      ptr = ptr->next;
   }
}

//insert link at the first location
void insertFirst(int key, int data){

   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data = data;
   if(isEmpty()) {

      //make it the last link
      last = link;
   } else {

      //update first prev link
      head->prev = link;
   }

   //point it to old first link
   link->next = head;

   //point first to new first link
   head = link;
}

//insert link at the last location
void insertLast(int key, int data){
   
   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data = data;
   if(isEmpty()) {

      //make it the last link
      last = link;
   } else {

      //make link a new last link
      last->next = link;

      //mark old last node as prev of new link
      link->prev = last;
   }

   //point last to new last node
   last = link;
}
void main(){
   insertFirst(1,10);
   insertFirst(2,20);
   insertFirst(3,30);
   insertFirst(4,1);
   insertLast(5,40);
   insertLast(6,56);
   printf("\nDoubly Linked List: ");
   printList();
}

Output

Doubly Linked List: (4,1) (3,30) (2,20) (1,10) (5,40) (6,56)

#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdbool>
struct node {
   int data;
   int key;
   struct node *next;
   struct node *prev;
};

//this link always point to first Link
struct node *head = NULL;

//this link always point to last Link
struct node *last = NULL;
struct node *current = NULL;

//is list empty
bool isEmpty(){
   return head == NULL;
}

//display the doubly linked list
void printList(){
   struct node *ptr = head;
   while(ptr != NULL) {
      printf("(%d,%d) ",ptr->key,ptr->data);
      ptr = ptr->next;
   }
}

//insert link at the first location
void insertFirst(int key, int data){

   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data = data;
   if(isEmpty()) {

      //make it the last link
      last = link;
   } else {

      //update first prev link
      head->prev = link;
   }

   //point it to old first link
   link->next = head;

   //point first to new first link
   head = link;
}

//insert link at the last location
void insertLast(int key, int data){

   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data = data;
   if(isEmpty()) {

      //make it the last link
      last = link;
   } else {

      //make link a new last link
      last->next = link;

      //mark old last node as prev of new link
      link->prev = last;
   }

   //point last to new last node
   last = link;
}
int main(){
   insertFirst(1,10);
   insertFirst(2,20);
   insertFirst(3,30);
   insertFirst(4,1);
   insertLast(5,40);
   insertLast(6,56);
   printf("\nDoubly Linked List: ");
   printList();
   return 0;
}

Output

Doubly Linked List: (4,1) (3,30) (2,20) (1,10) (5,40) (6,56)

To see the implementation in C programming language, please click here.

To learn more about the doubly linked list operations with the help of C++ implementation, click here.

Data Structure - Circular Linked List

Circular Linked List is a variation of Linked list in which the first element points to the last element and the last element points to the first element. Both Singly Linked List and Doubly Linked List can be made into a circular linked list.

Singly Linked List as Circular

In singly linked list, the next pointer of the last node points to the first node.

Doubly Linked List as Circular

In doubly linked list, the next pointer of the last node points to the first node and the previous pointer of the first node points to the last node making the circular in both directions.

As per the above illustration, following are the important points to be considered.

The last link's next points to the first link of the list in both cases of singly as well as doubly linked list.
The first link's previous points to the last of the list in case of doubly linked list.

Basic Operations

Following are the important operations supported by a circular list.

insert − Inserts an element at the start of the list.
delete − Deletes an element from the start of the list.
display − Displays the list.

Insertion Operation

The insertion operation of a circular linked list only inserts the element at the start of the list. This differs from the usual singly and doubly linked lists as there is no particular starting and ending points in this list. The insertion is done either at the start or after a particular node (or a given position) in the list.

Algorithm

1. START
2. Check if the list is empty
3. If the list is empty, add the node and point the head to this node
4. If the list is not empty, link the existing head as the next node to the new node.
5. Make the new node as the new head.
6. END

Example

Following are the implementations of this operation in various programming languages −

C C++

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
struct node {
   int data;
   int key;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
bool isEmpty(){
   return head == NULL;
}

//insert link at the first location
void insertFirst(int key, int data){

   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data = data;
   if (isEmpty()) {
      head = link;
      head->next = head;
   } else {

      //point it to old first node
      link->next = head;

      //point first to new first node
      head = link;
   }
}

//display the list
void printList(){
   struct node *ptr = head;
   printf("\n[ ");

   //start from the beginning
   if(head != NULL) {
      while(ptr->next != ptr) {
         printf("(%d,%d) ",ptr->key,ptr->data);
         ptr = ptr->next;
      }
   }
   printf(" ]");
}
void main(){
   insertFirst(1,10);
   insertFirst(2,20);
   insertFirst(3,30);
   insertFirst(4,1);
   insertFirst(5,40);
   insertFirst(6,56);
   printf("Circular Linked List: ");

   //print list
   printList();
}

Output

Circular Linked List: 
[ (6,56) (5,40) (4,1) (3,30) (2,20)  ]

#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdbool>
struct node {
   int data;
   int key;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
bool isEmpty(){
   return head == NULL;
}
//insert link at the first location
void insertFirst(int key, int data){

   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data = data;
   if (isEmpty()) {
      head = link;
      head->next = head;
   } else {

      //point it to old first node
      link->next = head;

      //point first to new first node
      head = link;
   }
}

//display the list
void printList(){
   struct node *ptr = head;
   printf("\n[ ");

   //start from the beginning
   if(head != NULL) {
      while(ptr->next != ptr) {
         printf("(%d,%d) ",ptr->key,ptr->data);
         ptr = ptr->next;
      }
   }
   printf(" ]");
}
int main(){
   insertFirst(1,10);
   insertFirst(2,20);
   insertFirst(3,30);
   insertFirst(4,1);
   insertFirst(5,40);
   insertFirst(6,56);
   printf("Circular Linked List: ");
   
   //print list
   printList();
   return 0;
}

Output

Circular Linked List: 
[ (6,56) (5,40) (4,1) (3,30) (2,20)  ]

Deletion Operation

The Deletion operation in a Circular linked list removes a certain node from the list. The deletion operation in this type of lists can be done at the beginning, or a given position, or at the ending.

Algorithm

1. START
2. If the list is empty, then the program is returned.
3. If the list is not empty, we traverse the list using a current pointer that is set to the head pointer and create another pointer previous that points to the last node.
4. Suppose the list has only one node, the node is deleted by setting the head pointer to NULL.
5. If the list has more than one node and the first node is to be deleted, the head is set to the next node and the previous is linked to the new head.
6. If the node to be deleted is the last node, link the preceding node of the last node to head node.
7. If the node is neither first nor last, remove the node by linking its preceding node to its succeeding node.
8. END

Example

Following are the implementations of this operation in various programming languages −

C C++

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
struct node {
   int data;
   int key;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
bool isEmpty(){
   return head == NULL;
}

//insert link at the first location
void insertFirst(int key, int data){

   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data = data;
   if (isEmpty()) {
      head = link;
      head->next = head;
   } else {

      //point it to old first node
      link->next = head;

      //point first to new first node
      head = link;
   }
}

//delete first item
struct node * deleteFirst(){

   //save reference to first link
   struct node *tempLink = head;
   if(head->next == head) {
      head = NULL;
      return tempLink;
   }

   //mark next to first link as first
   head = head->next;

   //return the deleted link
   return tempLink;
}

//display the list
void printList(){
   struct node *ptr = head;

   //start from the beginning
   if(head != NULL) {
      while(ptr->next != ptr) {
         printf("(%d,%d) ",ptr->key,ptr->data);
         ptr = ptr->next;
      }
   }
}
void main(){
   insertFirst(1,10);
   insertFirst(2,20);
   insertFirst(3,30);
   insertFirst(4,1);
   insertFirst(5,40);
   insertFirst(6,56);
   printf("Circular Linked List: ");

   //print list
   printList();
   deleteFirst();
   printf("\nList after deleting the first item: ");
   printList();
}

Output

Circular Linked List: (6,56) (5,40) (4,1) (3,30) (2,20) 
List after deleting the first item: (5,40) (4,1) (3,30) (2,20)

#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdbool>
struct node {
   int data;
   int key;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
bool isEmpty(){
   return head == NULL;
}

//insert link at the first location
void insertFirst(int key, int data){

   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data = data;
   if (isEmpty()) {
      head = link;
      head->next = head;
   } else {

      //point it to old first node
      link->next = head;

      //point first to new first node
      head = link;
   }
}

//delete first item
struct node * deleteFirst(){
   
   //save reference to first link
   struct node *tempLink = head;
   if(head->next == head) {
      head = NULL;
      return tempLink;
   }

   //mark next to first link as first
   head = head->next;

   //return the deleted link
   return tempLink;
}

//display the list
void printList(){
   struct node *ptr = head;

   //start from the beginning
   if(head != NULL) {
      while(ptr->next != ptr) {
         printf("(%d,%d) ",ptr->key,ptr->data);
         ptr = ptr->next;
      }
   }
}
int main(){
   insertFirst(1,10);
   insertFirst(2,20);
   insertFirst(3,30);
   insertFirst(4,1);
   insertFirst(5,40);
   insertFirst(6,56);
   printf("Circular Linked List: ");

   //print list
   printList();
   deleteFirst();
   printf("\nList after deleting the first item: ");
   printList();
   return 0;
}

Output

Circular Linked List: (6,56) (5,40) (4,1) (3,30) (2,20) 
List after deleting the first item: (5,40) (4,1) (3,30) (2,20)

Display List Operation

The Display List operation visits every node in the list and prints them all in the output.

Algorithm

1. START
2. Walk through all the nodes of the list and print them
3. END

Example

Following are the implementations of this operation in various programming languages −

C C++

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
struct node {
   int data;
   int key;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
bool isEmpty(){
   return head == NULL;
}

//insert link at the first location
void insertFirst(int key, int data){

   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data = data;
   if (isEmpty()) {
      head = link;
      head->next = head;
   } else {

      //point it to old first node
      link->next = head;

      //point first to new first node
      head = link;
   }
}

//display the list
void printList(){
   struct node *ptr = head;
   printf("\n[ ");

   //start from the beginning
   if(head != NULL) {
      while(ptr->next != ptr) {
         printf("(%d,%d) ",ptr->key,ptr->data);
         ptr = ptr->next;
      }
   }
   printf(" ]");
}
void main(){
   insertFirst(1,10);
   insertFirst(2,20);
   insertFirst(3,30);
   insertFirst(4,1);
   insertFirst(5,40);
   insertFirst(6,56);
   printf("Circular Linked List: ");

   //print list
   printList();
}

Output

Circular Linked List: 
[ (6,56) (5,40) (4,1) (3,30) (2,20)  ]

#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdbool>
struct node {
   int data;
   int key;
   struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
bool isEmpty(){
   return head == NULL;
}

//insert link at the first location
void insertFirst(int key, int data){
   
   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data = data;
   if (isEmpty()) {
      head = link;
      head->next = head;
   } else {

      //point it to old first node
      link->next = head;

      //point first to new first node
      head = link;
   }
}

//display the list
void printList(){
   struct node *ptr = head;
   printf("\n[ ");

   //start from the beginning
   if(head != NULL) {
      while(ptr->next != ptr) {
         printf("(%d,%d) ",ptr->key,ptr->data);
         ptr = ptr->next;
      }
   }
   printf(" ]");
}
int main(){
   insertFirst(1,10);
   insertFirst(2,20);
   insertFirst(3,30);
   insertFirst(4,1);
   insertFirst(5,40);
   insertFirst(6,56);
   printf("Circular Linked List: ");

   //print list
   printList();
   return 0;
}

Output

Circular Linked List: 
[ (6,56) (5,40) (4,1) (3,30) (2,20)  ]

To know about its implementation in C programming language, please click here.

To know more about the C++ implementation of the circular linked list, click here.

Data Structure and Algorithms - Stack

A stack is an Abstract Data Type (ADT), that is popularly used in most programming languages. It is named stack because it has the similar operations as the real-world stacks, for example – a pack of cards or a pile of plates, etc.

The stack follows the LIFO (Last in - First out) structure where the last element inserted would be the first element deleted.

Stack Representation

A Stack ADT allows all data operations at one end only. At any given time, we can only access the top element of a stack.

The following diagram depicts a stack and its operations −

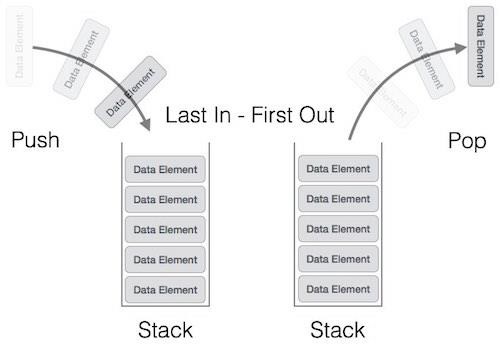
A stack can be implemented by means of Array, Structure, Pointer, and Linked List. Stack can either be a fixed size one or it may have a sense of dynamic resizing. Here, we are going to implement stack using arrays, which makes it a fixed size stack implementation.

Basic Operations on Stacks

Stack operations usually are performed for initialization, usage and, de-initialization of the stack ADT.

The most fundamental operations in the stack ADT include: push(), pop(), peek(), isFull(), isEmpty(). These are all built-in operations to carry out data manipulation and to check the status of the stack.

Stack uses pointers that always point to the topmost element within the stack, hence called as the top pointer.

Insertion: push()

push() is an operation that inserts elements into the stack. The following is an algorithm that describes the push() operation in a simpler way.

Algorithm

1 − Checks if the stack is full.
2 − If the stack is full, produces an error and exit.
3 − If the stack is not full, increments top to point next empty space.
4 − Adds data element to the stack location, where top is pointing.
5 − Returns success.

Example

Following are the implementations of this operation in various programming languages −

C C++ Java

#include <stdio.h>
int MAXSIZE = 8;
int stack[8];
int top = -1;

/* Check if the stack is full*/
int isfull(){
   if(top == MAXSIZE)
      return 1;
   else
      return 0;
}

/* Function to insert into the stack */
int push(int data){
   if(!isfull()) {
      top = top + 1;
      stack[top] = data;
   } else {
      printf("Could not insert data, Stack is full.\n");
   }
}

/* Main function */
int main(){
   int i;
   push(44);
   push(10);
   push(62);
   push(123);
   push(15);
   printf("Stack Elements: \n");
   
   // print stack data
   for(i = 0; i < 8; i++) {
      printf("%d ", stack[i]);
   }
   return 0;
}

Output

Stack Elements: 
44 10 62 123 15 0 0 0

#include <iostream>
int MAXSIZE = 8;
int stack[8];
int top = -1;

/* Check if the stack is full*/
int isfull(){
   if(top == MAXSIZE)
      return 1;
   else
      return 0;
}

/* Function to insert into the stack */
int push(int data){
   if(!isfull()) {
      top = top + 1;
      stack[top] = data;
   } else {
      printf("Could not insert data, Stack is full.\n");
   }
}

/* Main function */
int main(){
   int i;
   push(44);
   push(10);
   push(62);
   push(123);
   push(15);
   printf("Stack Elements: \n");

   // print stack data
   for(i = 0; i < 8; i++) {
      printf("%d ", stack[i]);
   }
   return 0;
}

Output

Stack Elements: 
44 10 62 123 15 0 0 0

import java.io.*;
import java.util.*; // util imports the stack class
public class StackExample {
   public static void main (String[] args) {
      Stack<Integer> stk = new Stack<Integer>();
      
      // inserting elements into the stack
      stk.push(52);
      stk.push(19);
      stk.push(33);
      stk.push(14);
      stk.push(6);
      System.out.print("The stack is: " + stk);
   }
}

Output

The stack is: [52, 19, 33, 14, 6]

class Stack:
   def __init__(self):
      self.stack = []
   def __str__(self):
      return str(self.stack)
   def push(self, data):
      if data not in self.stack:
         self.stack.append(data)
         return True
      else:
         return False
stk = Stack()
stk.push(1)
stk.push(2)
stk.push(3)
stk.push(4)
stk.push(5)
print("Stack Elements:")
print(stk)

Output

Stack Elements:
[1, 2, 3, 4, 5]

Note − In Java we have used to built-in method push() to perform this operation.

Deletion: pop()

pop() is a data manipulation operation which removes elements from the stack. The following pseudo code describes the pop() operation in a simpler way.

Algorithm

1 − Checks if the stack is empty.
2 − If the stack is empty, produces an error and exit.
3 − If the stack is not empty, accesses the data element at which top is pointing.
4 − Decreases the value of top by 1.
5 − Returns success.

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
int MAXSIZE = 8;
int stack[8];
int top = -1;

/* Check if the stack is empty */
int isempty(){
   if(top == -1)
      return 1;
   else
      return 0;
}

/* Check if the stack is full*/
int isfull(){
   if(top == MAXSIZE)
      return 1;
   else
      return 0;
}

/* Function to delete from the stack */
int pop(){
   int data;
   if(!isempty()) {
      data = stack[top];
      top = top - 1;
      return data;
   } else {
      printf("Could not retrieve data, Stack is empty.\n");
   }
}

/* Function to insert into the stack */
int push(int data){
   if(!isfull()) {
      top = top + 1;
      stack[top] = data;
   } else {
      printf("Could not insert data, Stack is full.\n");
   }
}

/* Main function */
int main(){
   int i;
   push(44);
   push(10);
   push(62);
   push(123);
   push(15);
   printf("Stack Elements: \n");

   // print stack data
   for(i = 0; i < 8; i++) {
      printf("%d ", stack[i]);
   }
   /*printf("Element at top of the stack: %d\n" ,peek());*/
   printf("\nElements popped: \n");

   // print stack data
   while(!isempty()) {
      int data = pop();
      printf("%d ",data);
   }
   return 0;
}

Output

Stack Elements: 
44 10 62 123 15 0 0 0 
Elements popped: 
15 123 62 10 44

#include <iostream>
int MAXSIZE = 8;
int stack[8];
int top = -1;

/* Check if the stack is empty */
int isempty(){
   if(top == -1)
      return 1;
   else
      return 0;
}

/* Check if the stack is full*/
int isfull(){
   if(top == MAXSIZE)
      return 1;
   else
      return 0;
}

/* Function to delete from the stack */
int pop(){
   int data;
   if(!isempty()) {
      data = stack[top];
      top = top - 1;
      return data;
   } else {
      printf("Could not retrieve data, Stack is empty.\n");
   }
}

/* Function to insert into the stack */
int push(int data){
   if(!isfull()) {
      top = top + 1;
      stack[top] = data;
   } else {
      printf("Could not insert data, Stack is full.\n");
   }
}

/* Main function */
int main(){
   int i;
   push(44);
   push(10);
   push(62);
   push(123);
   push(15);
   printf("Stack Elements: \n");

   // print stack data
   for(i = 0; i < 8; i++) {
      printf("%d ", stack[i]);
   }
   
   /*printf("Element at top of the stack: %d\n" ,peek());*/
   printf("\nElements popped: \n");

   // print stack data
   while(!isempty()) {
      int data = pop();
      printf("%d ",data);
   }
   return 0;
}

Output

Stack Elements: 
44 10 62 123 15 0 0 0 
Elements popped: 
15 123 62 10 44

import java.io.*;
import java.util.*; 

// util imports the stack class
public class StackExample {
   public static void main (String[] args) {
      Stack<Integer> stk = new Stack<Integer>();
      
      // Inserting elements into the stack
      stk.push(52);
      stk.push(19);
      stk.push(33);
      stk.push(14);
      stk.push(6);
      System.out.print("The stack is: " + stk);
      
      // Deletion from the stack
      System.out.print("\nThe popped element is: ");
      Integer n = (Integer) stk.pop();
      System.out.print(n);
   }
}

Output

The stack is: [52, 19, 33, 14, 6]
The popped element is: 6

class Stack:
   def __init__(self):
      self.stack = []
   def __str__(self):
      return str(self.stack)
   def push(self, data):
      if data not in self.stack:
         self.stack.append(data)
         return True
      else:
         return False
   def remove(self):
      if len(self.stack) <= 0:
         return ("No element in the Stack")
      else:
         return self.stack.pop()
stk = Stack()
stk.push(1)
stk.push(2)
stk.push(3)
stk.push(4)
stk.push(5)
print("Stack Elements:")
print(stk)
print("----Deletion operation in stack----")
p = stk.remove()
print("The popped element is: " + str(p))
print("Updated Stack:")
print(stk)

Output

Stack Elements:
[1, 2, 3, 4, 5]
----Deletion operation in stack----
The popped element is: 5
Updated Stack:
[1, 2, 3, 4]

Note − In Java we are using the built-in method pop().

peek()

The peek() is an operation retrieves the topmost element within the stack, without deleting it. This operation is used to check the status of the stack with the help of the top pointer.

Algorithm

1. START
2. return the element at the top of the stack
3. END

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
int MAXSIZE = 8;
int stack[8];
int top = -1;

/* Check if the stack is full */
int isfull(){
   if(top == MAXSIZE)
      return 1;
   else
      return 0;
}

/* Function to return the topmost element in the stack */
int peek(){
   return stack[top];
}

/* Function to insert into the stack */
int push(int data){
   if(!isfull()) {
      top = top + 1;
      stack[top] = data;
   } else {
      printf("Could not insert data, Stack is full.\n");
   }
}

/* Main function */
int main(){
   int i;
   push(44);
   push(10);
   push(62);
   push(123);
   push(15);
   printf("Stack Elements: \n");

   // print stack data
   for(i = 0; i < 8; i++) {
      printf("%d ", stack[i]);
   }
   printf("\nElement at top of the stack: %d\n" ,peek());
   return 0;
}

Output

Stack Elements: 
44 10 62 123 15 0 0 0 
Element at top of the stack: 15

#include <iostream>
int MAXSIZE = 8;
int stack[8];
int top = -1;

/* Check if the stack is full */
int isfull(){
   if(top == MAXSIZE)
      return 1;
   else
      return 0;
}

/* Function to return the topmost element in the stack */
int peek(){
   return stack[top];
}

/* Function to insert into the stack */
int push(int data){
   if(!isfull()) {
      top = top + 1;
      stack[top] = data;
   } else {
      printf("Could not insert data, Stack is full.\n");
   }
}

/* Main function */
int main(){
   int i;
   push(44);
   push(10);
   push(62);
   push(123);
   push(15);
   printf("Stack Elements: \n");

   // print stack data
   for(i = 0; i < 8; i++) {
      printf("%d ", stack[i]);
   }
   printf("\nElement at top of the stack: %d\n" ,peek());
   return 0;
}

Output

Stack Elements: 
44 10 62 123 15 0 0 0 
Element at top of the stack: 15

import java.io.*;
import java.util.*; 

// util imports the stack class
public class StackExample {
   public static void main (String[] args) {
      Stack<Integer> stk = new Stack<Integer>();
      
      // inserting elements into the stack
      stk.push(52);
      stk.push(19);
      stk.push(33);
      stk.push(14);
      stk.push(6);
      System.out.print("The stack is: " + stk);
      Integer pos = (Integer) stk.peek();
      System.out.print("\nThe element found is " + pos);
   }
}

Output

The stack is: [52, 19, 33, 14, 6]
The element found is 6

class Stack:
   def __init__(self):
      self.stack = []
   def __str__(self):
      return str(self.stack)
   def push(self, data):
      if data not in self.stack:
         self.stack.append(data)
         return True
      else:
         return False
   # Use peek to look at the top of the stack
   def peek(self):
      return self.stack[-1]
stk = Stack()
stk.push(1)
stk.push(2)
stk.push(3)
stk.push(4)
stk.push(5)
print("Stack Elements:")
print(stk)
print("topmost element: ",stk.peek())

Output

Stack Elements:
[1, 2, 3, 4, 5]
topmost element: 5

isFull()

isFull() operation checks whether the stack is full. This operation is used to check the status of the stack with the help of top pointer.

Algorithm

1. START
2. If the size of the stack is equal to the top position of the stack, the stack is full. Return 1.
3. Otherwise, return 0.
4. END

Example

Following are the implementations of this operation in various programming languages −

C C++ Java

#include <stdio.h>
int MAXSIZE = 8;
int stack[8];
int top = -1;

/* Check if the stack is full */
int isfull(){
   if(top == MAXSIZE)
      return 1;
   else
      return 0;
}

/* Main function */
int main(){
   printf("Stack full: %s\n" , isfull()?"true":"false");
   return 0;
}

Output

Stack full: false

#include <iostream>
int MAXSIZE = 8;
int stack[8];
int top = -1;

/* Check if the stack is full */
int isfull(){
   if(top == MAXSIZE)
      return 1;
   else
      return 0;
}

/* Main function */
int main(){
   printf("Stack full: %s\n" , isfull()?"true":"false");
   return 0;
}

Output

Stack full: false

import java.io.*;
public class StackExample {
   private int arr[];
   private int top;
   private int capacity;
   StackExample(int size) {
      arr = new int[size];
      capacity = size;
      top = -1;
   }
   public boolean isEmpty() {
      return top == -1;
   }
   public boolean isFull() {
      return top == capacity - 1;
   }
   public void push(int key) {
      if (isFull()) {
         System.out.println("Stack is Full\n");
         return;
      }
      arr[++top] = key;
   }
   public static void main (String[] args) {
      StackExample stk = new StackExample(5);
      stk.push(1); // inserting 1 in the stack
      stk.push(2);
      stk.push(3);
      stk.push(4);
      stk.push(5);
      System.out.println("Stack Full? " + stk.isFull());
   }
}

Output

Stack Full? true

isEmpty()

The isEmpty() operation verifies whether the stack is empty. This operation is used to check the status of the stack with the help of top pointer.

Algorithm

1. START
2. If the top value is -1, the stack is empty. Return 1.
3. Otherwise, return 0.
4. END

Example

Following are the implementations of this operation in various programming languages −

C C++ Java

#include <stdio.h>
int MAXSIZE = 8;
int stack[8];
int top = -1;

/* Check if the stack is empty */
int isempty() {
   if(top == -1)
      return 1;
   else
      return 0;
}

/* Main function */
int main() {
   printf("Stack empty: %s\n" , isempty()?"true":"false");
   return 0;
}

Output

Stack empty: true

#include <iostream>
int MAXSIZE = 8;
int stack[8];
int top = -1;

/* Check if the stack is empty */
int isempty(){
   if(top == -1)
      return 1;
   else
      return 0;
}

/* Main function */
int main(){
   printf("Stack empty: %s\n" , isempty()?"true":"false");
   return 0;
}

Output

Stack empty: true

import java.io.*;
import java.util.*; // util imports the stack class
public class StackExample {
   public static void main (String[] args) {
      Stack<Integer> stk = new Stack<Integer>();
      
      // Inserting elements into the stack
      stk.push(52);
      stk.push(19);
      stk.push(33);
      stk.push(14);
      stk.push(6);
      System.out.println("Stack empty? "+ stk.isEmpty());
   }
}

Output

Stack empty? false

Implementation of Stack

For a complete stack program in C programming language, please click here.

For a complete stack program in C++ programming language, please click here.

For a complete stack program in JAVA programming language, please click here.

For a complete stack program in Python programming language, please click here.

Data Structure - Expression Parsing

The way to write arithmetic expression is known as a notation. An arithmetic expression can be written in three different but equivalent notations, i.e., without changing the essence or output of an expression. These notations are −

Infix Notation
Prefix (Polish) Notation
Postfix (Reverse-Polish) Notation

These notations are named as how they use operator in expression. We shall learn the same here in this chapter.

Infix Notation

We write expression in infix notation, e.g. a - b + c, where operators are used in-between operands. It is easy for us humans to read, write, and speak in infix notation but the same does not go well with computing devices. An algorithm to process infix notation could be difficult and costly in terms of time and space consumption.

Prefix Notation

In this notation, operator is prefixed to operands, i.e. operator is written ahead of operands. For example, +ab. This is equivalent to its infix notation a + b. Prefix notation is also known as Polish Notation.

Postfix Notation

This notation style is known as Reversed Polish Notation. In this notation style, the operator is postfixed to the operands i.e., the operator is written after the operands. For example, ab+. This is equivalent to its infix notation a + b.

The following table briefly tries to show the difference in all three notations −

Sr.No.	Infix Notation	Prefix Notation	Postfix Notation
1	a + b	+ a b	a b +
2	(a + b) ∗ c	∗ + a b c	a b + c ∗
3	a ∗ (b + c)	∗ a + b c	a b c + ∗
4	a / b + c / d	+ / a b / c d	a b / c d / +
5	(a + b) ∗ (c + d)	∗ + a b + c d	a b + c d + ∗
6	((a + b) ∗ c) - d	- ∗ + a b c d	a b + c ∗ d -

Parsing Expressions

As we have discussed, it is not a very efficient way to design an algorithm or program to parse infix notations. Instead, these infix notations are first converted into either postfix or prefix notations and then computed.

To parse any arithmetic expression, we need to take care of operator precedence and associativity also.

Precedence

When an operand is in between two different operators, which operator will take the operand first, is decided by the precedence of an operator over others. For example −

As multiplication operation has precedence over addition, b * c will be evaluated first. A table of operator precedence is provided later.

Associativity

Associativity describes the rule where operators with the same precedence appear in an expression. For example, in expression a + b − c, both + and – have the same precedence, then which part of the expression will be evaluated first, is determined by associativity of those operators. Here, both + and − are left associative, so the expression will be evaluated as (a + b) − c.

Precedence and associativity determines the order of evaluation of an expression. Following is an operator precedence and associativity table (highest to lowest) −

Sr.No.	Operator	Precedence	Associativity
1	Exponentiation ^	Highest	Right Associative
2	Multiplication ( ∗ ) & Division ( / )	Second Highest	Left Associative
3	Addition ( + ) & Subtraction ( − )	Lowest	Left Associative

The above table shows the default behavior of operators. At any point of time in expression evaluation, the order can be altered by using parenthesis. For example −

In a + b*c, the expression part b*c will be evaluated first, with multiplication as precedence over addition. We here use parenthesis for a + b to be evaluated first, like (a + b)*c.

Postfix Evaluation Algorithm

We shall now look at the algorithm on how to evaluate postfix notation −

Step 1 − scan the expression from left to right 
Step 2 − if it is an operand push it to stack 
Step 3 − if it is an operator pull operand from stack and perform operation 
Step 4 − store the output of step 3, back to stack 
Step 5 − scan the expression until all operands are consumed 
Step 6 − pop the stack and perform operation

To see the implementation in C programming language, please click here.

Data Structure and Algorithms - Queue

Queue, like Stack, is also an abstract data structure. The thing that makes queue different from stack is that a queue is open at both its ends. Hence, it follows FIFO (First-In-First-Out) structure, i.e. the data item inserted first will also be accessed first. The data is inserted into the queue through one end and deleted from it using the other end.

A real-world example of queue can be a single-lane one-way road, where the vehicle enters first, exits first. More real-world examples can be seen as queues at the ticket windows and bus-stops.

Representation of Queues

Similar to the stack ADT, a queue ADT can also be implemented using arrays, linked lists, or pointers. As a small example in this tutorial, we implement queues using a one-dimensional array.

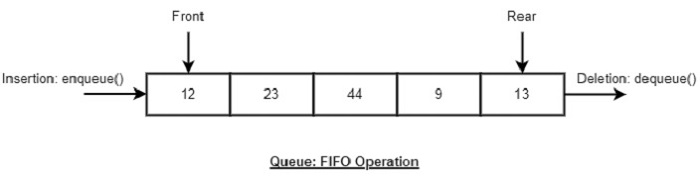
Basic Operations

Queue operations also include initialization of a queue, usage and permanently deleting the data from the memory.

The most fundamental operations in the queue ADT include: enqueue(), dequeue(), peek(), isFull(), isEmpty(). These are all built-in operations to carry out data manipulation and to check the status of the queue.

Queue uses two pointers − front and rear. The front pointer accesses the data from the front end (helping in enqueueing) while the rear pointer accesses data from the rear end (helping in dequeuing).

Insertion operation: enqueue()

The enqueue() is a data manipulation operation that is used to insert elements into the stack. The following algorithm describes the enqueue() operation in a simpler way.

Algorithm

1 − START
2 – Check if the queue is full.
3 − If the queue is full, produce overflow error and exit.
4 − If the queue is not full, increment rear pointer to point the next empty space.
5 − Add data element to the queue location, where the rear is pointing.
6 − return success.
7 – END

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
bool isEmpty(){
   return itemCount == 0;
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      printf("%d ",n);
   }
}

Output

Queue: 3 5 9 1 12 15

#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
bool isEmpty(){
   return itemCount == 0;
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      printf("%d ",n);
   }
}

Output

Queue: 3 5 9 1 12 15

import java.util.LinkedList;
import java.util.Queue;
public class QueueExample {
   public static void main(String[] args) {
      Queue<Integer> q = new LinkedList<>();
      q.add(6);
      q.add(1);
      q.add(8);
      q.add(4);
      q.add(7);
      System.out.println("The queue is: " + q);
   }
}

Output

The queue is: [6, 1, 8, 4, 7]

class Queue:
   def __init__(self):
      self.queue = list()
   def __str__(self):
      return str(self.queue)
   def addtoqueue(self,data):

   # Insert method to add element
      if data not in self.queue:
         self.queue.insert(0,data)
         return True
      return False

q = Queue()
q.addtoqueue("36")
q.addtoqueue("24")
q.addtoqueue("48")
q.addtoqueue("12")
q.addtoqueue("66")
print("Queue:")
print(q)

Output

Queue:
['66', '12', '48', '24', '36']

Deletion Operation: dequeue()

The dequeue() is a data manipulation operation that is used to remove elements from the stack. The following algorithm describes the dequeue() operation in a simpler way.

Algorithm

1 – START
2 − Check if the queue is empty.
3 − If the queue is empty, produce underflow error and exit.
4 − If the queue is not empty, access the data where front is pointing.
5 − Increment front pointer to point to the next available data element.
6 − Return success.
7 – END

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
bool isEmpty(){
   return itemCount == 0;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
int main(){
   int i;
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);

   // remove one item
   int num = removeData();
   printf("\nElement removed: %d\n",num);
   printf("Updated Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      printf("%d ",n);
   }
}

Output

Queue: 3 5 9 1 12 15 
Element removed: 3
Updated Queue: 5 9 1 12 15

#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
bool isEmpty(){
   return itemCount == 0;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
int main(){
   int i;
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   
   // remove one item
   int num = removeData();
   printf("\nElement removed: %d\n",num);
   printf("Updated Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      printf("%d ",n);
   }
}

Output

Queue: 3 5 9 1 12 15 
Element removed: 3
Updated Queue: 5 9 1 12 15

import java.util.LinkedList;
import java.util.Queue;
public class QueueExample {
   public static void main(String[] args) {
      Queue<Integer> q = new LinkedList<>();
      q.add(6);
      q.add(1);
      q.add(8);
      q.add(4);
      q.add(7);
      System.out.println("The queue is: " + q);
      int n = q.remove();
      System.out.println("The element deleted is: " + n);
      System.out.println("Queue after deletion: " + q);
   }
}

Output

The queue is: [6, 1, 8, 4, 7]
The element deleted is: 6
Queue after deletion: [1, 8, 4, 7]

class Queue:
   def __init__(self):
      self.queue = list()
   def __str__(self):
      return str(self.queue)
   def addtoqueue(self,data):

   # Insert method to add element
      if data not in self.queue:
         self.queue.insert(0,data)
         return True
      return False
   def removefromqueue(self):
      if len(self.queue)>0:
         return self.queue.pop()
      return ("Queue is empty")

q = Queue()
q.addtoqueue("36")
q.addtoqueue("24")
q.addtoqueue("48")
q.addtoqueue("12")
q.addtoqueue("66")
print("Queue:")
print(q)
print("Element deleted from queue: ",q.removefromqueue())

Output

Queue:
['66', '12', '48', '24', '36']
Element deleted from queue:  36

The peek() Operation

The peek() is an operation which is used to retrieve the frontmost element in the queue, without deleting it. This operation is used to check the status of the queue with the help of the pointer.

Algorithm

1 – START
2 – Return the element at the front of the queue
3 – END

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
   return intArray[front];
}
bool isFull(){
   return itemCount == MAX;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   int i;
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\nElement at front: %d\n",peek());
}

Output

Queue: 3 5 9 1 12 15 
Element at front: 3

#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
   return intArray[front];
}
bool isFull(){
   return itemCount == MAX;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   int i;
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\nElement at front: %d\n",peek());
}

Output

Queue: 3 5 9 1 12 15 
Element at front: 3

import java.util.LinkedList;
import java.util.Queue;
public class QueueExample {
   public static void main(String[] args) {
      Queue<Integer> q = new LinkedList<>();
      q.add(6);
      q.add(1);
      q.add(8);
      q.add(4);
      q.add(7);
      System.out.println("The queue is: " + q);
   }
}

Output

The queue is: [6, 1, 8, 4, 7]

class Queue:
   def __init__(self):
      self.queue = list()
   def __str__(self):
      return str(self.queue)
   def addtoqueue(self,data):
   
   # Insert method to add element
      if data not in self.queue:
         self.queue.insert(0,data)
         return True
      return False
   def peek(self):
      return self.queue[-1]

q = Queue()
q.addtoqueue("36")
q.addtoqueue("24")
q.addtoqueue("48")
q.addtoqueue("12")
q.addtoqueue("66")
print("Queue:")
print(q)
print("The frontmost element of the queue: ",q.peek())

Output

Queue:
['66', '12', '48', '24', '36']
The frontmost element of the queue:  36

The isFull() Operation

The isFull() operation verifies whether the stack is full.

Algorithm

1 – START
2 – If the count of queue elements equals the queue size, return true
3 – Otherwise, return false
4 – END

Example

Following are the implementations of this operation in various programming languages −

C C++ Java

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   int i;
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\n");
   if(isFull()) {
      printf("Queue is full!\n");
   }
}

Output

Queue: 3 5 9 1 12 15 
Queue is full!

#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   int i;
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\n");
   if(isFull()) {
      printf("Queue is full!\n");
   }
}

Output

Queue: 3 5 9 1 12 15 
Queue is full!

import java.io.*;
public class QueueExample {
   private int intArray[];
   private int front;
   private int rear;
   private int itemCount;
   private int MAX;
   QueueExample(int size) {
      intArray = new int[size];
      front = 0;
      rear = -1;
      MAX = size;
      itemCount = 0;
   }
   public boolean isFull() {
      return itemCount == MAX;
   }
   public void insert(int key) {
      if(!isFull()) {
         if(rear == MAX-1) {
            rear = -1;
         }
         intArray[++rear] = key;
         itemCount++;
      }
   }
   public static void main (String[] args) {
      QueueExample q = new QueueExample(5);
      q.insert(1); // inserting 1 in the stack
      q.insert(2);
      q.insert(3);
      q.insert(4);
      q.insert(5);
      System.out.println("Stack Full? " + q.isFull());
   }
}

Output

Stack Full? true

The isEmpty() operation

The isEmpty() operation verifies whether the stack is empty. This operation is used to check the status of the stack with the help of top pointer.

Algorithm

1 – START
2 – If the count of queue elements equals zero, return true
3 – Otherwise, return false
4 – END

Example

Following are the implementations of this operation in various programming languages −

C C++ Java

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isEmpty(){
   return itemCount == 0;
}
int main(){
   int i;
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\n");
   if(isEmpty()) {
      printf("Queue is Empty!\n");
   }
}

Output

Queue: 0 0 0 0 0 0 
Queue is Empty!

#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isEmpty(){
   return itemCount == 0;
}
int main(){
   int i;
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\n");
   if(isEmpty()) {
      printf("Queue is Empty!\n");
   }
}

Output

Queue: 0 0 0 0 0 0 
Queue is Empty!

import java.io.*;
public class QueueExample {
   private int intArray[];
   private int front;
   private int rear;
   private int itemCount;
   private int MAX;
   QueueExample(int size) {
      intArray = new int[size];
      front = 0;
      rear = -1;
      MAX = size;
      itemCount = 0;
   }
   public boolean isEmpty() {
      return itemCount == 0;
   }
   public static void main (String[] args) {
      QueueExample q = new QueueExample(5);
      System.out.println("Stack Empty? " + q.isEmpty());
   }
}

Output

Stack Empty? true

Implementation of Queue

In this chapter, the algorithm implementation of the Queue data structure is performed in four programming languages.

C C++ Java Python

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
   return intArray[front];
}
bool isEmpty(){
   return itemCount == 0;
}
bool isFull(){
   return itemCount == MAX;
}
int size(){
   return itemCount;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
int main(){
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);

   // front : 0
   // rear : 4
   // ------------------
   // index : 0 1 2 3 4
   // ------------------
   // queue : 3 5 9 1 12
   insert(15);

   // front : 0
   // rear : 5
   // ---------------------
   // index : 0 1 2 3 4 5
   // ---------------------
   // queue : 3 5 9 1 12 15
   if(isFull()) {
      printf("Queue is full!\n");
   }

   // remove one item
   int num = removeData();
   printf("Element removed: %d\n",num);

   // front : 1
   // rear : 5
   // -------------------
   // index : 1 2 3 4 5
   // -------------------
   // queue : 5 9 1 12 15
   // insert more items
   insert(16);
   
   // front : 1
   // rear : -1
   // ----------------------
   // index : 0 1 2 3 4 5
   // ----------------------
   // queue : 16 5 9 1 12 15
   // As queue is full, elements will not be inserted.
   insert(17);
   insert(18);

   // ----------------------
   // index : 0 1 2 3 4 5
   // ----------------------
   // queue : 16 5 9 1 12 15
   printf("Element at front: %d\n",peek());
   printf("----------------------\n");
   printf("index : 5 4 3 2 1 0\n");
   printf("----------------------\n");
   printf("Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      printf("%d ",n);
   }
}

Output

Queue is full!
Element removed: 3
Element at front: 5
----------------------
index : 5 4 3 2 1 0
----------------------
Queue: 5 9 1 12 15 16

#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
   return intArray[front];
}
bool isEmpty(){
   return itemCount == 0;
}
bool isFull(){
   return itemCount == MAX;
}
int size(){
   return itemCount;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
int main(){
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);

   // front : 0
   // rear : 4
   // ------------------
   // index : 0 1 2 3 4
   // ------------------
   // queue : 3 5 9 1 12
   insert(15);

   // front : 0
   // rear : 5
   // ---------------------
   // index : 0 1 2 3 4 5
   // ---------------------
   // queue : 3 5 9 1 12 15
   if(isFull()) {
      printf("Queue is full!\n");
   }

   // remove one item
   int num = removeData();
   printf("Element removed: %d\n",num);

   // front : 1
   // rear : 5
   // -------------------
   // index : 1 2 3 4 5
   // -------------------
   // queue : 5 9 1 12 15
   // insert more items
   insert(16);

   // front : 1
   // rear : -1
   // ----------------------
   // index : 0 1 2 3 4 5
   // ----------------------
   // queue : 16 5 9 1 12 15
   // As queue is full, elements will not be inserted.
   insert(17);
   insert(18);

   // ----------------------
   // index : 0 1 2 3 4 5
   // ----------------------
   // queue : 16 5 9 1 12 15
   printf("Element at front: %d\n",peek());
   printf("----------------------\n");
   printf("index : 5 4 3 2 1 0\n");
   printf("----------------------\n");
   printf("Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      printf("%d ",n);
   }
}

Output

Queue is full!
Element removed: 3
Element at front: 5
----------------------
index : 5 4 3 2 1 0
----------------------
Queue: 5 9 1 12 15 16

import java.util.LinkedList;
import java.util.Queue;
public class QueueExample {
   public static void main(String[] args) {
      Queue<Integer> q = new LinkedList<>();
      q.add(6);
      q.add(1);
      q.add(8);
      q.add(4);
      q.add(7);
      System.out.println("The queue is: " + q);
      int n = q.remove();
      System.out.println("The element deleted is: " + n);
      System.out.println("Queue after deletion: " + q);
      int size = q.size();
      System.out.println("Size of the queue is: " + size);
   }
}

Output

The queue is: [6, 1, 8, 4, 7]The element deleted is: 6
Queue after deletion: [1, 8, 4, 7]
Size of the queue is: 4

class Queue:
   def __init__(self):
      self.queue = list()
   def addtoqueue(self,data):

   # Insert method to add element
      if data not in self.queue:
         self.queue.insert(0,data)
         return True
      return False
   def size(self):
      return len(self.queue)
   def removefromqueue(self):
      if len(self.queue)>0:
         return self.queue.pop()
      return ("Queue is empty")

q = Queue()
q.addtoqueue("36")
q.addtoqueue("24")
q.addtoqueue("48")
q.addtoqueue("12")
q.addtoqueue("66")
print("size of the queue: ",q.size())
print("Element deleted from queue: ",q.removefromqueue())
print("size of the queue after deletion: ",q.size())

Output

size of the queue:  5
Element deleted from queue:  36
size of the queue after deletion:  4

Data Structure and Algorithms Linear Search

Linear search is a very simple search algorithm. In this type of search, a sequential search is made over all items one by one. Every item is checked and if a match is found then that particular item is returned, otherwise the search continues till the end of the data collection.

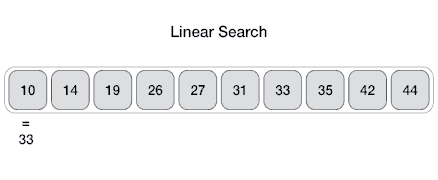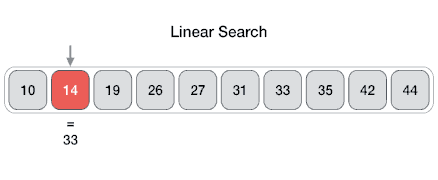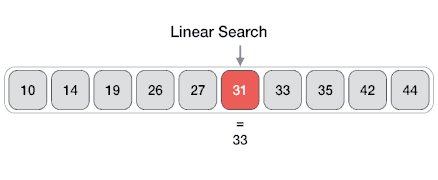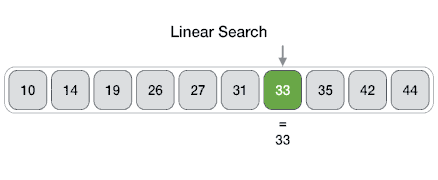
Algorithm

Linear Search ( Array A, Value x)

Step 1: Set i to 1
Step 2: if i > n then go to step 7
Step 3: if A[i] = x then go to step 6
Step 4: Set i to i + 1
Step 5: Go to Step 2
Step 6: Print Element x Found at index i and go to step 8
Step 7: Print element not found
Step 8: Exit

Pseudocode

procedure linear_search (list, value)

   for each item in the list
      if match item == value
         return the item's location
      end if
   end for

end procedure

To know about linear search implementation in C programming language, please click-here.

Data Structure and Algorithms Binary Search

Binary search is a fast search algorithm with run-time complexity of Ο(log n). This search algorithm works on the principle of divide and conquer. For this algorithm to work properly, the data collection should be in the sorted form.

Binary search looks for a particular item by comparing the middle most item of the collection. If a match occurs, then the index of item is returned. If the middle item is greater than the item, then the item is searched in the sub-array to the left of the middle item. Otherwise, the item is searched for in the sub-array to the right of the middle item. This process continues on the sub-array as well until the size of the subarray reduces to zero.

How Binary Search Works?

For a binary search to work, it is mandatory for the target array to be sorted. We shall learn the process of binary search with a pictorial example. The following is our sorted array and let us assume that we need to search the location of value 31 using binary search.

First, we shall determine half of the array by using this formula −

mid = low + (high - low) / 2

Here it is, 0 + (9 - 0 ) / 2 = 4 (integer value of 4.5). So, 4 is the mid of the array.

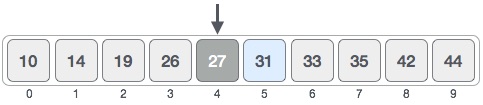
Now we compare the value stored at location 4, with the value being searched, i.e. 31. We find that the value at location 4 is 27, which is not a match. As the value is greater than 27 and we have a sorted array, so we also know that the target value must be in the upper portion of the array.

We change our low to mid + 1 and find the new mid value again.

low = mid + 1
mid = low + (high - low) / 2

Our new mid is 7 now. We compare the value stored at location 7 with our target value 31.

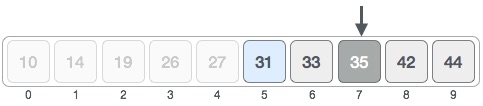
The value stored at location 7 is not a match, rather it is more than what we are looking for. So, the value must be in the lower part from this location.

Hence, we calculate the mid again. This time it is 5.

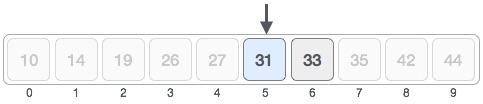
We compare the value stored at location 5 with our target value. We find that it is a match.

We conclude that the target value 31 is stored at location 5.

Binary search halves the searchable items and thus reduces the count of comparisons to be made to very less numbers.

Pseudocode

The pseudocode of binary search algorithms should look like this −

Procedure binary_search
   A ← sorted array
   n ← size of array
   x ← value to be searched

   Set lowerBound = 1
   Set upperBound = n 

   while x not found
      if upperBound < lowerBound 
         EXIT: x does not exists.
   
      set midPoint = lowerBound + ( upperBound - lowerBound ) / 2
      
      if A[midPoint] < x
         set lowerBound = midPoint + 1
         
      if A[midPoint] > x
         set upperBound = midPoint - 1 

      if A[midPoint] = x 
         EXIT: x found at location midPoint
   end while
   
end procedure

To know about binary search implementation using array in C programming language, please click here.

Data Structure - Interpolation Search

Interpolation search is an improved variant of binary search. This search algorithm works on the probing position of the required value. For this algorithm to work properly, the data collection should be in a sorted form and equally distributed.

Binary search has a huge advantage of time complexity over linear search. Linear search has worst-case complexity of Ο(n) whereas binary search has Ο(log n).

There are cases where the location of target data may be known in advance. For example, in case of a telephone directory, if we want to search the telephone number of Morphius. Here, linear search and even binary search will seem slow as we can directly jump to memory space where the names start from 'M' are stored.

Positioning in Binary Search

In binary search, if the desired data is not found then the rest of the list is divided in two parts, lower and higher. The search is carried out in either of them.

Even when the data is sorted, binary search does not take advantage to probe the position of the desired data.

Position Probing in Interpolation Search

Interpolation search finds a particular item by computing the probe position. Initially, the probe position is the position of the middle most item of the collection.

If a match occurs, then the index of the item is returned. To split the list into two parts, we use the following method −

mid = Lo + ((Hi - Lo) / (A[Hi] - A[Lo])) * (X - A[Lo])

Where −
   A    = list
   Lo   = Lowest index of the list
   Hi   = Highest index of the list
   A[n] = Value stored at index n in the list

If the middle item is greater than the item, then the probe position is again calculated in the sub-array to the right of the middle item. Otherwise, the item is searched in the subarray to the left of the middle item. This process continues on the sub-array as well until the size of subarray reduces to zero.

Runtime complexity of interpolation search algorithm is Ο(log (log n)) as compared to Ο(log n) of BST in favorable situations.

Algorithm

As it is an improvisation of the existing BST algorithm, we are mentioning the steps to search the 'target' data value index, using position probing −

Step 1 − Start searching data from middle of the list.
Step 2 − If it is a match, return the index of the item, and exit.
Step 3 − If it is not a match, probe position.
Step 4 − Divide the list using probing formula and find the new midle.
Step 5 − If data is greater than middle, search in higher sub-list.
Step 6 − If data is smaller than middle, search in lower sub-list.
Step 7 − Repeat until match.

Pseudocode

A → Array list
N → Size of A
X → Target Value

Procedure Interpolation_Search()

   Set Lo  →  0
   Set Mid → -1
   Set Hi  →  N-1

   While X does not match
   
      if Lo equals to Hi OR A[Lo] equals to A[Hi]
         EXIT: Failure, Target not found
      end if
      
      Set Mid = Lo + ((Hi - Lo) / (A[Hi] - A[Lo])) * (X - A[Lo]) 

      if A[Mid] = X
         EXIT: Success, Target found at Mid
      else 
         if A[Mid] < X
            Set Lo to Mid+1
         else if A[Mid] > X
            Set Hi to Mid-1
         end if
      end if
   End While

End Procedure

To know about the implementation of interpolation search in C programming language, click here.

Data Structure and Algorithms - Hash Table

Hash Table is a data structure which stores data in an associative manner. In a hash table, data is stored in an array format, where each data value has its own unique index value. Access of data becomes very fast if we know the index of the desired data.

Thus, it becomes a data structure in which insertion and search operations are very fast irrespective of the size of the data. Hash Table uses an array as a storage medium and uses hash technique to generate an index where an element is to be inserted or is to be located from.

Hashing

Hashing is a technique to convert a range of key values into a range of indexes of an array. We're going to use modulo operator to get a range of key values. Consider an example of hash table of size 20, and the following items are to be stored. Item are in the (key,value) format.

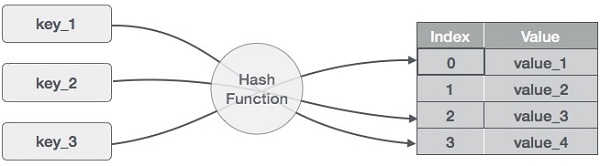
(1,20)
(2,70)
(42,80)
(4,25)
(12,44)
(14,32)
(17,11)
(13,78)
(37,98)

Sr.No.	Key	Hash	Array Index
1	1	1 % 20 = 1	1
2	2	2 % 20 = 2	2
3	42	42 % 20 = 2	2
4	4	4 % 20 = 4	4
5	12	12 % 20 = 12	12
6	14	14 % 20 = 14	14
7	17	17 % 20 = 17	17
8	13	13 % 20 = 13	13
9	37	37 % 20 = 17	17

Linear Probing

As we can see, it may happen that the hashing technique is used to create an already used index of the array. In such a case, we can search the next empty location in the array by looking into the next cell until we find an empty cell. This technique is called linear probing.

Sr.No.	Key	Hash	Array Index	After Linear Probing, Array Index
1	1	1 % 20 = 1	1	1
2	2	2 % 20 = 2	2	2
3	42	42 % 20 = 2	2	3
4	4	4 % 20 = 4	4	4
5	12	12 % 20 = 12	12	12
6	14	14 % 20 = 14	14	14
7	17	17 % 20 = 17	17	17
8	13	13 % 20 = 13	13	13
9	37	37 % 20 = 17	17	18

Basic Operations

Following are the basic primary operations of a hash table.

Search − Searches an element in a hash table.
Insert − inserts an element in a hash table.
delete − Deletes an element from a hash table.

DataItem

Define a data item having some data and key, based on which the search is to be conducted in a hash table.

struct DataItem {
   int data;
   int key;
};

Hash Method

Define a hashing method to compute the hash code of the key of the data item.

int hashCode(int key){
   return key % SIZE;
}

Search Operation

Whenever an element is to be searched, compute the hash code of the key passed and locate the element using that hash code as index in the array. Use linear probing to get the element ahead if the element is not found at the computed hash code.

Example

struct DataItem *search(int key) {
   //get the hash
   int hashIndex = hashCode(key);
	
   //move in array until an empty
   while(hashArray[hashIndex] != NULL) {
	
      if(hashArray[hashIndex]->key == key)
         return hashArray[hashIndex];
			
      //go to next cell
      ++hashIndex;
		
      //wrap around the table
      hashIndex %= SIZE;
   }

   return NULL;        
}

Insert Operation

Whenever an element is to be inserted, compute the hash code of the key passed and locate the index using that hash code as an index in the array. Use linear probing for empty location, if an element is found at the computed hash code.

Example

void insert(int key,int data) {
   struct DataItem *item = (struct DataItem*) malloc(sizeof(struct DataItem));
   item->data = data;  
   item->key = key;     

   //get the hash 
   int hashIndex = hashCode(key);

   //move in array until an empty or deleted cell
   while(hashArray[hashIndex] != NULL && hashArray[hashIndex]->key != -1) {
      //go to next cell
      ++hashIndex;
		
      //wrap around the table
      hashIndex %= SIZE;
   }
	
   hashArray[hashIndex] = item;        
}

Delete Operation

Whenever an element is to be deleted, compute the hash code of the key passed and locate the index using that hash code as an index in the array. Use linear probing to get the element ahead if an element is not found at the computed hash code. When found, store a dummy item there to keep the performance of the hash table intact.

Example

struct DataItem* delete(struct DataItem* item) {
   int key = item->key;

   //get the hash 
   int hashIndex = hashCode(key);

   //move in array until an empty 
   while(hashArray[hashIndex] !=NULL) {
	
      if(hashArray[hashIndex]->key == key) {
         struct DataItem* temp = hashArray[hashIndex]; 
			
         //assign a dummy item at deleted position
         hashArray[hashIndex] = dummyItem; 
         return temp;
      } 
		
      //go to next cell
      ++hashIndex;
		
      //wrap around the table
      hashIndex %= SIZE;
   }  
	
   return NULL;        
}

To know about hash implementation in C programming language, please click here.

Data Structure - Sorting Techniques

Sorting refers to arranging data in a particular format. Sorting algorithm specifies the way to arrange data in a particular order. Most common orders are in numerical or lexicographical order.

The importance of sorting lies in the fact that data searching can be optimized to a very high level, if data is stored in a sorted manner. Sorting is also used to represent data in more readable formats. Following are some of the examples of sorting in real-life scenarios −

Telephone Directory − The telephone directory stores the telephone numbers of people sorted by their names, so that the names can be searched easily.
Dictionary − The dictionary stores words in an alphabetical order so that searching of any word becomes easy.

In-place Sorting and Not-in-place Sorting

Sorting algorithms may require some extra space for comparison and temporary storage of few data elements. These algorithms do not require any extra space and sorting is said to happen in-place, or for example, within the array itself. This is called in-place sorting. Bubble sort is an example of in-place sorting.

However, in some sorting algorithms, the program requires space which is more than or equal to the elements being sorted. Sorting which uses equal or more space is called not-in-place sorting. Merge-sort is an example of not-in-place sorting.

Stable and Not Stable Sorting

If a sorting algorithm, after sorting the contents, does not change the sequence of similar content in which they appear, it is called stable sorting.

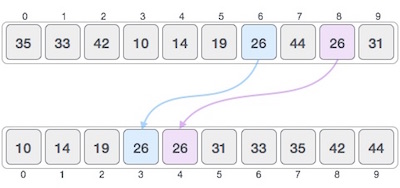
If a sorting algorithm, after sorting the contents, changes the sequence of similar content in which they appear, it is called unstable sorting.

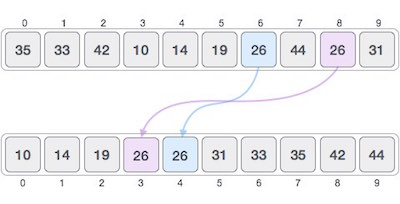
Stability of an algorithm matters when we wish to maintain the sequence of original elements, like in a tuple for example.

Adaptive and Non-Adaptive Sorting Algorithm

A sorting algorithm is said to be adaptive, if it takes advantage of already 'sorted' elements in the list that is to be sorted. That is, while sorting if the source list has some element already sorted, adaptive algorithms will take this into account and will try not to re-order them.

A non-adaptive algorithm is one which does not take into account the elements which are already sorted. They try to force every single element to be re-ordered to confirm their sortedness.

Important Terms

Some terms are generally coined while discussing sorting techniques, here is a brief introduction to them −

Increasing Order

A sequence of values is said to be in increasing order, if the successive element is greater than the previous one. For example, 1, 3, 4, 6, 8, 9 are in increasing order, as every next element is greater than the previous element.

Decreasing Order

A sequence of values is said to be in decreasing order, if the successive element is less than the current one. For example, 9, 8, 6, 4, 3, 1 are in decreasing order, as every next element is less than the previous element.

Non-Increasing Order

A sequence of values is said to be in non-increasing order, if the successive element is less than or equal to its previous element in the sequence. This order occurs when the sequence contains duplicate values. For example, 9, 8, 6, 3, 3, 1 are in non-increasing order, as every next element is less than or equal to (in case of 3) but not greater than any previous element.

Non-Decreasing Order

A sequence of values is said to be in non-decreasing order, if the successive element is greater than or equal to its previous element in the sequence. This order occurs when the sequence contains duplicate values. For example, 1, 3, 3, 6, 8, 9 are in non-decreasing order, as every next element is greater than or equal to (in case of 3) but not less than the previous one.

Data Structure - Bubble Sort Algorithm

Bubble sort is a simple sorting algorithm. This sorting algorithm is comparison-based algorithm in which each pair of adjacent elements is compared and the elements are swapped if they are not in order. This algorithm is not suitable for large data sets as its average and worst case complexity are of Ο(n²) where n is the number of items.

How Bubble Sort Works?

We take an unsorted array for our example. Bubble sort takes Ο(n²) time so we're keeping it short and precise.

Bubble sort starts with very first two elements, comparing them to check which one is greater.

In this case, value 33 is greater than 14, so it is already in sorted locations. Next, we compare 33 with 27.

We find that 27 is smaller than 33 and these two values must be swapped.

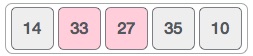
The new array should look like this −

Next we compare 33 and 35. We find that both are in already sorted positions.

Then we move to the next two values, 35 and 10.

We know then that 10 is smaller 35. Hence they are not sorted.

We swap these values. We find that we have reached the end of the array. After one iteration, the array should look like this −

To be precise, we are now showing how an array should look like after each iteration. After the second iteration, it should look like this −

Notice that after each iteration, at least one value moves at the end.

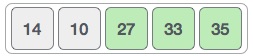
And when there's no swap required, bubble sorts learns that an array is completely sorted.

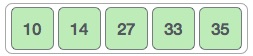
Now we should look into some practical aspects of bubble sort.

Algorithm

We assume list is an array of n elements. We further assume that swap function swaps the values of the given array elements.

begin BubbleSort(list)

   for all elements of list
      if list[i] > list[i+1]
         swap(list[i], list[i+1])
      end if
   end for
   
   return list
   
end BubbleSort

Pseudocode

We observe in algorithm that Bubble Sort compares each pair of array element unless the whole array is completely sorted in an ascending order. This may cause a few complexity issues like what if the array needs no more swapping as all the elements are already ascending.

To ease-out the issue, we use one flag variable swapped which will help us see if any swap has happened or not. If no swap has occurred, i.e. the array requires no more processing to be sorted, it will come out of the loop.

Pseudocode of BubbleSort algorithm can be written as follows −

procedure bubbleSort( list : array of items )

   loop = list.count;
   
   for i = 0 to loop-1 do:
      swapped = false
		
      for j = 0 to loop-1 do:
      
         /* compare the adjacent elements */   
         if list[j] > list[j+1] then
            /* swap them */
            swap( list[j], list[j+1] )		 
            swapped = true
         end if
         
      end for
      
      /*if no number was swapped that means 
      array is sorted now, break the loop.*/
      
      if(not swapped) then
         break
      end if
      
   end for
   
end procedure return list

Implementation

One more issue we did not address in our original algorithm and its improvised pseudocode, is that, after every iteration the highest values settles down at the end of the array. Hence, the next iteration need not include already sorted elements. For this purpose, in our implementation, we restrict the inner loop to avoid already sorted values.

To know about bubble sort implementation in C programming language, please click here.

Data Structure and Algorithms Insertion Sort

This is an in-place comparison-based sorting algorithm. Here, a sub-list is maintained which is always sorted. For example, the lower part of an array is maintained to be sorted. An element which is to be 'insert'ed in this sorted sub-list, has to find its appropriate place and then it has to be inserted there. Hence the name, insertion sort.

The array is searched sequentially and unsorted items are moved and inserted into the sorted sub-list (in the same array). This algorithm is not suitable for large data sets as its average and worst case complexity are of Ο(n²), where n is the number of items.

How Insertion Sort Works?

We take an unsorted array for our example.

Insertion sort compares the first two elements.

It finds that both 14 and 33 are already in ascending order. For now, 14 is in sorted sub-list.

Insertion sort moves ahead and compares 33 with 27.

And finds that 33 is not in the correct position.

It swaps 33 with 27. It also checks with all the elements of sorted sub-list. Here we see that the sorted sub-list has only one element 14, and 27 is greater than 14. Hence, the sorted sub-list remains sorted after swapping.

By now we have 14 and 27 in the sorted sub-list. Next, it compares 33 with 10.

These values are not in a sorted order.

So we swap them.

However, swapping makes 27 and 10 unsorted.

Hence, we swap them too.

Again we find 14 and 10 in an unsorted order.

We swap them again. By the end of third iteration, we have a sorted sub-list of 4 items.

This process goes on until all the unsorted values are covered in a sorted sub-list. Now we shall see some programming aspects of insertion sort.

Algorithm

Now we have a bigger picture of how this sorting technique works, so we can derive simple steps by which we can achieve insertion sort.

Step 1 − If it is the first element, it is already sorted. return 1;
Step 2 − Pick next element
Step 3 − Compare with all elements in the sorted sub-list
Step 4 − Shift all the elements in the sorted sub-list that is greater than the 
         value to be sorted
Step 5 − Insert the value
Step 6 − Repeat until list is sorted

Pseudocode

procedure insertionSort( A : array of items )
   int holePosition
   int valueToInsert
	
   for i = 1 to length(A) inclusive do:
	
      /* select value to be inserted */
      valueToInsert = A[i]
      holePosition = i
      
      /*locate hole position for the element to be inserted */
		
      while holePosition > 0 and A[holePosition-1] > valueToInsert do:
         A[holePosition] = A[holePosition-1]
         holePosition = holePosition -1
      end while
		
      /* insert the number at hole position */
      A[holePosition] = valueToInsert
      
   end for
	
end procedure

To know about insertion sort implementation in C programming language, please click here.

Data Structure and Algorithms Selection Sort

Selection sort is a simple sorting algorithm. This sorting algorithm is an in-place comparison-based algorithm in which the list is divided into two parts, the sorted part at the left end and the unsorted part at the right end. Initially, the sorted part is empty and the unsorted part is the entire list.

The smallest element is selected from the unsorted array and swapped with the leftmost element, and that element becomes a part of the sorted array. This process continues moving unsorted array boundary by one element to the right.

This algorithm is not suitable for large data sets as its average and worst case complexities are of Ο(n²), where n is the number of items.

How Selection Sort Works?

Consider the following depicted array as an example.

For the first position in the sorted list, the whole list is scanned sequentially. The first position where 14 is stored presently, we search the whole list and find that 10 is the lowest value.

So we replace 14 with 10. After one iteration 10, which happens to be the minimum value in the list, appears in the first position of the sorted list.

For the second position, where 33 is residing, we start scanning the rest of the list in a linear manner.

We find that 14 is the second lowest value in the list and it should appear at the second place. We swap these values.

After two iterations, two least values are positioned at the beginning in a sorted manner.

The same process is applied to the rest of the items in the array.

Following is a pictorial depiction of the entire sorting process −

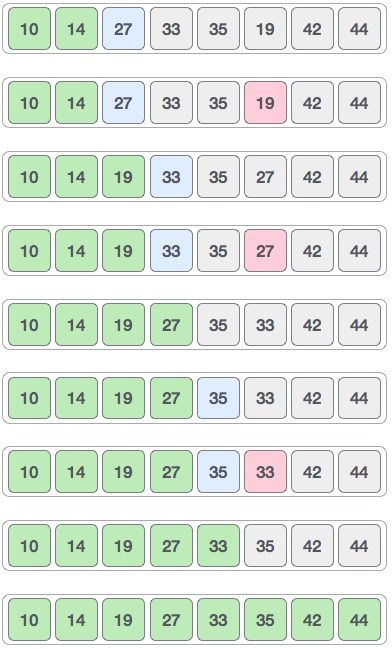
Now, let us learn some programming aspects of selection sort.

Algorithm

Step 1 − Set MIN to location 0
Step 2 − Search the minimum element in the list
Step 3 − Swap with value at location MIN
Step 4 − Increment MIN to point to next element
Step 5 − Repeat until list is sorted

Pseudocode

procedure selection sort 
   list  : array of items
   n     : size of list

   for i = 1 to n - 1
   /* set current element as minimum*/
      min = i    
  
      /* check the element to be minimum */

      for j = i+1 to n 
         if list[j] < list[min] then
            min = j;
         end if
      end for

      /* swap the minimum element with the current element*/
      if indexMin != i  then
         swap list[min] and list[i]
      end if
   end for
	
end procedure

To know about selection sort implementation in C programming language, please click here.

Data Structures - Merge Sort Algorithm

Merge sort is a sorting technique based on divide and conquer technique. With worst-case time complexity being Ο(n log n), it is one of the most respected algorithms.

Merge sort first divides the array into equal halves and then combines them in a sorted manner.

How Merge Sort Works?

To understand merge sort, we take an unsorted array as the following −

We know that merge sort first divides the whole array iteratively into equal halves unless the atomic values are achieved. We see here that an array of 8 items is divided into two arrays of size 4.

This does not change the sequence of appearance of items in the original. Now we divide these two arrays into halves.

We further divide these arrays and we achieve atomic value which can no more be divided.

Now, we combine them in exactly the same manner as they were broken down. Please note the color codes given to these lists.

We first compare the element for each list and then combine them into another list in a sorted manner. We see that 14 and 33 are in sorted positions. We compare 27 and 10 and in the target list of 2 values we put 10 first, followed by 27. We change the order of 19 and 35 whereas 42 and 44 are placed sequentially.

In the next iteration of the combining phase, we compare lists of two data values, and merge them into a list of found data values placing all in a sorted order.

After the final merging, the list should look like this −

Now we should learn some programming aspects of merge sorting.

Algorithm

Merge sort keeps on dividing the list into equal halves until it can no more be divided. By definition, if it is only one element in the list, it is sorted. Then, merge sort combines the smaller sorted lists keeping the new list sorted too.

Step 1 − if it is only one element in the list it is already sorted, return.
Step 2 − divide the list recursively into two halves until it can no more be divided.
Step 3 − merge the smaller lists into new list in sorted order.

Pseudocode

We shall now see the pseudocodes for merge sort functions. As our algorithms point out two main functions − divide & merge.

Merge sort works with recursion and we shall see our implementation in the same way.

procedure mergesort( var a as array )
   if ( n == 1 ) return a

   var l1 as array = a[0] ... a[n/2]
   var l2 as array = a[n/2+1] ... a[n]

   l1 = mergesort( l1 )
   l2 = mergesort( l2 )

   return merge( l1, l2 )
end procedure

procedure merge( var a as array, var b as array )

   var c as array
   while ( a and b have elements )
      if ( a[0] > b[0] )
         add b[0] to the end of c
         remove b[0] from b
      else
         add a[0] to the end of c
         remove a[0] from a
      end if
   end while
   
   while ( a has elements )
      add a[0] to the end of c
      remove a[0] from a
   end while
   
   while ( b has elements )
      add b[0] to the end of c
      remove b[0] from b
   end while
   
   return c
	
end procedure

To know about merge sort implementation in C programming language, please click here.

Data Structure and Algorithms - Shell Sort

Shell sort is a highly efficient sorting algorithm and is based on insertion sort algorithm. This algorithm avoids large shifts as in case of insertion sort, if the smaller value is to the far right and has to be moved to the far left.

This algorithm uses insertion sort on a widely spread elements, first to sort them and then sorts the less widely spaced elements. This spacing is termed as interval. This interval is calculated based on Knuth's formula as −

Knuth's Formula

h = h * 3 + 1
where −
   h is interval with initial value 1

This algorithm is quite efficient for medium-sized data sets as its average and worst-case complexity of this algorithm depends on the gap sequence the best known is Ο(n), where n is the number of items. And the worst case space complexity is O(n).

How Shell Sort Works?

Let us consider the following example to have an idea of how shell sort works. We take the same array we have used in our previous examples. For our example and ease of understanding, we take the interval of 4. Make a virtual sub-list of all values located at the interval of 4 positions. Here these values are {35, 14}, {33, 19}, {42, 27} and {10, 44}

We compare values in each sub-list and swap them (if necessary) in the original array. After this step, the new array should look like this −

Then, we take interval of 1 and this gap generates two sub-lists - {14, 27, 35, 42}, {19, 10, 33, 44}

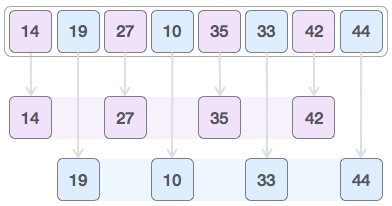
We compare and swap the values, if required, in the original array. After this step, the array should look like this −

Finally, we sort the rest of the array using interval of value 1. Shell sort uses insertion sort to sort the array.

Following is the step-by-step depiction −

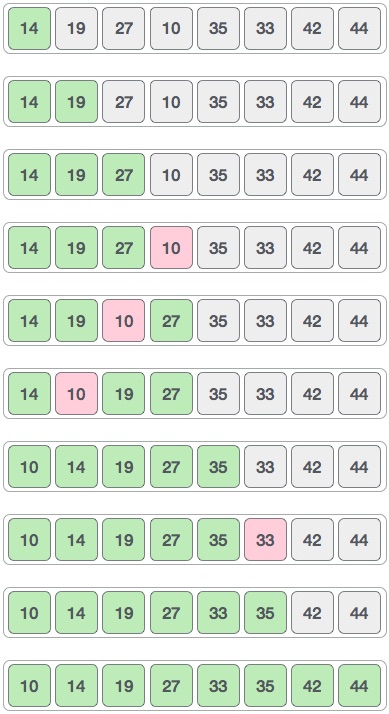
We see that it required only four swaps to sort the rest of the array.

Algorithm

Following is the algorithm for shell sort.

Step 1 − Initialize the value of h
Step 2 − Divide the list into smaller sub-list of equal interval h
Step 3 − Sort these sub-lists using insertion sort
Step 3 − Repeat until complete list is sorted

Pseudocode

Following is the pseudocode for shell sort.

procedure shellSort()
   A : array of items 
	
   /* calculate interval*/
   while interval < A.length /3 do:
      interval = interval * 3 + 1	    
   end while
   
   while interval > 0 do:

      for outer = interval; outer < A.length; outer ++ do:

      /* select value to be inserted */
      valueToInsert = A[outer]
      inner = outer;

         /*shift element towards right*/
         while inner > interval -1 && A[inner - interval] >= valueToInsert do:
            A[inner] = A[inner - interval]
            inner = inner - interval
         end while

      /* insert the number at hole position */
      A[inner] = valueToInsert

      end for

   /* calculate interval*/
   interval = (interval -1) /3;	  

   end while
   
end procedure

To know about shell sort implementation in C programming language, please click here.

Data Structure and Algorithms - Quick Sort

Quick sort is a highly efficient sorting algorithm and is based on partitioning of array of data into smaller arrays. A large array is partitioned into two arrays one of which holds values smaller than the specified value, say pivot, based on which the partition is made and another array holds values greater than the pivot value.

Quicksort partitions an array and then calls itself recursively twice to sort the two resulting subarrays. This algorithm is quite efficient for large-sized data sets as its average and worst-case complexity are O(n²), respectively.

Partition in Quick Sort

Following animated representation explains how to find the pivot value in an array.

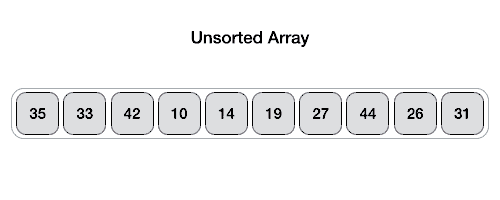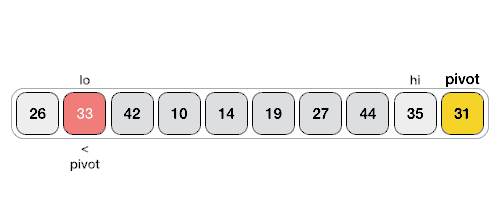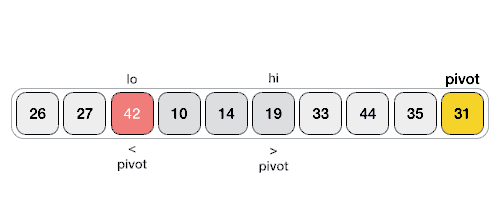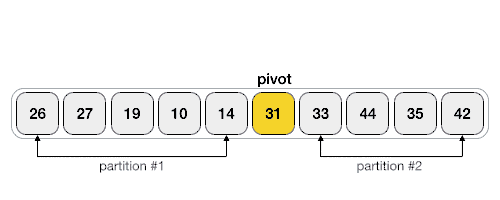
The pivot value divides the list into two parts. And recursively, we find the pivot for each sub-lists until all lists contains only one element.

Quick Sort Pivot Algorithm

Based on our understanding of partitioning in quick sort, we will now try to write an algorithm for it, which is as follows.

Step 1 − Choose the highest index value has pivot
Step 2 − Take two variables to point left and right of the list excluding pivot
Step 3 − left points to the low index
Step 4 − right points to the high
Step 5 − while value at left is less than pivot move right
Step 6 − while value at right is greater than pivot move left
Step 7 − if both step 5 and step 6 does not match swap left and right
Step 8 − if left ≥ right, the point where they met is new pivot

Quick Sort Pivot Pseudocode

The pseudocode for the above algorithm can be derived as −

function partitionFunc(left, right, pivot)
   leftPointer = left
   rightPointer = right - 1

   while True do
      while A[++leftPointer] < pivot do
         //do-nothing            
      end while
		
      while rightPointer > 0 && A[--rightPointer] > pivot do
         //do-nothing         
      end while
		
      if leftPointer >= rightPointer
         break
      else                
         swap leftPointer,rightPointer
      end if
		
   end while 
	
   swap leftPointer,right
   return leftPointer
	
end function

Quick Sort Algorithm

Using pivot algorithm recursively, we end up with smaller possible partitions. Each partition is then processed for quick sort. We define recursive algorithm for quicksort as follows −

Step 1 − Make the right-most index value pivot
Step 2 − partition the array using pivot value
Step 3 − quicksort left partition recursively
Step 4 − quicksort right partition recursively

Quick Sort Pseudocode

To get more into it, let see the pseudocode for quick sort algorithm −

procedure quickSort(left, right)

   if right-left <= 0
      return
   else     
      pivot = A[right]
      partition = partitionFunc(left, right, pivot)
      quickSort(left,partition-1)
      quickSort(partition+1,right)    
   end if		
   
end procedure

To know about quick sort implementation in C programming language, please click here.

Data Structure - Graph Data Structure

A graph is an abstract data type (ADT) that consists of a set of objects that are connected to each other via links. These objects are called vertices and the links are called edges.

Usually, a graph is represented as G = {V, E}, where G is the graph space, V is the set of vertices and E is the set of edges. If E is empty, the graph is known as a forest.

Before we proceed further, let's familiarize ourselves with some important terms −

Vertex − Each node of the graph is represented as a vertex. In the following example, the labelled circle represents vertices. Thus, A to G are vertices. We can represent them using an array as shown in the following image. Here A can be identified by index 0. B can be identified using index 1 and so on.
Edge − Edge represents a path between two vertices or a line between two vertices. In the following example, the lines from A to B, B to C, and so on represents edges. We can use a two-dimensional array to represent an array as shown in the following image. Here AB can be represented as 1 at row 0, column 1, BC as 1 at row 1, column 2 and so on, keeping other combinations as 0.
Adjacency − Two node or vertices are adjacent if they are connected to each other through an edge. In the following example, B is adjacent to A, C is adjacent to B, and so on.
Path − Path represents a sequence of edges between the two vertices. In the following example, ABCD represents a path from A to D.

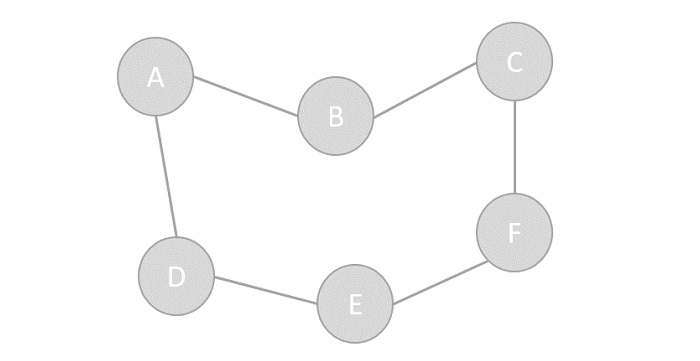
Operations of Graphs

The primary operations of a graph include creating a graph with vertices and edges, and displaying the said graph. However, one of the most common and popular operation performed using graphs are Traversal, i.e. visiting every vertex of the graph in a specific order.

There are two types of traversals in Graphs −

Depth First Search Traversal
Breadth First Search Traversal

Depth First Search Traversal

Depth First Search is a traversal algorithm that visits all the vertices of a graph in the decreasing order of its depth. In this algorithm, an arbitrary node is chosen as the starting point and the graph is traversed back and forth by marking unvisited adjacent nodes until all the vertices are marked.

The DFS traversal uses the stack data structure to keep track of the unvisited nodes.

Breadth First Search Traversal

Breadth First Search is a traversal algorithm that visits all the vertices of a graph present at one level of the depth before moving to the next level of depth. In this algorithm, an arbitrary node is chosen as the starting point and the graph is traversed by visiting the adjacent vertices on the same depth level and marking them until there is no vertex left.

The DFS traversal uses the queue data structure to keep track of the unvisited nodes.

Representation of Graphs

While representing graphs, we must carefully depict the elements (vertices and edges) present in the graph and the relationship between them. Pictorially, a graph is represented with a finite set of nodes and connecting links between them. However, we can also represent the graph in other most commonly used ways, like −

Adjacency Matrix
Adjacency List

Adjacency Matrix

The Adjacency Matrix is a V×V matrix where the values are filled with either 0 or 1. If the link exists between Vi and Vj, it is recorded 1; otherwise, 0.

For the given graph below, let us construct an adjacency matrix −

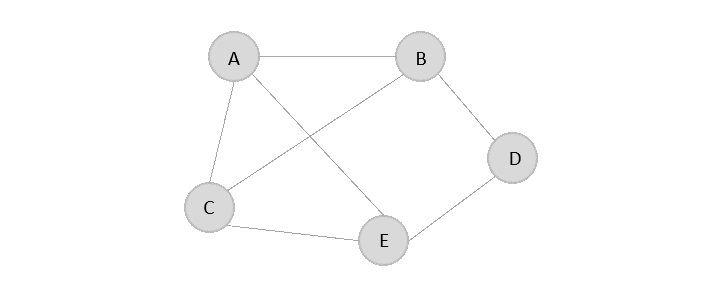
The adjacency matrix is −

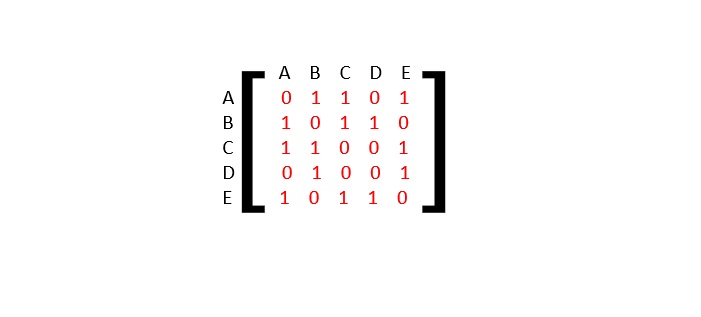
Adjacency List

The adjacency list is a list of the vertices directly connected to the other vertices in the graph.

The adjacency list is −

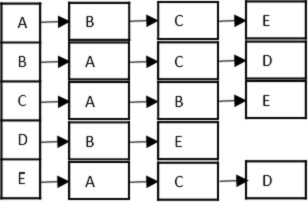
Types of graph

There are two basic types of graph −

Directed Graph
Undirected Graph

Directed graph, as the name suggests, consists of edges that possess a direction that goes either away from a vertex or towards the vertex. Undirected graphs have edges that are not directed at all.

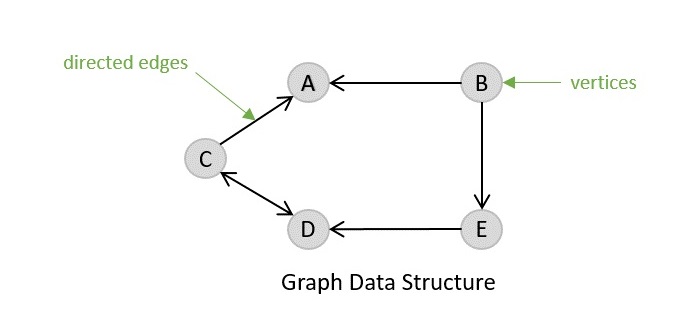
Directed Graph

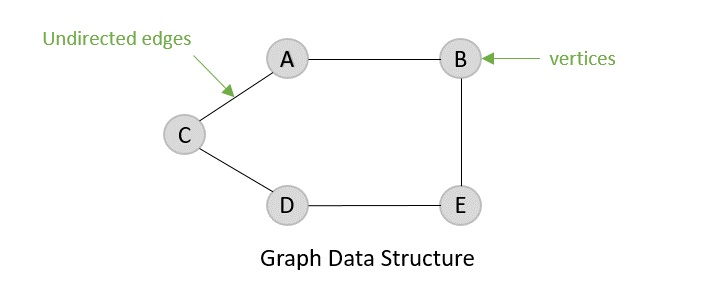
Undirected Graph

Spanning Tree

A spanning tree is a subset of an undirected graph that contains all the vertices of the graph connected with the minimum number of edges in the graph. Precisely, the edges of the spanning tree is a subset of the edges in the original graph.

If all the vertices are connected in a graph, then there exists at least one spanning tree. In a graph, there may exist more than one spanning tree.

Properties

A spanning tree does not have any cycle.
Any vertex can be reached from any other vertex.

Example

In the following graph, the highlighted edges form a spanning tree.

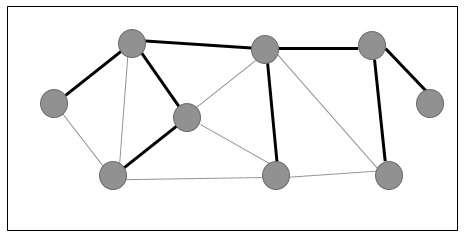
Minimum Spanning Tree

A Minimum Spanning Tree (MST) is a subset of edges of a connected weighted undirected graph that connects all the vertices together with the minimum possible total edge weight. To derive an MST, Prim’s algorithm or Kruskal’s algorithm can be used. Hence, we will discuss Prim’s algorithm in this chapter.

As we have discussed, one graph may have more than one spanning tree. If there are n number of vertices, the spanning tree should have 𝒏−𝟏 number of edges. In this context, if each edge of the graph is associated with a weight and there exists more than one spanning tree, we need to find the minimum spanning tree of the graph.

Moreover, if there exist any duplicate weighted edges, the graph may have multiple minimum spanning tree.

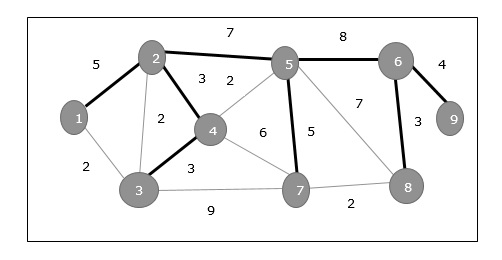
In the above graph, we have shown a spanning tree though it’s not the minimum spanning tree. The cost of this spanning tree is (5+7+3+3+5+8+3+4)=38.

Shortest Path

The shortest path in a graph is defined as the minimum cost route from one vertex to another. This is most commonly seen in weighted directed graphs but are also applicable to undirected graphs.

A popular real-world application of finding the shortest path in a graph is a map. Navigation is made easier and simpler with the various shortest path algorithms where destinations are considered vertices of the graph and routes are the edges. The two common shortest path algorithms are −

Dijkstra’s Shortest Path Algorithm
Bellman Ford’s Shortest Path Algorithm

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
#include<stdlib.h>
#include <stdlib.h>
#define V 5 

// Maximum number of vertices in the graph
struct graph { 
   
   // declaring graph data structure
   struct vertex *point[V];
};
struct vertex { 
   
   // declaring vertices
   int end;
   struct vertex *next;
};
struct Edge { 
   
   // declaring edges
   int end, start;
};
struct graph *create_graph (struct Edge edges[], int x){
   int i;
   struct graph *graph = (struct graph *) malloc (sizeof (struct graph));
   for (i = 0; i < V; i++) {
      graph->point[i] = NULL;
   }
   for (i = 0; i < x; i++) {
      int start = edges[i].start;
      int end = edges[i].end;
      struct vertex *v = (struct vertex *) malloc (sizeof (struct vertex));
      v->end = end;
      v->next = graph->point[start];
      graph->point[start] = v;
   }
   return graph;
}
int main (){
   struct Edge edges[] = { {0, 1}, {0, 2}, {0, 3}, {1, 2}, {1, 4}, {2, 4}, {2, 3}, {3, 1} };
   int n = sizeof (edges) / sizeof (edges[0]);
   struct graph *graph = create_graph (edges, n);
   int i;
   for (i = 0; i < V; i++) {
      struct vertex *ptr = graph->point[i];
      while (ptr != NULL) {
         printf ("(%d -> %d)\t", i, ptr->end);
         ptr = ptr->next;
      }
      printf ("\n");
   }
   return 0;
}

Output

(1 -> 3)	(1 -> 0)	
(2 -> 1)	(2 -> 0)	
(3 -> 2)	(3 -> 0)	
(4 -> 2)	(4 -> 1)

#include <bits/stdc++.h>
using namespace std;
#define V 5 

// Maximum number of vertices in the graph
struct graph { 
   
   // declaring graph data structure
   struct vertex *point[V];
};
struct vertex { 
   
   // declaring vertices
   int end;
   struct vertex *next;
};
struct Edge { 
   
   // declaring edges
   int end, start;
};
struct graph *create_graph (struct Edge edges[], int x){
   int i;
   struct graph *graph = (struct graph *) malloc (sizeof (struct graph));
   for (i = 0; i < V; i++) {
      graph->point[i] = NULL;
   }
   for (i = 0; i < x; i++) {
      int start = edges[i].start;
      int end = edges[i].end;
      struct vertex *v = (struct vertex *) malloc (sizeof (struct vertex));
      v->end = end;
      v->next = graph->point[start];
      graph->point[start] = v;
   }
   return graph;
}
int main (){
   struct Edge edges[] = { {0, 1}, {0, 2}, {0, 3}, {1, 2}, {1, 4}, {2, 4}, {2, 3}, {3, 1} };
   int n = sizeof (edges) / sizeof (edges[0]);
   struct graph *graph = create_graph (edges, n);
   int i;
   for (i = 0; i < V; i++) {
      struct vertex *ptr = graph->point[i];
      while (ptr != NULL) {
         cout << "(" << i << " -> " << ptr->end << ")\t";
         ptr = ptr->next;
      }
      cout << endl;
   }
   return 0;
}

Output

(1 -> 3)	(1 -> 0)	
(2 -> 1)	(2 -> 0)	
(3 -> 2)	(3 -> 0)	
(4 -> 2)	(4 -> 1)

import java.util.*;

//class to store edges of the graph
class Edge {   
   int src, dest;
   Edge(int src, int dest) {
      this.src = src;
      this.dest = dest;
   }
}

// Graph class
public class Graph {
   
   // node of adjacency list
   static class vertex {
      int v;
      vertex(int v) {
        this.v = v;
      }
   };
   // define adjacency list to represent the graph
   List<List<vertex>> adj_list = new ArrayList<>();
   
   //Graph Constructor
   public Graph(List<Edge> edges){
      
      // adjacency list memory allocation
      for (int i = 0; i < edges.size(); i++)
      adj_list.add(i, new ArrayList<>());
      
      // add edges to the graph
      for (Edge e : edges){
        
        // allocate new node in adjacency List from src to dest
        adj_list.get(e.src).add(new vertex(e.dest));
      }
   }
   public static void main (String[] args) {
      
      // define edges of the graph
      List<Edge> edges = Arrays.asList(new Edge(0, 1),new Edge(0, 2),
      new Edge(0, 3),new Edge(1, 2), new Edge(1, 4),
      new Edge(2, 4), new Edge(2, 3),new Edge(3, 1));
      
      // call graph class Constructor to construct a graph
      Graph graph = new Graph(edges);
      
      // print the graph as an adjacency list
      int src = 0;
      int lsize = graph.adj_list.size();
      System.out.println("The graph created is:");
      while (src < lsize) {
      
         //traverse through the adjacency list and print the edges
         for (vertex edge : graph.adj_list.get(src)) {
            System.out.print(src + " -> " + edge.v + "\t");
         }
         System.out.println();
         src++;
      }
   }
}

Output

The graph created is:
0 -> 1	0 -> 2	0 -> 3	
1 -> 2	1 -> 4	2 -> 4	2 -> 3	
3 -> 1

Data Structure - Depth First Traversal

Depth First Search (DFS) algorithm traverses a graph in a depthward motion and uses a stack to remember to get the next vertex to start a search, when a dead end occurs in any iteration.

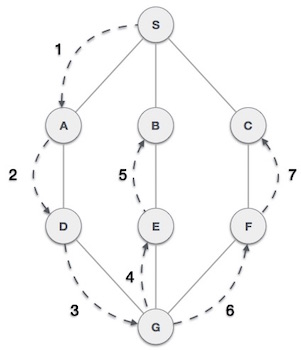
As in the example given above, DFS algorithm traverses from S to A to D to G to E to B first, then to F and lastly to C. It employs the following rules.

Rule 1 − Visit the adjacent unvisited vertex. Mark it as visited. Display it. Push it in a stack.
Rule 2 − If no adjacent vertex is found, pop up a vertex from the stack. (It will pop up all the vertices from the stack, which do not have adjacent vertices.)
Rule 3 − Repeat Rule 1 and Rule 2 until the stack is empty.

Step	Traversal	Description
1		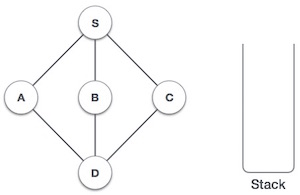Initialize the stack.
2		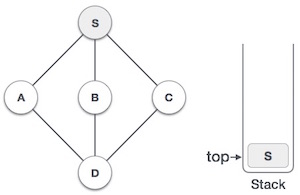Mark S as visited and put it onto the stack. Explore any unvisited adjacent node from S. We have three nodes and we can pick any of them. For this example, we shall take the node in an alphabetical order.
3		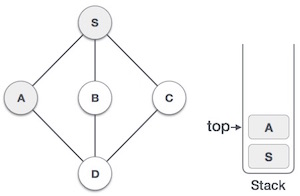Mark A as visited and put it onto the stack. Explore any unvisited adjacent node from A. Both S and D are adjacent to A but we are concerned for unvisited nodes only.
4		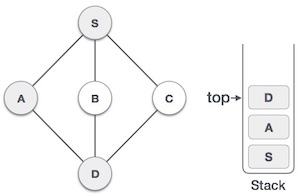Visit D and mark it as visited and put onto the stack. Here, we have B and C nodes, which are adjacent to D and both are unvisited. However, we shall again choose in an alphabetical order.
5		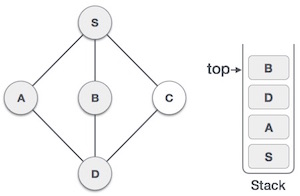We choose B, mark it as visited and put onto the stack. Here B does not have any unvisited adjacent node. So, we pop B from the stack.
6		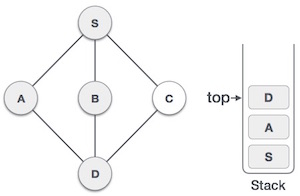We check the stack top for return to the previous node and check if it has any unvisited nodes. Here, we find D to be on the top of the stack.
7		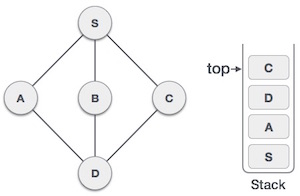Only unvisited adjacent node is from D is C now. So we visit C, mark it as visited and put it onto the stack.

As C does not have any unvisited adjacent node so we keep popping the stack until we find a node that has an unvisited adjacent node. In this case, there's none and we keep popping until the stack is empty.

To know about the implementation of this algorithm in C programming language, click here.

Data Structure - Breadth First Traversal

Breadth First Search (BFS) algorithm traverses a graph in a breadthward motion and uses a queue to remember to get the next vertex to start a search, when a dead end occurs in any iteration.

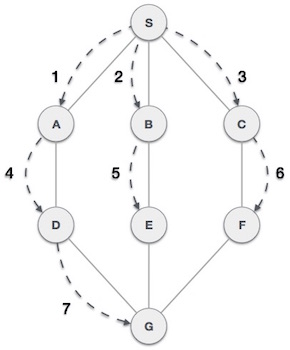
As in the example given above, BFS algorithm traverses from A to B to E to F first then to C and G lastly to D. It employs the following rules.

Rule 1 − Visit the adjacent unvisited vertex. Mark it as visited. Display it. Insert it in a queue.
Rule 2 − If no adjacent vertex is found, remove the first vertex from the queue.
Rule 3 − Repeat Rule 1 and Rule 2 until the queue is empty.

Step	Traversal	Description
1		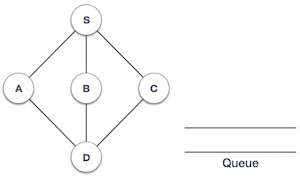Initialize the queue.
2		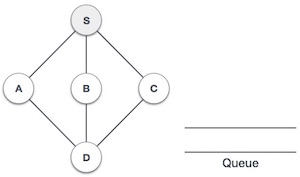We start from visiting S (starting node), and mark it as visited.
3		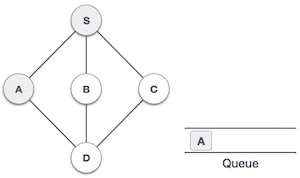We then see an unvisited adjacent node from S. In this example, we have three nodes but alphabetically we choose A, mark it as visited and enqueue it.
4		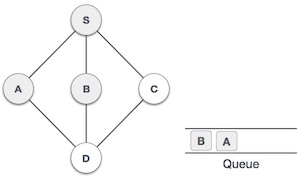Next, the unvisited adjacent node from S is B. We mark it as visited and enqueue it.
5		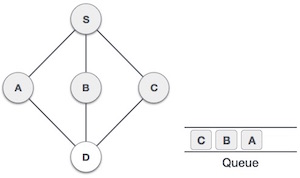Next, the unvisited adjacent node from S is C. We mark it as visited and enqueue it.
6		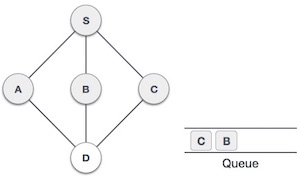Now, S is left with no unvisited adjacent nodes. So, we dequeue and find A.
7		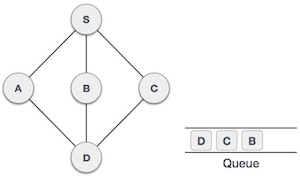From A we have D as unvisited adjacent node. We mark it as visited and enqueue it.

At this stage, we are left with no unmarked (unvisited) nodes. But as per the algorithm we keep on dequeuing in order to get all unvisited nodes. When the queue gets emptied, the program is over.

The implementation of this algorithm in C programming language can be seen here.

Data Structure and Algorithms - Tree

A tree is a non-linear abstract data type with a hierarchy-based structure. It consists of nodes (where the data is stored) that are connected via links. The tree data structure stems from a single node called a root node and has subtrees connected to the root.

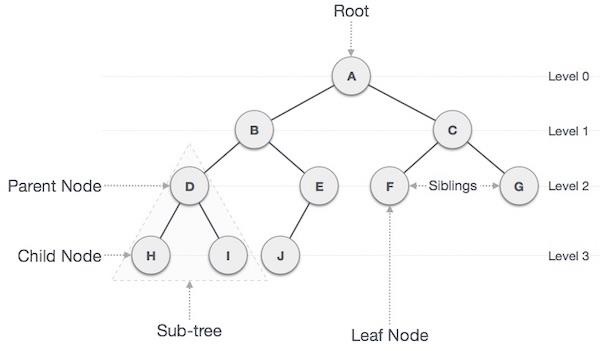
Important Terms

Following are the important terms with respect to tree.

Path − Path refers to the sequence of nodes along the edges of a tree.
Root − The node at the top of the tree is called root. There is only one root per tree and one path from the root node to any node.
Parent − Any node except the root node has one edge upward to a node called parent.
Child − The node below a given node connected by its edge downward is called its child node.
Leaf − The node which does not have any child node is called the leaf node.
Subtree − Subtree represents the descendants of a node.
Visiting − Visiting refers to checking the value of a node when control is on the node.
Traversing − Traversing means passing through nodes in a specific order.
Levels − Level of a node represents the generation of a node. If the root node is at level 0, then its next child node is at level 1, its grandchild is at level 2, and so on.
Keys − Key represents a value of a node based on which a search operation is to be carried out for a node.

Types of Trees

There are three types of trees −

General Trees
Binary Trees
Binary Search Trees

General Trees

General trees are unordered tree data structures where the root node has minimum 0 or maximum ‘n’ subtrees.

The General trees have no constraint placed on their hierarchy. The root node thus acts like the superset of all the other subtrees.

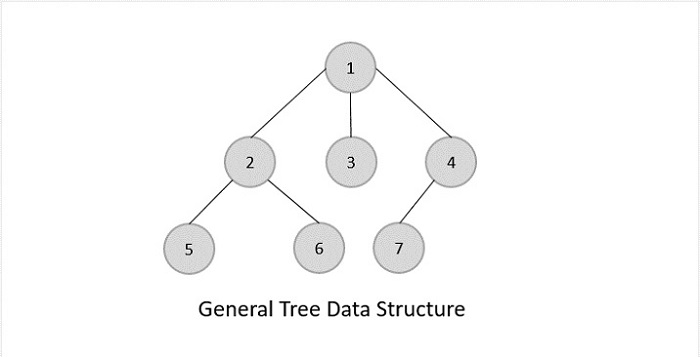
Binary Trees

Binary Trees are general trees in which the root node can only hold up to maximum 2 subtrees: left subtree and right subtree. Based on the number of children, binary trees are divided into three types.

Full Binary Tree

A full binary tree is a binary tree type where every node has either 0 or 2 child nodes.

Complete Binary Tree

A complete binary tree is a binary tree type where all the leaf nodes must be on the same level. However, root and internal nodes in a complete binary tree can either have 0, 1 or 2 child nodes.

Perfect Binary Tree

A perfect binary tree is a binary tree type where all the leaf nodes are on the same level and every node except leaf nodes have 2 children.

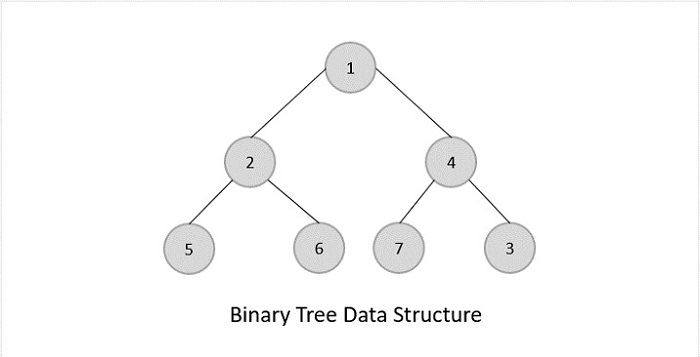
Binary Search Trees

Binary Search Trees possess all the properties of Binary Trees including some extra properties of their own, based on some constraints, making them more efficient than binary trees.

The data in the Binary Search Trees (BST) is always stored in such a way that the values in the left subtree are always less than the values in the root node and the values in the right subtree are always greater than the values in the root node, i.e. left subtree < root node ≤ right subtree.

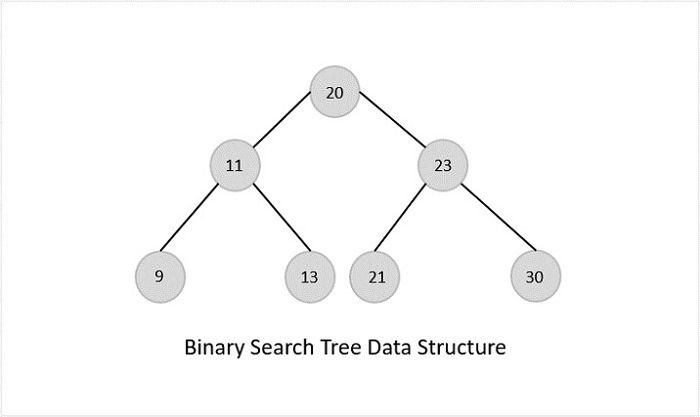
Advantages of BST

Binary Search Trees are more efficient than Binary Trees since time complexity for performing various operations reduces.
Since the order of keys is based on just the parent node, searching operation becomes simpler.
The alignment of BST also favors Range Queries, which are executed to find values existing between two keys. This helps in the Database Management System.

Disadvantages of BST

The main disadvantage of Binary Search Trees is that if all elements in nodes are either greater than or lesser than the root node, the tree becomes skewed. Simply put, the tree becomes slanted to one side completely.

This skewness will make the tree a linked list rather than a BST, since the worst case time complexity for searching operation becomes O(n).

To overcome this issue of skewness in the Binary Search Trees, the concept of Balanced Binary Search Trees was introduced.

Balanced Binary Search Trees

Consider a Binary Search Tree with ‘m’ as the height of the left subtree and ‘n’ as the height of the right subtree. If the value of (m-n) is equal to 0,1 or -1, the tree is said to be a Balanced Binary Search Tree.

The trees are designed in a way that they self-balance once the height difference exceeds 1. Binary Search Trees use rotations as self-balancing algorithms. There are four different types of rotations: Left Left, Right Right, Left Right, Right Left.

There are various types of self-balancing binary search trees −

AVL Trees
Red Black Trees
B Trees
B+ Trees
Splay Trees
Priority Search Trees

Data Structure & Algorithms - Tree Traversal

Traversal is a process to visit all the nodes of a tree and may print their values too. Because, all nodes are connected via edges (links) we always start from the root (head) node. That is, we cannot randomly access a node in a tree. There are three ways which we use to traverse a tree −

In-order Traversal
Pre-order Traversal
Post-order Traversal

Generally, we traverse a tree to search or locate a given item or key in the tree or to print all the values it contains.

In-order Traversal

In this traversal method, the left subtree is visited first, then the root and later the right sub-tree. We should always remember that every node may represent a subtree itself.

If a binary tree is traversed in-order, the output will produce sorted key values in an ascending order.

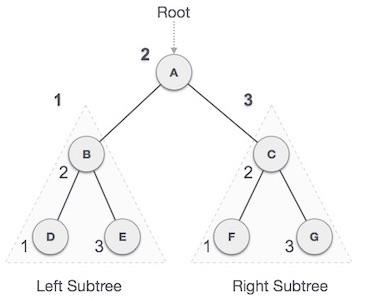
We start from A, and following in-order traversal, we move to its left subtree B.B is also traversed in-order. The process goes on until all the nodes are visited. The output of in-order traversal of this tree will be −

D → B → E → A → F → C → G

Algorithm

Until all nodes are traversed −

Step 1 − Recursively traverse left subtree.

Step 2 − Visit root node.

Step 3 − Recursively traverse right subtree.

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void inorder_traversal(struct node* root){
   if(root != NULL) {
      inorder_traversal(root->leftChild);
      printf("%d ",root->data);
      inorder_traversal(root->rightChild);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("\nInorder traversal: ");
   inorder_traversal(root);
   return 0;
}

Output

Inorder traversal: 10 14 19 27 31 35 42

#include <iostream>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void inorder_traversal(struct node* root){
   if(root != NULL) {
      inorder_traversal(root->leftChild);
      printf("%d ",root->data);
      inorder_traversal(root->rightChild);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("\nInorder traversal: ");
   inorder_traversal(root);
   return 0;
}

Output

Inorder traversal: 10 14 19 27 31 35 42

class Node {
   int data;
   Node leftChild;
   Node rightChild;
   public Node(int key) {
      data = key;
      leftChild = rightChild = null;
   }
}
public class TreeDataStructure {
   Node root = null;
   void inorder_traversal(Node node) {
      if(node != null) {
         inorder_traversal(node.leftChild);
         System.out.print(node.data + " ");
         inorder_traversal(node.rightChild);
      }
   }
   public static void main(String args[]) {
      TreeDataStructure tree = new TreeDataStructure();
      tree.root = new Node(27);
      tree.root.leftChild = new Node(12);
      tree.root.rightChild = new Node(3);
      tree.root.leftChild.leftChild = new Node(44);
      tree.root.leftChild.rightChild = new Node(17);
      tree.root.rightChild.leftChild = new Node(56);
      System.out.println("\nInorder traversal: ");
      tree.inorder_traversal(tree.root);
   }
}

Output

Inorder traversal: 
44 12 17 27 56 3

class Node:
   def __init__(self, key):
      self.leftChild = None
      self.rightChild = None
      self.data = key

# Create a function to perform inorder tree traversal
def InorderTraversal(root):
   if root:
      InorderTraversal(root.leftChild)
      print(root.data)
      InorderTraversal(root.rightChild)

# Main class
if __name__ == "__main__":
   root = Node(3)
   root.leftChild = Node(26)
   root.rightChild = Node(42)
   root.leftChild.leftChild = Node(54)
   root.leftChild.rightChild = Node(65)
   root.rightChild.leftChild = Node(12)

   # Function call
   print("\nInorder traversal of binary tree is")
   InorderTraversal(root)

Output

Inorder traversal of binary tree is
54
26
65
3
12
42

Pre-order Traversal

In this traversal method, the root node is visited first, then the left subtree and finally the right subtree.

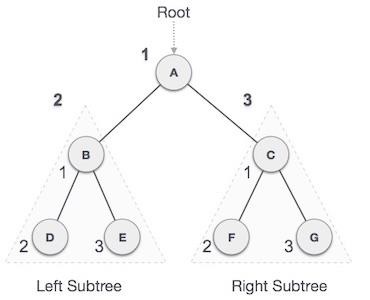
We start from A, and following pre-order traversal, we first visit A itself and then move to its left subtree B. B is also traversed pre-order. The process goes on until all the nodes are visited. The output of pre-order traversal of this tree will be −

A → B → D → E → C → F → G

Algorithm

Until all nodes are traversed −

Step 1 − Visit root node.

Step 2 − Recursively traverse left subtree.

Step 3 − Recursively traverse right subtree.

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void pre_order_traversal(struct node* root){
   if(root != NULL) {
      printf("%d ",root->data);
      pre_order_traversal(root->leftChild);
      pre_order_traversal(root->rightChild);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("\nPreorder traversal: ");
   pre_order_traversal(root);
   return 0;
}

Output

Preorder traversal: 27 14 10 19 35 31 42

#include <iostream>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void pre_order_traversal(struct node* root){
   if(root != NULL) {
      printf("%d ",root->data);
      pre_order_traversal(root->leftChild);
      pre_order_traversal(root->rightChild);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("\nPreorder traversal: ");
   pre_order_traversal(root);
   return 0;
}

Output

Preorder traversal: 27 14 10 19 35 31 42

class Node {
   int data;
   Node leftChild;
   Node rightChild;
   public Node(int key) {
      data = key;
      leftChild = rightChild = null;
   }
}
public class TreeDataStructure {
   Node root = null;
   void pre_order_traversal(Node node) {
      if(node != null) {
         System.out.print(node.data + " ");
         pre_order_traversal(node.leftChild);
         pre_order_traversal(node.rightChild);
      }
   }
   public static void main(String args[]) {
      TreeDataStructure tree = new TreeDataStructure();
      tree.root = new Node(27);
      tree.root.leftChild = new Node(12);
      tree.root.rightChild = new Node(3);
      tree.root.leftChild.leftChild = new Node(44);
      tree.root.leftChild.rightChild = new Node(17);
      tree.root.rightChild.leftChild = new Node(56);
      System.out.println("\nPreorder traversal: ");
      tree.pre_order_traversal(tree.root);
   }
}

Output

Preorder traversal: 
27 12 44 17 3 56

class Node:
   def __init__(self, key):
      self.leftChild = None
      self.rightChild = None
      self.data = key

# Create a function to perform postorder tree traversal
def PreorderTraversal(root):
   if root:
      print(root.data)
      PreorderTraversal(root.leftChild)
      PreorderTraversal(root.rightChild)

# Main class
if __name__ == "__main__":
   root = Node(3)
   root.leftChild = Node(26)
   root.rightChild = Node(42)
   root.leftChild.leftChild = Node(54)
   root.leftChild.rightChild = Node(65)
   root.rightChild.leftChild = Node(12)
   print("\nPreorder traversal of binary tree is")
   PreorderTraversal(root)

Output

Preorder traversal of binary tree is
3
26
54
65
42
12

Post-order Traversal

In this traversal method, the root node is visited last, hence the name. First we traverse the left subtree, then the right subtree and finally the root node.

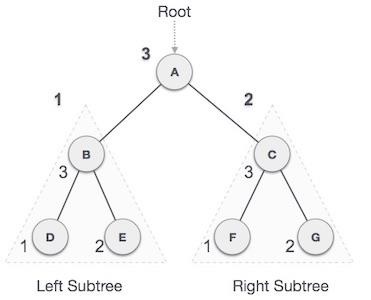
We start from A, and following pre-order traversal, we first visit the left subtree B. B is also traversed post-order. The process goes on until all the nodes are visited. The output of post-order traversal of this tree will be −

D → E → B → F → G → C → A

Algorithm

Until all nodes are traversed −

Step 1 − Recursively traverse left subtree.

Step 2 − Recursively traverse right subtree.

Step 3 − Visit root node.

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void post_order_traversal(struct node* root){
   if(root != NULL) {
      post_order_traversal(root->leftChild);
      post_order_traversal(root->rightChild);
      printf("%d ", root->data);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("\nPost order traversal: ");
   post_order_traversal(root);
   return 0;
}

Output

Post order traversal: 10 19 14 31 42 35 27

#include <iostream>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void post_order_traversal(struct node* root){
   if(root != NULL) {
      post_order_traversal(root->leftChild);
      post_order_traversal(root->rightChild);
      printf("%d ", root->data);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("\nPost order traversal: ");
   post_order_traversal(root);
   return 0;
}

Output

Post order traversal: 10 19 14 31 42 35 27

class Node {
   int data;
   Node leftChild;
   Node rightChild;
   public Node(int key) {
      data = key;
      leftChild = rightChild = null;
   }
}
public class TreeDataStructure {
   Node root = null;
   void post_order_traversal(Node node) {
      if(node != null) {
         post_order_traversal(node.leftChild);
         post_order_traversal(node.rightChild);
         System.out.print(node.data + " ");
      }
   }
   public static void main(String args[]) {
      TreeDataStructure tree = new TreeDataStructure();
      tree.root = new Node(27);
      tree.root.leftChild = new Node(12);
      tree.root.rightChild = new Node(3);
      tree.root.leftChild.leftChild = new Node(44);
      tree.root.leftChild.rightChild = new Node(17);
      tree.root.rightChild.leftChild = new Node(56);
      System.out.println("\nPost order traversal: ");
      tree.post_order_traversal(tree.root);
   }
}

Output

Post order traversal: 
44 17 12 56 3 27

class Node:
   def __init__(self, key):
      self.leftChild = None
      self.rightChild = None
      self.data = key

# Create a function to perform preorder tree traversal
def PostorderTraversal(root):
   if root:
      PostorderTraversal(root.leftChild)
      PostorderTraversal(root.rightChild)
      print(root.data)

# Main class
if __name__ == "__main__":
   root = Node(3)
   root.leftChild = Node(26)
   root.rightChild = Node(42)
   root.leftChild.leftChild = Node(54)
   root.leftChild.rightChild = Node(65)
   root.rightChild.leftChild = Node(12)
   print("\nPostorder traversal of binary tree is")
   PostorderTraversal(root)

Output

Postorder traversal of binary tree is
54
65
26
12
42
3

To check the C implementation of tree traversing, please click here

Implementation

In-order Traversal
Pre-order Traversal
Post-order Traversal

We shall now see the implementation of tree traversal in C programming language here using the following binary tree −

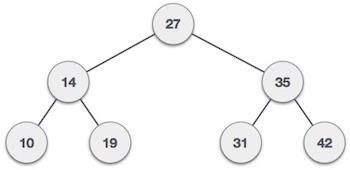
Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

//if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void pre_order_traversal(struct node* root){
   if(root != NULL) {
      printf("%d ",root->data);
      pre_order_traversal(root->leftChild);
      pre_order_traversal(root->rightChild);
   }
}
void inorder_traversal(struct node* root){
   if(root != NULL) {
      inorder_traversal(root->leftChild);
      printf("%d ",root->data);
      inorder_traversal(root->rightChild);
   }
}
void post_order_traversal(struct node* root){
   if(root != NULL) {
      post_order_traversal(root->leftChild);
      post_order_traversal(root->rightChild);
      printf("%d ", root->data);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("\nPreorder traversal: ");
   pre_order_traversal(root);
   printf("\nInorder traversal: ");
   inorder_traversal(root);
   printf("\nPost order traversal: ");
   post_order_traversal(root);
   return 0;
}

Output

Preorder traversal: 27 14 10 19 35 31 42 
Inorder traversal: 10 14 19 27 31 35 42 
Post order traversal: 10 19 14 31 42 35 27

#include <iostream>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void pre_order_traversal(struct node* root){
   if(root != NULL) {
      printf("%d ",root->data);
      pre_order_traversal(root->leftChild);
      pre_order_traversal(root->rightChild);
   }
}
void inorder_traversal(struct node* root){
   if(root != NULL) {
      inorder_traversal(root->leftChild);
      printf("%d ",root->data);
      inorder_traversal(root->rightChild);
   }
}
void post_order_traversal(struct node* root){
   if(root != NULL) {
      post_order_traversal(root->leftChild);
      post_order_traversal(root->rightChild);
      printf("%d ", root->data);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("\nPreorder traversal: ");
   pre_order_traversal(root);
   printf("\nInorder traversal: ");
   inorder_traversal(root);
   printf("\nPost order traversal: ");
   post_order_traversal(root);
   return 0;
}

Output

Preorder traversal: 27 14 10 19 35 31 42 
Inorder traversal: 10 14 19 27 31 35 42 
Post order traversal: 10 19 14 31 42 35 27

class Node {
   int data;
   Node leftChild;
   Node rightChild;
   public Node(int key) {
      data = key;
      leftChild = rightChild = null;
   }
}
public class TreeDataStructure {
   Node root = null;
   void inorder_traversal(Node node) {
      if(node != null) {
         inorder_traversal(node.leftChild);
         System.out.print(node.data + " ");
         inorder_traversal(node.rightChild);
      }
   }
   void pre_order_traversal(Node node) {
      if(node != null) {
         System.out.print(node.data + " ");
         pre_order_traversal(node.leftChild);
         pre_order_traversal(node.rightChild);
      }
   }
   void post_order_traversal(Node node) {
      if(node != null) {
         post_order_traversal(node.leftChild);
         post_order_traversal(node.rightChild);
         System.out.print(node.data + " ");
      }
   }
   public static void main(String args[]) {
      TreeDataStructure tree = new TreeDataStructure();
      tree.root = new Node(27);
      tree.root.leftChild = new Node(12);
      tree.root.rightChild = new Node(3);
      tree.root.leftChild.leftChild = new Node(44);
      tree.root.leftChild.rightChild = new Node(17);
      tree.root.rightChild.leftChild = new Node(56);
      System.out.println("\nInorder traversal: ");
      tree.inorder_traversal(tree.root);
      System.out.println("\nPreorder traversal: ");
      tree.pre_order_traversal(tree.root);
      System.out.println("\nPost order traversal: ");
      tree.post_order_traversal(tree.root);
   }
}

Output

Inorder traversal: 
44 12 17 27 56 3 
Preorder traversal: 
27 12 44 17 3 56 
Post order traversal: 
44 17 12 56 3 27

class Node:
   def __init__(self, key):
      self.leftChild = None
      self.rightChild = None
      self.data = key

# Create a function to perform inorder tree traversal
def InorderTraversal(root):
   if root:
      InorderTraversal(root.leftChild)
      print(root.data)
      InorderTraversal(root.rightChild)

# Create a function to perform preorder tree traversal
def PostorderTraversal(root):
   if root:
      PostorderTraversal(root.leftChild)
      PostorderTraversal(root.rightChild)
      print(root.data)

# Create a function to perform postorder tree traversal
def PreorderTraversal(root):
   if root:
      print(root.data)
      PreorderTraversal(root.leftChild)
      PreorderTraversal(root.rightChild)

# Main class
if __name__ == "__main__":
   root = Node(3)
   root.leftChild = Node(26)
   root.rightChild = Node(42)
   root.leftChild.leftChild = Node(54)
   root.leftChild.rightChild = Node(65)
   root.rightChild.leftChild = Node(12)

   # Function call
   print("\nInorder traversal of binary tree is")
   InorderTraversal(root)
   print("\nPreorder traversal of binary tree is")
   PreorderTraversal(root)
   print("\nPostorder traversal of binary tree is")
   PostorderTraversal(root)

Output

Inorder traversal of binary tree is
54
26
65
3
12
42

Preorder traversal of binary tree is
3
26
54
65
42
12

Postorder traversal of binary tree is
54
65
26
12
42
3

Data Structure - Binary Search Tree

A Binary Search Tree (BST) is a tree in which all the nodes follow the below-mentioned properties −

The left sub-tree of a node has a key less than or equal to its parent node's key.
The right sub-tree of a node has a key greater than or equal to its parent node's key.

Thus, BST divides all its sub-trees into two segments; the left sub-tree and the right sub-tree and can be defined as −

left_subtree (keys) ≤ node (key) ≤ right_subtree (keys)

Representation

BST is a collection of nodes arranged in a way where they maintain BST properties. Each node has a key and an associated value. While searching, the desired key is compared to the keys in BST and if found, the associated value is retrieved.

Following is a pictorial representation of BST −

We observe that the root node key (27) has all less-valued keys on the left sub-tree and the higher valued keys on the right sub-tree.

Basic Operations

Following are the basic operations of a tree −

Search − Searches an element in a tree.
Insert − Inserts an element in a tree.
Pre-order Traversal − Traverses a tree in a pre-order manner.
In-order Traversal − Traverses a tree in an in-order manner.
Post-order Traversal − Traverses a tree in a post-order manner.

Defining a Node

Define a node that stores some data, and references to its left and right child nodes.

struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};

Search Operation

Whenever an element is to be searched, start searching from the root node. Then if the data is less than the key value, search for the element in the left subtree. Otherwise, search for the element in the right subtree. Follow the same algorithm for each node.

Algorithm

1. START
2. Check whether the tree is empty or not
3. If the tree is empty, search is not possible
4. Otherwise, first search the root of the tree.
5. If the key does not match with the value in the root, search its subtrees.
6. If the value of the key is less than the root value, search the left subtree
7. If the value of the key is greater than the root value, search the right subtree.
8. If the key is not found in the tree, return unsuccessful search.
9. END

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild, *rightChild;
};
struct node *root = NULL;
struct node *newNode(int item){
   struct node *temp = (struct node *)malloc(sizeof(struct node));
   temp->data = item;
   temp->leftChild = temp->rightChild = NULL;
   return temp;
}
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;
   
   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;
         
         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;
            
            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;
            
            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
struct node* search(int data){
   struct node *current = root;
   printf("\nVisiting elements: ");
   while(current->data != data) {
      if(current != NULL) {
         printf("%d ",current->data);
         
         //go to left tree
         if(current->data > data) {
            current = current->leftChild;
         }//else go to right tree
         else {
            current = current->rightChild;
         }
         
         //not found
         if(current == NULL) {
            return NULL;
         }
      }
   }
   return current;
}
void printTree(struct node* Node){
   if(Node == NULL)
      return;
   printTree(Node->leftChild);
   printf(" --%d", Node->data);
   printTree(Node->rightChild);
}
int main(){
   insert(55);
   insert(20);
   insert(90);
   insert(50);
   insert(35);
   insert(15);
   insert(65);
   printf("Insertion done\n");
   printTree(root);
   struct node* k;
   k = search(35);
   if(k != NULL)
      printf("\nElement %d found", k->data);
   else
      printf("\nElement not found");
   return 0;
}

Output

Insertion done
 --15 --20 --35 --50 --55 --65 --90
Visiting elements: 55 20 50 
Element 35 found

#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild, *rightChild;
};
struct node *root = NULL;
struct node *newNode(int item){
   struct node *temp = (struct node *)malloc(sizeof(struct node));
   temp->data = item;
   temp->leftChild = temp->rightChild = NULL;
   return temp;
}
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;
   
   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;
         
         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;
            
            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;
            
            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
struct node* search(int data){
   struct node *current = root;
   printf("\nVisiting elements: ");
   while(current->data != data) {
      if(current != NULL) {
         printf("%d ",current->data);
         
         //go to left tree
         if(current->data > data) {
            current = current->leftChild;
         }//else go to right tree
         else {
            current = current->rightChild;
         }
         
         //not found
         if(current == NULL) {
            return NULL;
         }
      }
   }
   return current;
}
void printTree(struct node* Node){
   if(Node == NULL)
      return;
   printTree(Node->leftChild);
   printf(" --%d", Node->data);
   printTree(Node->rightChild);
}
int main(){
   insert(55);
   insert(20);
   insert(90);
   insert(50);
   insert(35);
   insert(15);
   insert(65);
   printf("Insertion done\n");
   printTree(root);
   struct node* k;
   k = search(35);
   if(k != NULL)
      printf("\nElement %d found", k->data);
   else
      printf("\nElement not found");
   return 0;
}

Output

Insertion done
 --15 --20 --35 --50 --55 --65 --90
Visiting elements: 55 20 50 
Element 35 found

import java.util.Scanner;
class BSTNode {
   BSTNode left, right;
   int data;
   public BSTNode(int n) {
      left = null;
      right = null;
      data = n;
   }
}
public class BST {
   static BSTNode root;
   public BST() {
      root = null;
   }
   private BSTNode insert(BSTNode node, int data) {
      if(node == null)
         node = new BSTNode(data);
      else {
         if(data <= node.data)
            node.left = insert(node.left, data);
         else
            node.right = insert(node.right, data);
      }
      return node;
   }
   private boolean search(BSTNode r, int val) {
      boolean found = false;
      while ((r != null) && !found) {
         int rval = r.data;
         if(val < rval)
            r = r.left;
         else if (val > rval)
            r = r.right;
         else {
            found = true;
            break;
         }
         found = search(r, val);
      }
      return found;
   }
   void printTree(BSTNode node, String prefix) {
      if(node == null)
         return;
      printTree(node.left , " " + prefix);
      System.out.println(prefix + "--" + node.data);
      printTree(node.right , prefix + " ");
   }
   public static void main(String args[]) {
      Scanner sc = new Scanner(System.in);
      BST bst = new BST();
      root = bst.insert(root, 55);
      root = bst.insert(root, 20);
      root = bst.insert(root, 90);
      root = bst.insert(root, 80);
      root = bst.insert(root, 50);
      root = bst.insert(root, 35);
      root = bst.insert(root, 15);
      root = bst.insert(root, 65);
      bst.printTree(root, " ");
      System.out.println("Element found = " + bst.search(root, 80));
   }
}

Output

--15
  --20--35
   --50
 --55
    --65
   --80
  --90
Element found = true

class Node:
   def __init__(self, data):
      self.left = None
      self.right = None
      self.data = data

# Insert method to create nodes
   def insert(self, data):
      if self.data:
         if data < self.data:
            if self.left is None:
               self.left = Node(data)
            else:
               self.left.insert(data)
         elif data > self.data:
            if self.right is None:
               self.right = Node(data)
            else:
               self.right.insert(data)
         else:
            self.data = data
# search method to compare the value with nodes
   def search(self, key):
      if key < self.data:
         if self.left is None:
            return str(key)+" Not Found"
         return self.left.search(key)
      elif key > self.data:
         if self.right is None:
            return str(key)+" Not Found"
         return self.right.search(key)
      else:
         print(str(self.data) + ' is found')

root = Node(54)
root.insert(34)
root.insert(46)
root.insert(12)
root.insert(23)
root.insert(5)
print(root.search(17))
print(root.search(12))

Output

17 Not Found
12 is found
None

Insert Operation

Whenever an element is to be inserted, first locate its proper location. Start searching from the root node, then if the data is less than the key value, search for the empty location in the left subtree and insert the data. Otherwise, search for the empty location in the right subtree and insert the data.

Algorithm

1 – START
2 – If the tree is empty, insert the first element as the root node of the tree. The following elements are added as the leaf nodes.
3 – If an element is less than the root value, it is added into the left subtree as a leaf node.
4 – If an element is greater than the root value, it is added into the right subtree as a leaf node.
5 – The final leaf nodes of the tree point to NULL values as their child nodes.
6 – END

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild, *rightChild;
};
struct node *root = NULL;
struct node *newNode(int item){
   struct node *temp = (struct node *)malloc(sizeof(struct node));
   temp->data = item;
   temp->leftChild = temp->rightChild = NULL;
   return temp;
}
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;
   
   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;
         
         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;
            
            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;
            
            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void printTree(struct node* Node){
   if(Node == NULL)
      return;
   printTree(Node->leftChild);
   printf(" --%d", Node->data);
   printTree(Node->rightChild);
}
int main(){
   insert(55);
   insert(20);
   insert(90);
   insert(50);
   insert(35);
   insert(15);
   insert(65);
   printf("Insertion done\n");
   printTree(root);
   return 0;
}

Output

Insertion done
 --15 --20 --35 --50 --55 --65 --90

#include <iostream>
struct node {
   int data;
   struct node *leftChild, *rightChild;
};
struct node *root = NULL;
struct node *newNode(int item){
   struct node *temp = (struct node *)malloc(sizeof(struct node));
   temp->data = item;
   temp->leftChild = temp->rightChild = NULL;
   return temp;
}
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;
   
   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;
         
         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;
            
            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;
            
            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void printTree(struct node* Node){
   if(Node == NULL)
      return;
   printTree(Node->leftChild);
   printf(" --%d", Node->data);
   printTree(Node->rightChild);
}
int main(){
   insert(55);
   insert(20);
   insert(90);
   insert(50);
   insert(35);
   insert(15);
   insert(65);
   printf("Insertion done\n");
   printTree(root);
   return 0;
}

Output

Insertion done
 --15 --20 --35 --50 --55 --65 --90

import java.util.Scanner;
class BSTNode {
   BSTNode left, right;
   int data;
   public BSTNode(int n) {
      left = null;
      right = null;
      data = n;
   }
}
public class BST {
   static BSTNode root;
   public BST() {
      root = null;
   }
   private BSTNode insert(BSTNode node, int data) {
      if(node == null)
         node = new BSTNode(data);
      else {
         if(data <= node.data)
            node.left = insert(node.left, data);
         else
            node.right = insert(node.right, data);
      }
      return node;
   }
   void printTree(BSTNode node, String prefix) {
      if(node == null)
         return;
      printTree(node.left , " " + prefix);
      System.out.println(prefix + "--" + node.data);
      printTree(node.right , prefix + " ");
   }
   public static void main(String args[]) {
      Scanner sc = new Scanner(System.in);
      BST bst = new BST();
      root = bst.insert(root, 55);
      root = bst.insert(root, 20);
      root = bst.insert(root, 90);
      root = bst.insert(root, 80);
      root = bst.insert(root, 50);
      root = bst.insert(root, 35);
      root = bst.insert(root, 15);
      root = bst.insert(root, 65);
      bst.printTree(root, " ");
   }
}

Output

--15
  --20
--35
   --50
 --55
    --65
   --80
  --90

class Node:
   def __init__(self, data):
      self.left = None
      self.right = None
      self.data = data

# Insert method to create nodes
   def insert(self, data):
      if self.data:
         if data < self.data:
            if self.left is None:
               self.left = Node(data)
            else:
               self.left.insert(data)
         elif data > self.data:
            if self.right is None:
               self.right = Node(data)
            else:
               self.right.insert(data)
         else:
            self.data = data
root = Node(54)
root.insert(34)
root.insert(46)
root.insert(12)
root.insert(23)
root.insert(5)
print("Insertion Done")

Output

Insertion Done

Inorder Traversal

The inorder traversal operation in a Binary Search Tree visits all its nodes in the following order −

Firstly, we traverse the left child of the root node/current node, if any.
Next, traverse the current node.
Lastly, traverse the right child of the current node, if any.

Algorithm

1. START
2. Traverse the left subtree, recursively
3. Then, traverse the root node
4. Traverse the right subtree, recursively.
5. END

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
#include <stdlib.h>
struct node {
   int key;
   struct node *left, *right;
};
struct node *newNode(int item){
   struct node *temp = (struct node *)malloc(sizeof(struct node));
   temp->key = item;
   temp->left = temp->right = NULL;
   return temp;
}

// Inorder Traversal
void inorder(struct node *root){
   if (root != NULL) {
      inorder(root->left);
      printf("%d -> ", root->key);
      inorder(root->right);
   }
}

// Insertion operation
struct node *insert(struct node *node, int key){
   if (node == NULL) return newNode(key);
   if (key < node->key)
      node->left = insert(node->left, key);
   else
      node->right = insert(node->right, key);
   return node;
}
int main(){
   struct node *root = NULL;
   root = insert(root, 55);
   root = insert(root, 20);
   root = insert(root, 90);
   root = insert(root, 50);
   root = insert(root, 35);
   root = insert(root, 15);
   root = insert(root, 65);
   printf("Inorder traversal: ");
   inorder(root);
}

Output

Inorder traversal: 15 -> 20 -> 35 -> 50 -> 55 -> 65 -> 90 ->

#include <iostream>
struct node {
   int key;
   struct node *left, *right;
};
struct node *newNode(int item){
   struct node *temp = (struct node *)malloc(sizeof(struct node));
   temp->key = item;
   temp->left = temp->right = NULL;
   return temp;
}

// Inorder Traversal
void inorder(struct node *root){
   if (root != NULL) {
     inorder(root->left);
     printf("%d -> ", root->key);
     inorder(root->right);
   }
}

// Insertion operation
struct node *insert(struct node *node, int key){
   if (node == NULL) return newNode(key);
   if (key < node->key)
     node->left = insert(node->left, key);
   else
     node->right = insert(node->right, key);
   return node;
}
int main(){
   struct node *root = NULL;
   root = insert(root, 55);
   root = insert(root, 20);
   root = insert(root, 90);
   root = insert(root, 50);
   root = insert(root, 35);
   root = insert(root, 15);
   root = insert(root, 65);
   printf("Inorder traversal: ");
   inorder(root);
}

Output

Inorder traversal: 15 -> 20 -> 35 -> 50 -> 55 -> 65 -> 90 ->

class Node {
   int data;
   Node leftChild;
   Node rightChild;
   public Node(int key) {
      data = key;
      leftChild = rightChild = null;
   }
}
public class TreeDataStructure {
   Node root = null;
   void inorder_traversal(Node node) {
      if(node != null) {
         inorder_traversal(node.leftChild);
         System.out.print(node.data + " ");
         inorder_traversal(node.rightChild);
      }
   }
   public static void main(String args[]) {
      TreeDataStructure tree = new TreeDataStructure();
      tree.root = new Node(27);
      tree.root.leftChild = new Node(12);
      tree.root.rightChild = new Node(30);
      tree.root.leftChild.leftChild = new Node(4);
      tree.root.leftChild.rightChild = new Node(17);
      tree.root.rightChild.leftChild = new Node(56);
      System.out.println("\nInorder traversal: ");
      tree.inorder_traversal(tree.root);
   }
}

Output

Inorder traversal:
4 12 17 27 56 30

class Node:
   def __init__(self, data):
      self.left = None
      self.right = None
      self.data = data

# Insert method to create nodes
   def insert(self, data):
      if self.data:
         if data < self.data:
            if self.left is None:
               self.left = Node(data)
            else:
               self.left.insert(data)
         elif data > self.data:
            if self.right is None:
               self.right = Node(data)
            else:
               self.right.insert(data)
         else:
            self.data = data

# Print the tree
   def Inorder(self):
      if self.left:
         self.left.Inorder()
         print(self.data)
      if self.right:
         self.right.Inorder()

root = Node(54)
root.insert(34)
root.insert(46)
root.insert(12)
root.insert(23)
root.insert(5)
print("Inorder Traversal of Binary Search Tree: ")
root.Inorder()

Output

Inorder Traversal of Binary Search Tree: 
12
34
54

Preorder Traversal

The preorder traversal operation in a Binary Search Tree visits all its nodes. However, the root node in it is first printed, followed by its left subtree and then its right subtree.

Algorithm

1. START
2. Traverse the root node first.
3. Then traverse the left subtree, recursively
4. Later, traverse the right subtree, recursively.
5. END

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
#include <stdlib.h>
struct node {
   int key;
   struct node *left, *right;
};
struct node *newNode(int item){
   struct node *temp = (struct node *)malloc(sizeof(struct node));
   temp->key = item;
   temp->left = temp->right = NULL;
   return temp;
}

// Preorder Traversal
void preorder(struct node *root){
   if (root != NULL) {
      printf("%d -> ", root->key);
      preorder(root->left);
      preorder(root->right);
   }
}

// Insertion operation
struct node *insert(struct node *node, int key){
   if (node == NULL) return newNode(key);
   if (key < node->key)
      node->left = insert(node->left, key);
   else
      node->right = insert(node->right, key);
   return node;
}
int main(){
   struct node *root = NULL;
   root = insert(root, 55);
   root = insert(root, 20);
   root = insert(root, 90);
   root = insert(root, 50);
   root = insert(root, 35);
   root = insert(root, 15);
   root = insert(root, 65);
   printf("Preorder traversal: ");
   preorder(root);
}

Output

Preorder traversal: 55 -> 20 -> 15 -> 50 -> 35 -> 90 -> 65 ->

#include <iostream>
struct node {
   int key;
   struct node *left, *right;
};
struct node *newNode(int item){
   struct node *temp = (struct node *)malloc(sizeof(struct node));
   temp->key = item;
   temp->left = temp->right = NULL;
   return temp;
}

// Preorder Traversal
void preorder(struct node *root){
   if (root != NULL) {
      printf("%d -> ", root->key);
      preorder(root->left);
      preorder(root->right);
   }
}

// Insertion operation
struct node *insert(struct node *node, int key){
   if (node == NULL) return newNode(key);
   if (key < node->key)
      node->left = insert(node->left, key);
   else
      node->right = insert(node->right, key);
   return node;
}
int main(){
   struct node *root = NULL;
   root = insert(root, 55);
   root = insert(root, 20);
   root = insert(root, 90);
   root = insert(root, 50);
   root = insert(root, 35);
   root = insert(root, 15);
   root = insert(root, 65);
   printf("Preorder traversal: ");
   preorder(root);
}

Output

Preorder traversal: 55 -> 20 -> 15 -> 50 -> 35 -> 90 -> 65 ->

class Node {
    int data;
    Node leftChild;
    Node rightChild;
    public Node(int key) {
        data = key;
        leftChild = rightChild = null;
    }
}
public class TreeDataStructure {
    Node root = null;
    void preorder_traversal(Node node) {
        if(node != null) {
            System.out.print(node.data + " ");
            preorder_traversal(node.leftChild);
            preorder_traversal(node.rightChild);
        }
    }
    public static void main(String args[]) {
        TreeDataStructure tree = new TreeDataStructure();
        tree.root = new Node(27);
        tree.root.leftChild = new Node(12);
        tree.root.rightChild = new Node(30);
        tree.root.leftChild.leftChild = new Node(4);
        tree.root.leftChild.rightChild = new Node(17);
        tree.root.rightChild.leftChild = new Node(56);
        System.out.println("\nPreorder traversal: ");
        tree.preorder_traversal(tree.root);
    }
}

Output

Preorder traversal: 
27 12 4 17 30 56

class Node:
   def __init__(self, data):
      self.left = None
      self.right = None
      self.data = data

# Insert method to create nodes
   def insert(self, data):
      if self.data:
         if data < self.data:
            if self.left is None:
               self.left = Node(data)
            else:
               self.left.insert(data)
         elif data > self.data:
            if self.right is None:
               self.right = Node(data)
            else:
               self.right.insert(data)
         else:
            self.data = data

# Print the tree
   def Preorder(self):
      print(self.data)
      if self.left:
         self.left.Preorder()
      if self.right:
         self.right.Preorder()
root = Node(54)
root.insert(34)
root.insert(46)
root.insert(12)
root.insert(23)
root.insert(5)
print("Preorder Traversal of Binary Search Tree: ")
root.Preorder()

Output

Preorder Traversal of Binary Search Tree: 
54
34
12
5
23
46

Postorder Traversal

Like the other traversals, postorder traversal also visits all the nodes in a Binary Search Tree and displays them. However, the left subtree is printed first, followed by the right subtree and lastly, the root node.

Algorithm

1. START
2. Traverse the left subtree, recursively
3. Traverse the right subtree, recursively.
4. Then, traverse the root node
5. END

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
#include <stdlib.h>
struct node {
   int key;
   struct node *left, *right;
};
struct node *newNode(int item){
   struct node *temp = (struct node *)malloc(sizeof(struct node));
   temp->key = item;
   temp->left = temp->right = NULL;
   return temp;
}

// Postorder Traversal
void postorder(struct node *root){
   if (root != NULL) {
      printf("%d -> ", root->key);
      postorder(root->left);
      postorder(root->right);
   }
}

// Insertion operation
struct node *insert(struct node *node, int key){
   if (node == NULL) return newNode(key);
   if (key < node->key)
      node->left = insert(node->left, key);
   else
      node->right = insert(node->right, key);
   return node;
}
int main(){
   struct node *root = NULL;
   root = insert(root, 55);
   root = insert(root, 20);
   root = insert(root, 90);
   root = insert(root, 50);
   root = insert(root, 35);
   root = insert(root, 15);
   root = insert(root, 65);
   printf("Postorder traversal: ");
   postorder(root);
}

Output

Postorder traversal: 55 -> 20 -> 15 -> 50 -> 35 -> 90 -> 65 ->

#include <iostream>
struct node {
   int key;
   struct node *left, *right;
};
struct node *newNode(int item){
   struct node *temp = (struct node *)malloc(sizeof(struct node));
   temp->key = item;
   temp->left = temp->right = NULL;
   return temp;
}

// Postorder Traversal
void postorder(struct node *root){
   if (root != NULL) {
      printf("%d -> ", root->key);
      postorder(root->left);
      postorder(root->right);
   }
}

// Insertion operation
struct node *insert(struct node *node, int key){
   if (node == NULL) return newNode(key);
   if (key < node->key)
      node->left = insert(node->left, key);
   else
      node->right = insert(node->right, key);
   return node;
}
int main(){
   struct node *root = NULL;
   root = insert(root, 55);
   root = insert(root, 20);
   root = insert(root, 90);
   root = insert(root, 50);
   root = insert(root, 35);
   root = insert(root, 15);
   root = insert(root, 65);
   printf("Postorder traversal: ");
   postorder(root);
}

Output

Postorder traversal: 55 -> 20 -> 15 -> 50 -> 35 -> 90 -> 65 ->

class Node {
    int data;
    Node leftChild;
    Node rightChild;
    public Node(int key) {
        data = key;
        leftChild = rightChild = null;
    }
}
public class TreeDataStructure {
    Node root = null;
    void postorder_traversal(Node node) {
        if(node != null) {
            postorder_traversal(node.leftChild);
            postorder_traversal(node.rightChild);
            System.out.print(node.data + " ");
        }
    }
    public static void main(String args[]) {
        TreeDataStructure tree = new TreeDataStructure();
        tree.root = new Node(27);
        tree.root.leftChild = new Node(12);
        tree.root.rightChild = new Node(30);
        tree.root.leftChild.leftChild = new Node(4);
        tree.root.leftChild.rightChild = new Node(17);
        tree.root.rightChild.leftChild = new Node(56);
        System.out.println("\nPostorder traversal: ");
        tree.postorder_traversal(tree.root);
    }
}

Output

Postorder traversal: 
4 17 12 56 30 27

class Node:
   def __init__(self, data):
      self.left = None
      self.right = None
      self.data = data

# Insert method to create nodes
   def insert(self, data):
      if self.data:
         if data < self.data:
            if self.left is None:
               self.left = Node(data)
            else:
               self.left.insert(data)
         elif data > self.data:
            if self.right is None:
               self.right = Node(data)
            else:
               self.right.insert(data)
      else:
         self.data = data

# Print the tree
   def Postorder(self):
      if self.left:
         self.left.Postorder()
      if self.right:
         self.right.Postorder()
      print(self.data)

root = Node(54)
root.insert(34)
root.insert(46)
root.insert(12)
root.insert(23)
root.insert(5)
print("Postorder Traversal of Binary Search Tree: ")
root.Postorder()

Output

Postorder Traversal of Binary Search Tree: 
5
23
12
46
34
54

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild, *rightChild;
};
struct node *root = NULL;
struct node *newNode(int item){
   struct node *temp = (struct node *)malloc(sizeof(struct node));
   temp->data = item;
   temp->leftChild = temp->rightChild = NULL;
   return temp;
}
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;
            
            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
struct node* search(int data){
   struct node *current = root;
   printf("\n\nVisiting elements: ");
   while(current->data != data) {
      if(current != NULL) {
         printf("%d ",current->data);

         //go to left tree
         if(current->data > data) {
            current = current->leftChild;
         }//else go to right tree
         else {
            current = current->rightChild;
         }

         //not found
         if(current == NULL) {
            return NULL;
         }
      }
   }
   return current;
}

// Inorder Traversal
void inorder(struct node *root){
   if (root != NULL) {
      inorder(root->leftChild);
      printf("%d -> ", root->data);
      inorder(root->rightChild);
   }
}

// Preorder Traversal
void preorder(struct node *root){
   if (root != NULL) {
      printf("%d -> ", root->data);
      preorder(root->leftChild);
      preorder(root->rightChild);
   }
}

// Postorder Traversal
void postorder(struct node *root){
   if (root != NULL) {
      printf("%d -> ", root->data);
      postorder(root->leftChild);
      postorder(root->rightChild);
   }
}
int main(){
   insert(55);
   insert(20);
   insert(90);
   insert(50);
   insert(35);
   insert(15);
   insert(65);
   printf("Insertion done\n");
   printf("\nPreorder Traversal: ");
   preorder(root);
   printf("\nInorder Traversal: ");
   inorder(root);
   printf("\nPostorder Traversal: ");
   postorder(root);
   struct node* k;
   k = search(35);
   if(k != NULL)
      printf("\nElement %d found", k->data);
   else
      printf("\nElement not found");
   return 0;
}

Output

Insertion done

Preorder Traversal: 55 -> 20 -> 15 -> 50 -> 35 -> 90 -> 65 -> 
Inorder Traversal: 15 -> 20 -> 35 -> 50 -> 55 -> 65 -> 90 -> 
Postorder Traversal: 55 -> 20 -> 15 -> 50 -> 35 -> 90 -> 65 -> 

Visiting elements: 55 20 50 
Element 35 found

#include <iostream>
struct node {
   int data;
   struct node *leftChild, *rightChild;
};
struct node *root = NULL;
struct node *newNode(int item){
   struct node *temp = (struct node *)malloc(sizeof(struct node));
   temp->data = item;
   temp->leftChild = temp->rightChild = NULL;
   return temp;
}
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;
   
   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;
            
            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
struct node* search(int data){
   struct node *current = root;
   printf("\n\nVisiting elements: ");
   while(current->data != data) {
      if(current != NULL) {
         printf("%d ",current->data);
         
         //go to left tree
         if(current->data > data) {
            current = current->leftChild;
         }//else go to right tree
         else {
            current = current->rightChild;
         }
         
         //not found
         if(current == NULL) {
            return NULL;
         }
      }
   }
   return current;
}

// Inorder Traversal
void inorder(struct node *root){
   if (root != NULL) {
      inorder(root->leftChild);
      printf("%d -> ", root->data);
      inorder(root->rightChild);
   }
}

// Preorder Traversal
void preorder(struct node *root){
   if (root != NULL) {
      printf("%d -> ", root->data);
      preorder(root->leftChild);
      preorder(root->rightChild);
   }
}

// Postorder Traversal
void postorder(struct node *root){
   if (root != NULL) {
      printf("%d -> ", root->data);
      postorder(root->leftChild);
      postorder(root->rightChild);
   }
}
int main(){
   insert(55);
   insert(20);
   insert(90);
   insert(50);
   insert(35);
   insert(15);
   insert(65);
   printf("Insertion done\n");
   printf("\nPreorder Traversal: ");
   preorder(root);
   printf("\nInorder Traversal: ");
   inorder(root);
   printf("\nPostorder Traversal: ");
   postorder(root);
   struct node* k;
   k = search(35);
   if(k != NULL)
      printf("\nElement %d found", k->data);
   else
      printf("\nElement not found");
   return 0;
}

Output

Insertion done

Preorder Traversal: 55 -> 20 -> 15 -> 50 -> 35 -> 90 -> 65 -> 
Inorder Traversal: 15 -> 20 -> 35 -> 50 -> 55 -> 65 -> 90 -> 
Postorder Traversal: 55 -> 20 -> 15 -> 50 -> 35 -> 90 -> 65 -> 

Visiting elements: 55 20 50 
Element 35 found

import java.util.Scanner;
class BSTNode {
   BSTNode left, right;
   int data;
   public BSTNode(int n) {
      left = null;
      right = null;
      data = n;
   }
}
public class BST {
   static BSTNode root;
   public BST() {
      root = null;
   }
   public boolean isEmpty() {
      return root == null;
   }
   private BSTNode insert(BSTNode node, int data) {
      if(node == null)
         node = new BSTNode(data);
      else {
         if(data <= node.data)
            node.left = insert(node.left, data);
         else
            node.right = insert(node.right, data);
      }
      return node;
   }
   public void delete(int k) {
      if(isEmpty ())
         System.out.println("TREE EMPTY");
      else if(search (k) == false)
         System.out.println("SORRY " + k + " IS NOT PRESENT");
      else {
         root=delete(root,k);
         System.out.println(k + " DELETED FROM THE TREE");
      }
   }
   public BSTNode delete(BSTNode root, int k) {
      BSTNode p, p2, n;
      if(root.data == k) {
         BSTNode lt, rt;
         lt = root.left;
         rt = root.right;
         if(lt == null && rt == null) {
            return null;
         } else if(lt == null) {
            p = rt;
            return p;
         } else if(rt == null) {
            p = lt;
            return p;
         } else {
            p2 = rt;
            p = rt;
            while(p.left != null)
               p = p.left;
            p.left = lt;
            return p2;
         }
      }
      if (k < root.data) {
         n = delete(root.left, k);
         root.left = n;
      } else {
         n = delete(root.right, k);
         root.right = n;
      }
      return root;
   }
   public boolean search(int val) {
      return search(root, val);
   }
   private boolean search(BSTNode r, int val) {
      boolean found = false;
      while ((r != null) && !found) {
         int rval = r.data;
         if(val < rval)
            r = r.left;
         else if (val > rval)
            r = r.right;
         else {
            found = true;
            break;
         }
         found = search(r, val);
      }
      return found;
   }
   void printTree(BSTNode node, String prefix) {
      if(node == null)
         return;
      printTree(node.left , " " + prefix);
      System.out.println(prefix + "--" + node.data);
      printTree(node.right , prefix + " ");
   }
   public static void main(String args[]) {
      Scanner sc = new Scanner(System.in);
      BST bst = new BST();
      root = bst.insert(root, 55);
      root = bst.insert(root, 20);
      root = bst.insert(root, 90);
      root = bst.insert(root, 80);
      root = bst.insert(root, 50);
      root = bst.insert(root, 35);
      root = bst.insert(root, 15);
      root = bst.insert(root, 65);
      bst.printTree(root, " ");
      bst.delete(55);
      System.out.println("Element found = " + bst.search(80));
      System.out.println("Is Tree Empty? " + bst.isEmpty());
   }
}

Output

--15
  --20--35
   --50
 --55
    --65
   --80
  --90
55 DELETED FROM THE TREE
Element found = true
Is Tree Empty? false

class Node:
   def __init__(self, data):
     self.left = None
     self.right = None
     self.data = data

# Insert method to create nodes
   def insert(self, data):
     if self.data:
       if data < self.data:
         if self.left is None:
            self.left = Node(data)
         else:
            self.left.insert(data)
       elif data > self.data:
         if self.right is None:
            self.right = Node(data)
         else:
            self.right.insert(data)
       else:
         self.data = data

# search method to compare the value with nodes
   def search(self, key):
     if key < self.data:
       if self.left is None:
         return str(key)+" Not Found"
       return self.left.search(key)
     elif key > self.data:
       if self.right is None:
         return str(key)+" Not Found"
       return self.right.search(key)
     else:
       print(str(self.data) + ' is found')

# Print the tree
   def Inorder(self):
     if self.left:
       self.left.Inorder()
     print(self.data)
     if self.right:
       self.right.Inorder()

# Print the tree
   def Preorder(self):
     print(self.data)
     if self.left:
       self.left.Preorder()
     if self.right:
       self.right.Preorder()

# Print the tree
   def Postorder(self):
     if self.left:
       self.left.Postorder()
     if self.right:
       self.right.Postorder()
     print(self.data)

root = Node(54)
root.insert(34)
root.insert(46)
root.insert(12)
root.insert(23)
root.insert(5)
print("Preorder Traversal of Binary Search Tree: ")
root.Preorder()
print("Inorder Traversal of Binary Search Tree: ")
root.Inorder()
print("Postorder Traversal of Binary Search Tree: ")
root.Postorder()
print(root.search(17))
print(root.search(12))

Output

Preorder Traversal of Binary Search Tree: 
54
34
12
5
23
46
Inorder Traversal of Binary Search Tree: 
5
12
23
34
46
54
Postorder Traversal of Binary Search Tree: 
5
23
12
46
34
54
17 Not Found
12 is found
None

Data Structure and Algorithms - AVL Trees

The first type of self-balancing binary search tree to be invented is the AVL tree. The name AVL tree is coined after its inventor's names − Adelson-Velsky and Landis.

In AVL trees, the difference between the heights of left and right subtrees, known as the Balance Factor, must be at most one. Once the difference exceeds one, the tree automatically executes the balancing algorithm until the difference becomes one again.

BALANCE FACTOR = HEIGHT(LEFT SUBTREE) – HEIGHT(RIGHT SUBTREE)

There are usually four cases of rotation in the balancing algorithm of AVL trees: LL, RR, LR, RL.

LL Rotations

LL rotation is performed when the node is inserted into the right subtree leading to an unbalanced tree. This is a single left rotation to make the tree balanced again −

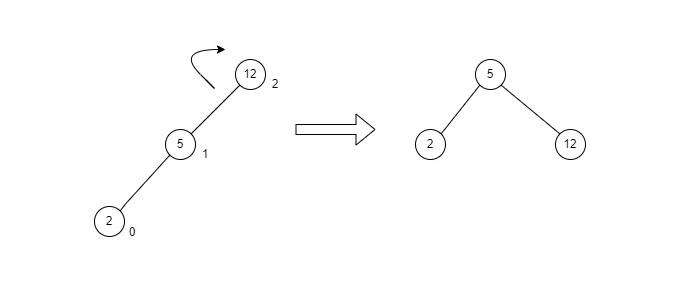
Fig : LL Rotation

The node where the unbalance occurs becomes the left child and the newly added node becomes the right child with the middle node as the parent node.

RR Rotations

RR rotation is performed when the node is inserted into the left subtree leading to an unbalanced tree. This is a single right rotation to make the tree balanced again −

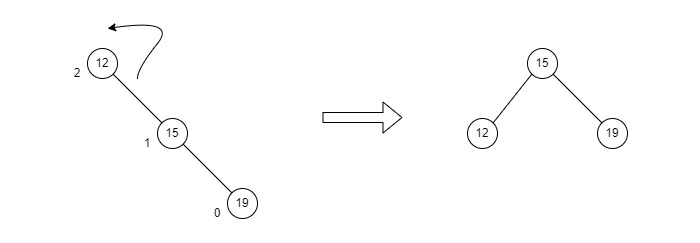
Fig : RR Rotation

The node where the unbalance occurs becomes the right child and the newly added node becomes the left child with the middle node as the parent node.

LR Rotations

LR rotation is the extended version of the previous single rotations, also called a double rotation. It is performed when a node is inserted into the right subtree of the left subtree. The LR rotation is a combination of the left rotation followed by the right rotation. There are multiple steps to be followed to carry this out.

Consider an example with “A” as the root node, “B” as the left child of “A” and “C” as the right child of “B”.
Since the unbalance occurs at A, a left rotation is applied on the child nodes of A, i.e. B and C.
After the rotation, the C node becomes the left child of A and B becomes the left child of C.
The unbalance still persists, therefore a right rotation is applied at the root node A and the left child C.
After the final right rotation, C becomes the root node, A becomes the right child and B is the left child.

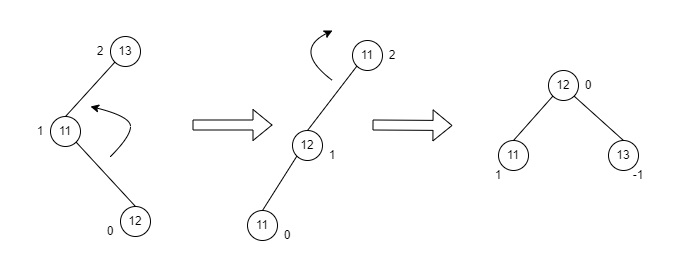
Fig : LR Rotation

RL Rotations

RL rotation is also the extended version of the previous single rotations, hence it is called a double rotation and it is performed if a node is inserted into the left subtree of the right subtree. The RL rotation is a combination of the right rotation followed by the left rotation. There are multiple steps to be followed to carry this out.

Consider an example with “A” as the root node, “B” as the right child of “A” and “C” as the left child of “B”.
Since the unbalance occurs at A, a right rotation is applied on the child nodes of A, i.e. B and C.
After the rotation, the C node becomes the right child of A and B becomes the right child of C.
The unbalance still persists, therefore a left rotation is applied at the root node A and the right child C.
After the final left rotation, C becomes the root node, A becomes the left child and B is the right child.

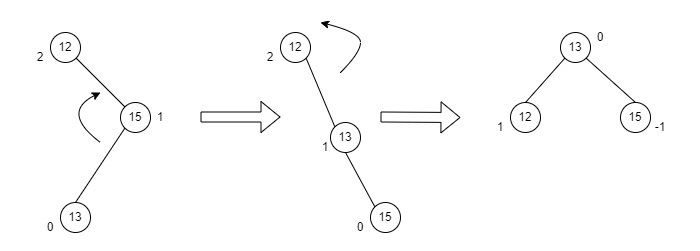
Fig : RL Rotation

Basic Operations of AVL Trees

The basic operations performed on the AVL Tree structures include all the operations performed on a binary search tree, since the AVL Tree at its core is actually just a binary search tree holding all its properties. Therefore, basic operations performed on an AVL Tree are − Insertion and Deletion.

Insertion

The data is inserted into the AVL Tree by following the Binary Search Tree property of insertion, i.e. the left subtree must contain elements less than the root value and right subtree must contain all the greater elements. However, in AVL Trees, after the insertion of each element, the balance factor of the tree is checked; if it does not exceed 1, the tree is left as it is. But if the balance factor exceeds 1, a balancing algorithm is applied to readjust the tree such that balance factor becomes less than or equal to 1 again.

Algorithm

The following steps are involved in performing the insertion operation of an AVL Tree −

Step 1 − Create a node

Step 2 − Check if the tree is empty

Step 3 − If the tree is empty, the new node created will become the root node of the AVL Tree.

Step 4 − If the tree is not empty, we perform the Binary Search Tree insertion operation and check the balancing factor of the node in the tree.

Step 5 − Suppose the balancing factor exceeds ±1, we apply suitable rotations on the said node and resume the insertion from Step 4.

START
   if node == null then:
      return new node
   if key < node.key then:
      node.left = insert (node.left, key)
   else if (key > node.key) then:
      node.right = insert (node.right, key)
   else
      return node
   node.height = 1 + max (height (node.left), height (node.right))
   balance = getBalance (node)
   if balance > 1 and key < node.left.key then:
      rightRotate
   if balance < -1 and key > node.right.key then:
      leftRotate
   if balance > 1 and key > node.left.key then:
      node.left = leftRotate (node.left)
      rightRotate
   if balance < -1 and key < node.right.key then:
      node.right = rightRotate (node.right)
      leftRotate (node)
   return node
END

Insertion Example

Let us understand the insertion operation by constructing an example AVL tree with 1 to 7 integers.

Starting with the first element 1, we create a node and measure the balance, i.e., 0.

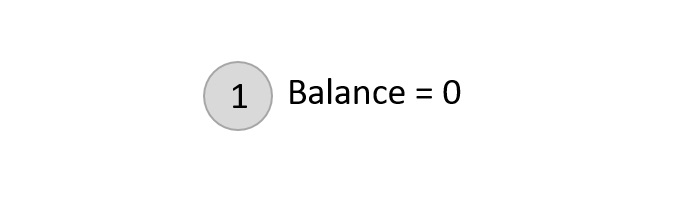
Since both the binary search property and the balance factor are satisfied, we insert another element into the tree.

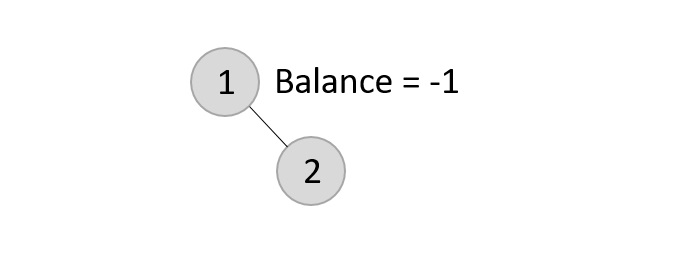
The balance factor for the two nodes are calculated and is found to be -1 (Height of left subtree is 0 and height of the right subtree is 1). Since it does not exceed 1, we add another element to the tree.

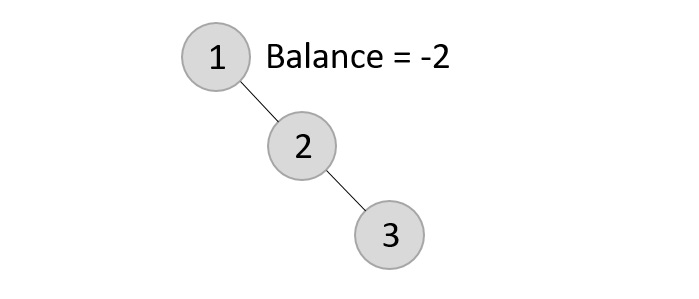
Now, after adding the third element, the balance factor exceeds 1 and becomes 2. Therefore, rotations are applied. In this case, the RR rotation is applied since the imbalance occurs at two right nodes.

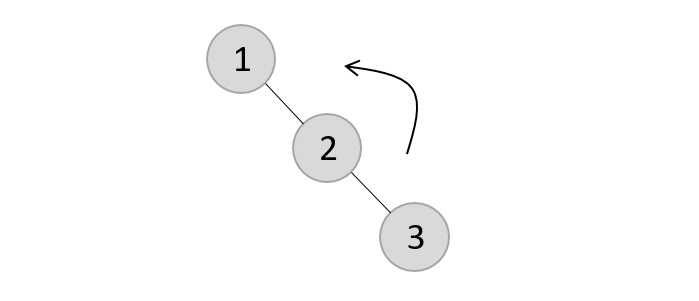
The tree is rearranged as −

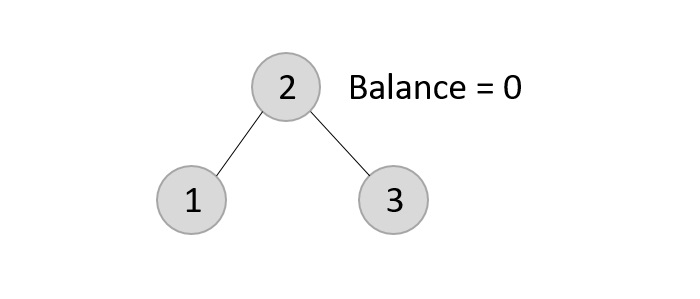
Similarly, the next elements are inserted and rearranged using these rotations. After rearrangement, we achieve the tree as −

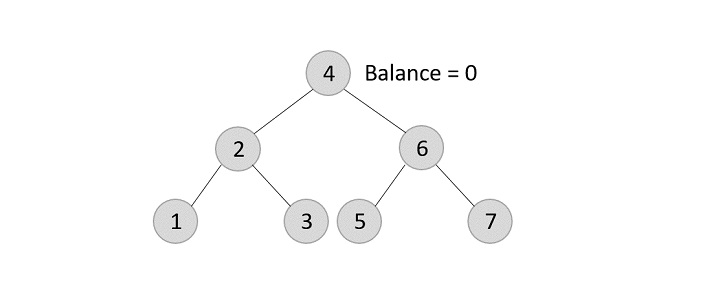
Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
#include <stdlib.h>
struct Node {
   int data;
   struct Node *leftChild;
   struct Node *rightChild;
   int height;
};
int max(int a, int b);
int height(struct Node *N){
   if (N == NULL)
      return 0;
   return N->height;
}
int max(int a, int b){
   return (a > b) ? a : b;
}
struct Node *newNode(int data){
   struct Node *node = (struct Node *) malloc(sizeof(struct Node));
   node->data = data;
   node->leftChild = NULL;
   node->rightChild = NULL;
   node->height = 1;
   return (node);
}
struct Node *rightRotate(struct Node *y){
   struct Node *x = y->leftChild;
   struct Node *T2 = x->rightChild;
   x->rightChild = y;
   y->leftChild = T2;
   y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
   x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
   return x;
}
struct Node *leftRotate(struct Node *x){
   struct Node *y = x->rightChild;
   struct Node *T2 = y->leftChild;
   y->leftChild = x;
   x->rightChild = T2;
   x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
   y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
   return y;
}
int getBalance(struct Node *N){
   if (N == NULL)
      return 0;
   return height(N->leftChild) - height(N->rightChild);
}
struct Node *insertNode(struct Node *node, int data){
   if (node == NULL)
      return (newNode(data));
   if (data < node->data)
      node->leftChild = insertNode(node->leftChild, data);
   else if (data > node->data)
      node->rightChild = insertNode(node->rightChild, data);
   else
      return node;
   node->height = 1 + max(height(node->leftChild),
                     height(node->rightChild));
   int balance = getBalance(node);
   if (balance > 1 && data < node->leftChild->data)
      return rightRotate(node);
   if (balance < -1 && data > node->rightChild->data)
      return leftRotate(node);
   if (balance > 1 && data > node->leftChild->data) {
      node->leftChild = leftRotate(node->leftChild);
      return rightRotate(node);
   }
   if (balance < -1 && data < node->rightChild->data) {
      node->rightChild = rightRotate(node->rightChild);
      return leftRotate(node);
   }
   return node;
}
struct Node *minValueNode(struct Node *node){
   struct Node *current = node;
   while (current->leftChild != NULL)
      current = current->leftChild;
   return current;
}
void printTree(struct Node *root){
   if (root == NULL)
      return;
   if (root != NULL) {
      printTree(root->leftChild);
      printf("%d ", root->data);
      printTree(root->rightChild);
   }
}
int main(){
   struct Node *root = NULL;
   root = insertNode(root, 22);
   root = insertNode(root, 14);
   root = insertNode(root, 72);
   root = insertNode(root, 44);
   root = insertNode(root, 25);
   root = insertNode(root, 63);
   root = insertNode(root, 98);
   printf("AVL Tree: ");
   printTree(root);
   return 0;
}

Output

AVL Tree: 14 22 25 44 63 72 98

#include <iostream>
struct Node {
   int data;
   struct Node *leftChild;
   struct Node *rightChild;
   int height;
};
int max(int a, int b);
int height(struct Node *N){
   if (N == NULL)
      return 0;
   return N->height;
}
int max(int a, int b){
   return (a > b) ? a : b;
}
struct Node *newNode(int data){
   struct Node *node = (struct Node *) malloc(sizeof(struct Node));
   node->data = data;
   node->leftChild = NULL;
   node->rightChild = NULL;
   node->height = 1;
   return (node);
}
struct Node *rightRotate(struct Node *y){
   struct Node *x = y->leftChild;
   struct Node *T2 = x->rightChild;
   x->rightChild = y;
   y->leftChild = T2;
   y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
   x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
   return x;
}
struct Node *leftRotate(struct Node *x){
   struct Node *y = x->rightChild;
   struct Node *T2 = y->leftChild;
   y->leftChild = x;
   x->rightChild = T2;
   x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
   y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
   return y;
}
int getBalance(struct Node *N){
   if (N == NULL)
      return 0;
   return height(N->leftChild) - height(N->rightChild);
}
struct Node *insertNode(struct Node *node, int data){
   if (node == NULL)
      return (newNode(data));
   if (data < node->data)
      node->leftChild = insertNode(node->leftChild, data);
   else if (data > node->data)
      node->rightChild = insertNode(node->rightChild, data);
   else
      return node;
   node->height = 1 + max(height(node->leftChild),
                     height(node->rightChild));
   int balance = getBalance(node);
   if (balance > 1 && data < node->leftChild->data)
      return rightRotate(node);
   if (balance < -1 && data > node->rightChild->data)
      return leftRotate(node);
   if (balance > 1 && data > node->leftChild->data) {
      node->leftChild = leftRotate(node->leftChild);
      return rightRotate(node);
   }
   if (balance < -1 && data < node->rightChild->data) {
      node->rightChild = rightRotate(node->rightChild);
      return leftRotate(node);
   }
   return node;
}
struct Node *minValueNode(struct Node *node){
   struct Node *current = node;
   while (current->leftChild != NULL)
      current = current->leftChild;
   return current;
}
void printTree(struct Node *root){
   if (root == NULL)
      return;
   if (root != NULL) {
      printTree(root->leftChild);
      printf("%d ", root->data);
      printTree(root->leftChild);
   }
}
int main(){
   struct Node *root = NULL;
   root = insertNode(root, 22);
   root = insertNode(root, 14);
   root = insertNode(root, 72);
   root = insertNode(root, 44);
   root = insertNode(root, 25);
   root = insertNode(root, 63);
   root = insertNode(root, 98);
   printf("AVL Tree: ");
   printTree(root);
   return 0;
}

Output

AVL Tree: 14 22 14 44 14 22 14

import java.util.*;
import java.io.*;
class Node {
   int key, height;
   Node left, right;
   Node (int d) {
      key = d;
      height = 1;
   }
}
public class AVLTree {
   Node root;
   int height (Node N) {
      if (N == null)
         return 0;
      return N.height;
   }
   int max (int a, int b) {
      return (a > b) ? a : b;
   }
   Node rightRotate (Node y) {
      Node x = y.left;
      Node T2 = x.right;
      x.right = y;
      y.left = T2;
      y.height = max (height (y.left), height (y.right)) + 1;
      x.height = max (height (x.left), height (x.right)) + 1;
      return x;
   }
   Node leftRotate (Node x) {
      Node y = x.right;
      Node T2 = y.left;
      y.left = x;
      x.right = T2;
      x.height = max (height (x.left), height (x.right)) + 1;
      y.height = max (height (y.left), height (y.right)) + 1;
      return y;
   }
   int getBalance (Node N) {
      if (N == null)
         return 0;
      return height (N.left) - height (N.right);
   }
   Node insert (Node node, int key) {
      if (node == null)
         return (new Node (key));
      if (key < node.key)
         node.left = insert (node.left, key);
      else if (key > node.key)
         node.right = insert (node.right, key);
      else
         return node;
      node.height = 1 + max (height (node.left), height (node.right));
      int balance = getBalance (node);
      if (balance > 1 && key < node.left.key)
         return rightRotate (node);
      if (balance < -1 && key > node.right.key)
         return leftRotate (node);
      if (balance > 1 && key > node.left.key) {
         node.left = leftRotate (node.left);
         return rightRotate (node);
      }
      if (balance < -1 && key < node.right.key) {
         node.right = rightRotate (node.right);
         return leftRotate (node);
      }
      return node;
   }
   void printTree(Node root){
   if (root == null)
      return;
   if (root != null) {
      printTree(root.left);
      System.out.print(root.key + " ");
      printTree(root.left);
   }
}
   public static void main(String args[]) {
      AVLTree tree = new AVLTree();

      tree.root = tree.insert(tree.root, 10); 
      tree.root = tree.insert(tree.root, 11); 
      tree.root = tree.insert(tree.root, 12); 
      tree.root = tree.insert(tree.root, 13); 
      tree.root = tree.insert(tree.root, 14); 
      tree.root = tree.insert(tree.root, 15); 
      System.out.println("AVL Tree: ");
      tree.printTree(tree.root);

   }
}

Output

AVL Tree: 
10 11 10 13 10 11 10

class Node(object):
   def __init__(self, data):
      self.data = data
      self.left = None
      self.right = None
      self.height = 1
class AVLTree(object):
   def insert(self, root, key):
      if not root:
         return Node(key)
      elif key < root.data:
         root.left = self.insert(root.left, key)
      else:
         root.right = self.insert(root.right, key)
      root.h = 1 + max(self.getHeight(root.left),
         self.getHeight(root.right))
      b = self.getBalance(root)
      if b > 1 and key < root.left.data:
         return self.rightRotate(root)
      if b < -1 and key > root.right.data:
         return self.leftRotate(root)
      if b > 1 and key > root.left.data:
         root.left = self.lefttRotate(root.left)
         return self.rightRotate(root)
      if b < -1 and key < root.right.data:
         root.right = self.rightRotate(root.right)
         return self.leftRotate(root)
      return root
   def leftRotate(self, z):
      y = z.right
      T2 = y.left
      y.left = z
      z.right = T2
      z.height = 1 + max(self.getHeight(z.left),
         self.getHeight(z.right))
      y.height = 1 + max(self.getHeight(y.left),
         self.getHeight(y.right))
      return y
   def rightRotate(self, z):
      y = z.left
      T3 = y.right
      y.right = z
      z.left = T3
      z.height = 1 + max(self.getHeight(z.left),
         self.getHeight(z.right))
      y.height = 1 + max(self.getHeight(y.left),
         self.getHeight(y.right))
      return y
   def getHeight(self, root):
      if not root:
         return 0
      return root.height
   def getBalance(self, root):
      if not root:
         return 0
      return self.getHeight(root.left) - self.getHeight(root.right)
   def Inorder(self, root):
      if root.left:
         self.Inorder(root.left)
      print(root.data)
      if root.right:
         self.Inorder(root.right)
Tree = AVLTree()
root = None

root = Tree.insert(root, 10)
root = Tree.insert(root, 13)
root = Tree.insert(root, 11)
root = Tree.insert(root, 14)
root = Tree.insert(root, 12)
root = Tree.insert(root, 15)

# Inorder Traversal
print("Inorder traversal of the AVL tree is")
Tree.Inorder(root)

Output

Inorder traversal of the AVL tree is
10
11
12
13
14
15

Deletion

Deletion in the AVL Trees take place in three different scenarios −

Scenario 1 (Deletion of a leaf node) − If the node to be deleted is a leaf node, then it is deleted without any replacement as it does not disturb the binary search tree property. However, the balance factor may get disturbed, so rotations are applied to restore it.
Scenario 2 (Deletion of a node with one child) − If the node to be deleted has one child, replace the value in that node with the value in its child node. Then delete the child node. If the balance factor is disturbed, rotations are applied.
Scenario 3 (Deletion of a node with two child nodes) − If the node to be deleted has two child nodes, find the inorder successor of that node and replace its value with the inorder successor value. Then try to delete the inorder successor node. If the balance factor exceeds 1 after deletion, apply balance algorithms.

START
   if root == null: return root
   if key < root.key:
      root.left = delete Node
   else if key > root.key:
      root.right = delete Node
   else:
      if root.left == null or root.right == null then:
         Node temp = null
         if (temp == root.left)
            temp = root.right
         else
            temp = root.left
         if temp == null then:
            temp = root
            root = null
         else
            root = temp
         else:
            temp = minimum valued node
            root.key = temp.key
            root.right = delete Node
      if (root == null) then:
         return root
         root.height = max (height (root.left), height (root.right)) + 1
         balance = getBalance
      if balance > 1 and getBalance (root.left) >= 0:
         rightRotate
      if balance > 1 and getBalance (root.left) < 0:
         root.left = leftRotate (root.left);
         rightRotate
      if balance < -1 and getBalance (root.right) <= 0:
         leftRotate
      if balance < -1 and getBalance (root.right) > 0:
         root.right = rightRotate (root.right);
         leftRotate
      return root
END

Deletion Example

Using the same tree given above, let us perform deletion in three scenarios −

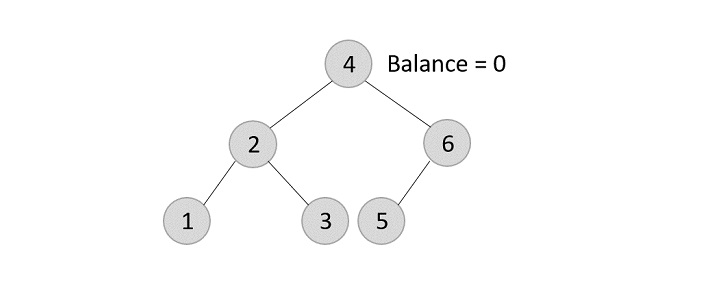
Deleting element 7 from the tree above −

Since the element 7 is a leaf, we normally remove the element without disturbing any other node in the tree

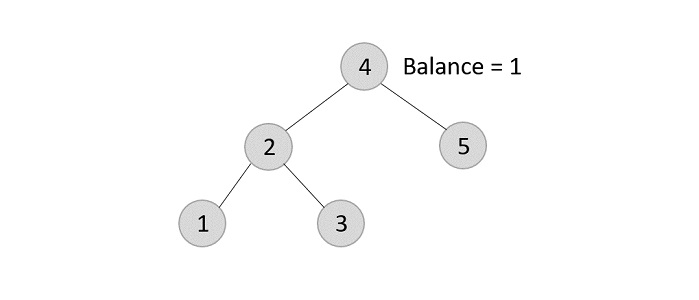
Deleting element 6 from the output tree achieved −

However, element 6 is not a leaf node and has one child node attached to it. In this case, we replace node 6 with its child node: node 5.

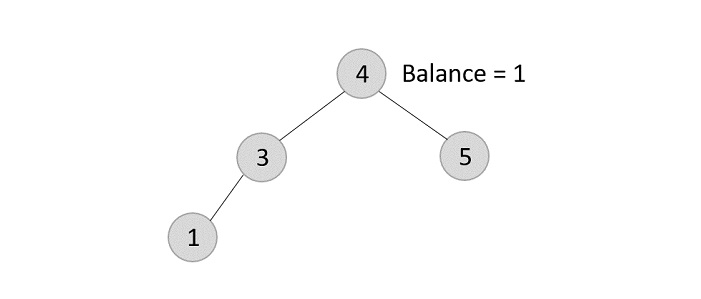
The balance of the tree becomes 1, and since it does not exceed 1 the tree is left as it is. If we delete the element 5 further, we would have to apply the left rotations; either LL or LR since the imbalance occurs at both 1-2-4 and 3-2-4.

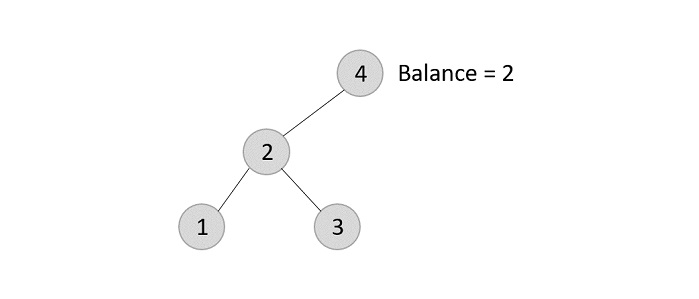
The balance factor is disturbed after deleting the element 5, therefore we apply LL rotation (we can also apply the LR rotation here).

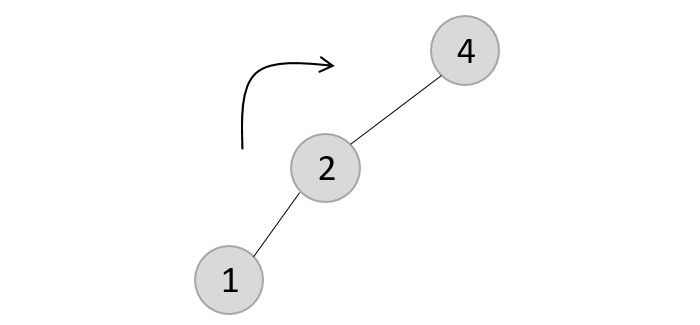
Once the LL rotation is applied on path 1-2-4, the node 3 remains as it was supposed to be the right child of node 2 (which is now occupied by node 4). Hence, the node is added to the right subtree of the node 2 and as the left child of the node 4.

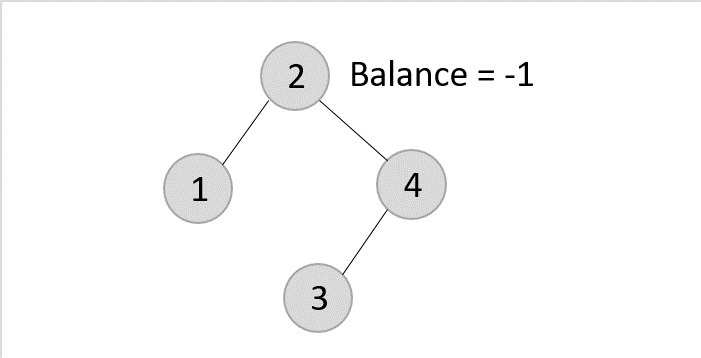
Deleting element 2 from the remaining tree −

As mentioned in scenario 3, this node has two children. Therefore, we find its inorder successor that is a leaf node (say, 3) and replace its value with the inorder successor.

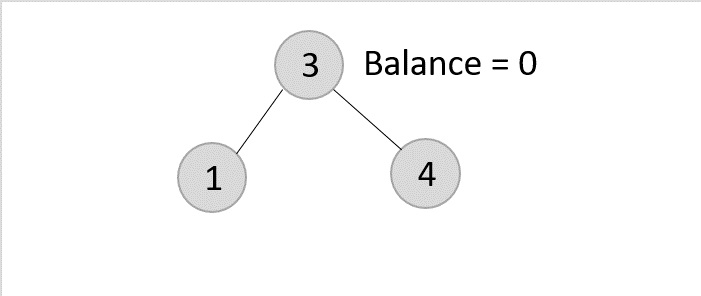
The balance of the tree still remains 1, therefore we leave the tree as it is without performing any rotations.

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
#include <stdlib.h>
struct Node {
   int data;
   struct Node *leftChild;
   struct Node *rightChild;
   int height;
};
int max(int a, int b);
int height(struct Node *N){
   if (N == NULL)
      return 0;
   return N->height;
}
int max(int a, int b){
   return (a > b) ? a : b;
}
struct Node *newNode(int data){
   struct Node *node = (struct Node *) malloc(sizeof(struct Node));
   node->data = data;
   node->leftChild = NULL;
   node->rightChild = NULL;
   node->height = 1;
   return (node);
}
struct Node *rightRotate(struct Node *y){
   struct Node *x = y->leftChild;
   struct Node *T2 = x->rightChild;
   x->rightChild = y;
   y->leftChild = T2;
   y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
   x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
   return x;
}
struct Node *leftRotate(struct Node *x){
   struct Node *y = x->rightChild;
   struct Node *T2 = y->leftChild;
   y->leftChild = x;
   x->rightChild = T2;
   x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
   y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
   return y;
}
int getBalance(struct Node *N){
   if (N == NULL)
      return 0;
   return height(N->leftChild) - height(N->rightChild);
}
struct Node *insertNode(struct Node *node, int data){
   if (node == NULL)
      return (newNode(data));
   if (data < node->data)
      node->leftChild = insertNode(node->leftChild, data);
   else if (data > node->data)
      node->rightChild = insertNode(node->rightChild, data);
   else
      return node;
   node->height = 1 + max(height(node->leftChild),
                     height(node->rightChild));
   int balance = getBalance(node);
   if (balance > 1 && data < node->leftChild->data)
      return rightRotate(node);
   if (balance < -1 && data > node->rightChild->data)
      return leftRotate(node);
   if (balance > 1 && data > node->leftChild->data) {
      node->leftChild = leftRotate(node->leftChild);
      return rightRotate(node);
   }
   if (balance < -1 && data < node->rightChild->data) {
      node->rightChild = rightRotate(node->rightChild);
      return leftRotate(node);
   }
   return node;
}
struct Node *minValueNode(struct Node *node){
   struct Node *current = node;
   while (current->leftChild != NULL)
      current = current->leftChild;
   return current;
}
struct Node *deleteNode(struct Node *root, int data){
   if (root == NULL)
      return root;
   if (data < root->data)
      root->leftChild = deleteNode(root->leftChild, data);
   else if (data > root->data)
      root->rightChild = deleteNode(root->rightChild, data);
   else {
      if ((root->leftChild == NULL) || (root->rightChild == NULL)) {
         struct Node *temp = root->leftChild ? root->leftChild : root->rightChild;
         if (temp == NULL) {
            temp = root;
            root = NULL;
         } else
            *root = *temp;
         free(temp);
      } else {
         struct Node *temp = minValueNode(root->rightChild);
         root->data = temp->data;
         root->rightChild = deleteNode(root->rightChild, temp->data);
      }
   }
   if (root == NULL)
      return root;
   root->height = 1 + max(height(root->leftChild),
                     height(root->rightChild));
   int balance = getBalance(root);
   if (balance > 1 && getBalance(root->leftChild) >= 0)
      return rightRotate(root);
   if (balance > 1 && getBalance(root->leftChild) < 0) {
      root->leftChild = leftRotate(root->leftChild);
      return rightRotate(root);
   }
   if (balance < -1 && getBalance(root->rightChild) <= 0)
      return leftRotate(root);
   if (balance < -1 && getBalance(root->rightChild) > 0) {
      root->rightChild = rightRotate(root->rightChild);
      return leftRotate(root);
   }
   return root;
}

// Print the tree
void printTree(struct Node *root){
   if (root != NULL) {
      printTree(root->leftChild);
      printf("%d ", root->data);
      printTree(root->rightChild);
   }
}
int main(){
   struct Node *root = NULL;
   root = insertNode(root, 22);
   root = insertNode(root, 14);
   root = insertNode(root, 72);
   root = insertNode(root, 44);
   root = insertNode(root, 25);
   root = insertNode(root, 63);
   root = insertNode(root, 98);
   printf("AVL Tree: ");
   printTree(root);
   root = deleteNode(root, 25);
   printf("\nAfter deletion: ");
   printTree(root);
   return 0;
}

Output

AVL Tree: 14 22 25 44 63 72 98 
After deletion: 14 22 44 63 72 98

#include <iostream>
struct Node {
   int data;
   struct Node *leftChild;
   struct Node *rightChild;
   int height;
};
int max(int a, int b);
int height(struct Node *N){
   if (N == NULL)
      return 0;
   return N->height;
}
int max(int a, int b){
   return (a > b) ? a : b;
}
struct Node *newNode(int data){
   struct Node *node = (struct Node *) malloc(sizeof(struct Node));
   node->data = data;
   node->leftChild = NULL;
   node->rightChild = NULL;
   node->height = 1;
   return (node);
}
struct Node *rightRotate(struct Node *y){
   struct Node *x = y->leftChild;
   struct Node *T2 = x->rightChild;
   x->rightChild = y;
   y->leftChild = T2;
   y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
   x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
   return x;
}
struct Node *leftRotate(struct Node *x){
   struct Node *y = x->rightChild;
   struct Node *T2 = y->leftChild;
   y->leftChild = x;
   x->rightChild = T2;
   x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
   y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
   return y;
}
int getBalance(struct Node *N){
   if (N == NULL)
      return 0;
   return height(N->leftChild) - height(N->rightChild);
}
struct Node *insertNode(struct Node *node, int data){
   if (node == NULL)
      return (newNode(data));
   if (data < node->data)
      node->leftChild = insertNode(node->leftChild, data);
   else if (data > node->data)
      node->rightChild = insertNode(node->rightChild, data);
   else
      return node;
   node->height = 1 + max(height(node->leftChild),
                     height(node->rightChild));
   int balance = getBalance(node);
   if (balance > 1 && data < node->leftChild->data)
      return rightRotate(node);
   if (balance < -1 && data > node->rightChild->data)
      return leftRotate(node);
   if (balance > 1 && data > node->leftChild->data) {
      node->leftChild = leftRotate(node->leftChild);
      return rightRotate(node);
   }
   if (balance < -1 && data < node->rightChild->data) {
      node->rightChild = rightRotate(node->rightChild);
      return leftRotate(node);
   }
   return node;
}
struct Node *minValueNode(struct Node *node){
   struct Node *current = node;
   while (current->leftChild != NULL)
      current = current->leftChild;
   return current;
}
struct Node *deleteNode(struct Node *root, int data){
   if (root == NULL)
      return root;
   if (data < root->data)
      root->leftChild = deleteNode(root->leftChild, data);
   else if (data > root->data)
      root->rightChild = deleteNode(root->rightChild, data);
   else {
      if ((root->leftChild == NULL) || (root->rightChild == NULL)) {
         struct Node *temp = root->leftChild ? root->leftChild : root->rightChild;
         if (temp == NULL) {
            temp = root;
            root = NULL;
         } else
            *root = *temp;
         free(temp);
      } else {
         struct Node *temp = minValueNode(root->rightChild);
         root->data = temp->data;
         root->rightChild = deleteNode(root->rightChild, temp->data);
      }
   }
   if (root == NULL)
      return root;
   root->height = 1 + max(height(root->leftChild),
                     height(root->rightChild));
   int balance = getBalance(root);
   if (balance > 1 && getBalance(root->leftChild) >= 0)
      return rightRotate(root);
   if (balance > 1 && getBalance(root->leftChild) < 0) {
      root->leftChild = leftRotate(root->leftChild);
      return rightRotate(root);
   }
   if (balance < -1 && getBalance(root->rightChild) <= 0)
      return leftRotate(root);
   if (balance < -1 && getBalance(root->rightChild) > 0) {
      root->rightChild = rightRotate(root->rightChild);
      return leftRotate(root);
   }
   return root;
}

// Print the tree
void printTree(struct Node *root){
   if (root != NULL) {
      printTree(root->leftChild);
      printf("%d ", root->data);
      printTree(root->rightChild);
   }
}
int main(){
   struct Node *root = NULL;
   root = insertNode(root, 22);
   root = insertNode(root, 14);
   root = insertNode(root, 72);
   root = insertNode(root, 44);
   root = insertNode(root, 25);
   root = insertNode(root, 63);
   root = insertNode(root, 98);
   printf("AVL Tree: ");
   printTree(root);
   root = deleteNode(root, 25);
   printf("\nAfter deletion: ");
   printTree(root);
   return 0;
}

Output

AVL Tree: 14 22 25 44 63 72 98 
After deletion: 14 22 44 63 72 98

import java.util.*;
import java.io.*;
class Node {
   int key, height;
   Node left, right;
   Node (int d) {
      key = d;
      height = 1;
   }
}
public class AVLTree {
   Node root;
   int height (Node N) {
      if (N == null)
         return 0;
      return N.height;
   }
   int max (int a, int b) {
      return (a > b) ? a : b;
   }
   Node rightRotate (Node y) {
      Node x = y.left;
      Node T2 = x.right;
      x.right = y;
      y.left = T2;
      y.height = max (height (y.left), height (y.right)) + 1;
      x.height = max (height (x.left), height (x.right)) + 1;
      return x;
   }
   Node leftRotate (Node x) {
      Node y = x.right;
      Node T2 = y.left;
      y.left = x;
      x.right = T2;
      x.height = max (height (x.left), height (x.right)) + 1;
      y.height = max (height (y.left), height (y.right)) + 1;
      return y;
   }
   int getBalance (Node N) {
      if (N == null)
         return 0;
      return height (N.left) - height (N.right);
   }
   Node minValueNode (Node node) {
      Node current = node;
      while (current.left != null)
         current = current.left;
      return current;
   }
   Node deleteNode (Node root, int key) {
      if (root == null)
         return root;
      if (key < root.key)
         root.left = deleteNode (root.left, key);
      else if (key > root.key)
         root.right = deleteNode (root.right, key);
      else {
         if ((root.left == null) || (root.right == null)) {
            Node temp = null;
            if (temp == root.left)
               temp = root.right;
            else
               temp = root.left;
            if (temp == null) {
               temp = root;
               root = null;
            } else
               root = temp;
         } else {
            Node temp = minValueNode (root.right);
            root.key = temp.key;
            root.right = deleteNode (root.right, temp.key);
         }
      }
      if (root == null)
         return root;
      root.height = max (height (root.left), height (root.right)) + 1;
      int balance = getBalance (root);
      if (balance > 1 && getBalance (root.left) >= 0)
         return rightRotate (root);
      if (balance > 1 && getBalance (root.left) < 0) {
         root.left = leftRotate (root.left);
         return rightRotate (root);
      }
      if (balance < -1 && getBalance (root.right) <= 0)
         return leftRotate (root);
      if (balance < -1 && getBalance (root.right) > 0) {
         root.right = rightRotate (root.right);
         return leftRotate (root);
      }
      return root;
   }
   public void printTree(Node root) {
      if (root == null) return;
      printTree(root.left);
      System.out.print(root.key + " ");
      printTree(root.right);
   }
   public static void main (String[]args) {
      AVLTree tree = new AVLTree();
      tree.root = new Node(13);
      tree.root.left = new Node(12);
      tree.root.left.left = new Node(11);
      tree.root.left.left.left = new Node(10);
      tree.root.right = new Node(14);
      tree.root.right.right = new Node(15);
      System.out.println("The AVL Tree is: ");
      tree.printTree(tree.root);
      tree.root = tree.deleteNode (tree.root, 10);
      System.out.println("\n----------------------------------------------\n");
      System.out.println("The AVL Tree after deleting 10 is: ");
      tree.printTree(tree.root);
      System.out.println ("");
   }
}

Output

The AVL Tree is: 
10 11 12 13 14 15 
----------------------------------------------

The AVL Tree after deleting 10 is: 
11 12 13 14 15

class Node(object):
   def __init__(self, data):
      self.data = data
      self.left = None
      self.right = None
      self.height = 1
class AVLTree(object):
   def insert(self, root, key):
      if not root:
         return Node(key)
      elif key < root.data:
         root.left = self.insert(root.left, key)
      else:
         root.right = self.insert(root.right, key)
      root.h = 1 + max(self.getHeight(root.left),
         self.getHeight(root.right))
      b = self.getBalance(root)
      if b > 1 and key < root.left.data:
         return self.rightRotate(root)
      if b < -1 and key > root.right.data:
         return self.leftRotate(root)
      if b > 1 and key > root.left.data:
         root.left = self.lefttRotate(root.left)
         return self.rightRotate(root)
      if b < -1 and key < root.right.data:
          root.right = self.rightRotate(root.right)
          return self.leftRotate(root)
      return root
   def delete(self, root, key):
      if not root:
         return root
      elif key < root.data:
         root.left = self.delete(root.left, key)
      elif key > root.data:
         root.right = self.delete(root.right, key)
      else:
         if root.left is None:
            temp = root.right
            root = None
            return temp
         elif root.right is None:
            temp = root.left
            root = None
            return temp
         temp = self.getMindataueNode(root.right)
         root.data = temp.data
         root.right = self.delete(root.right, temp.data)
      if root is None:
         return root
      root.height = 1 + max(self.getHeight(root.left), self.getHeight(root.right))
      balance = self.getBalance(root)
      if balance > 1 and self.getBalance(root.left) >= 0:
         return self.rightRotate(root)
      if balance < -1 and self.getBalance(root.right) <= 0:
         return self.leftRotate(root)
      if balance > 1 and self.getBalance(root.left) < 0:
         root.left = self.leftRotate(root.left)
         return self.rightRotate(root)
      if balance < -1 and self.getBalance(root.right) > 0:
         root.right = self.rightRotate(root.right)
         return self.leftRotate(root)
      return root
   def leftRotate(self, z):
      y = z.right
      T2 = y.left
      y.left = z
      z.right = T2
      z.height = 1 + max(self.getHeight(z.left),
         self.getHeight(z.right))
      y.height = 1 + max(self.getHeight(y.left),
         self.getHeight(y.right))
      return y
   def rightRotate(self, z):
      y = z.left
      T3 = y.right
      y.right = z
      z.left = T3
      z.height = 1 + max(self.getHeight(z.left),
         self.getHeight(z.right))
      y.height = 1 + max(self.getHeight(y.left),
         self.getHeight(y.right))
      return y
   def getHeight(self, root):
      if not root:
         return 0
      return root.height
   def getBalance(self, root):
      if not root:
         return 0
      return self.getHeight(root.left) - self.getHeight(root.right)
   def Inorder(self, root):
      if root.left:
         self.Inorder(root.left)
      print(root.data)
      if root.right:
         self.Inorder(root.right)

Tree = AVLTree()
root = None
root = Tree.insert(root, 10)
root = Tree.insert(root, 13)
root = Tree.insert(root, 11)
root = Tree.insert(root, 14)
root = Tree.insert(root, 12)
root = Tree.insert(root, 15)

# Inorder Traversal
print("Inorder traversal of the AVL tree is")
Tree.Inorder(root)
root = Tree.delete(root, 14)
print("Inorder traversal of the modified AVL tree is")
Tree.Inorder(root)

Output

Inorder traversal of the AVL tree is
10
11
12
13
14
15
Inorder traversal of the modified AVL tree is
10
11
12
13
15

Implementation of AVL Trees

In the following implementation, we consider the inputs in ascending order and store them in AVL Trees by calculating the balance factor and applying rotations.

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python

#include <stdio.h>
#include <stdlib.h>
struct Node {
   int data;
   struct Node *leftChild;
   struct Node *rightChild;
   int height;
};
int max(int a, int b);
int height(struct Node *N){
   if (N == NULL)
      return 0;
   return N->height;
}
int max(int a, int b){
   return (a > b) ? a : b;
}
struct Node *newNode(int data){
   struct Node *node = (struct Node *) malloc(sizeof(struct Node));
   node->data = data;
   node->leftChild = NULL;
   node->rightChild = NULL;
   node->height = 1;
   return (node);
}
struct Node *rightRotate(struct Node *y){
   struct Node *x = y->leftChild;
   struct Node *T2 = x->rightChild;
   x->rightChild = y;
   y->leftChild = T2;
   y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
   x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
   return x;
}
struct Node *leftRotate(struct Node *x){
   struct Node *y = x->rightChild;
   struct Node *T2 = y->leftChild;
   y->leftChild = x;
   x->rightChild = T2;
   x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
   y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
   return y;
}
int getBalance(struct Node *N){
   if (N == NULL)
      return 0;
   return height(N->leftChild) - height(N->rightChild);
}
struct Node *insertNode(struct Node *node, int data){
   if (node == NULL)
      return (newNode(data));
   if (data < node->data)
      node->leftChild = insertNode(node->leftChild, data);
   else if (data > node->data)
      node->rightChild = insertNode(node->rightChild, data);
   else
      return node;
   node->height = 1 + max(height(node->leftChild),
                     height(node->rightChild));
   int balance = getBalance(node);
   if (balance > 1 && data < node->leftChild->data)
      return rightRotate(node);
   if (balance < -1 && data > node->rightChild->data)
      return leftRotate(node);
   if (balance > 1 && data > node->leftChild->data) {
      node->leftChild = leftRotate(node->leftChild);
      return rightRotate(node);
   }
   if (balance < -1 && data < node->rightChild->data) {
      node->rightChild = rightRotate(node->rightChild);
      return leftRotate(node);
   }
   return node;
}
struct Node *minValueNode(struct Node *node){
   struct Node *current = node;
   while (current->leftChild != NULL)
      current = current->leftChild;
   return current;
}
struct Node *deleteNode(struct Node *root, int data){
   if (root == NULL)
      return root;
   if (data < root->data)
      root->leftChild = deleteNode(root->leftChild, data);
   else if (data > root->data)
      root->rightChild = deleteNode(root->rightChild, data);
   else {
      if ((root->leftChild == NULL) || (root->rightChild == NULL)) {
         struct Node *temp = root->leftChild ? root->leftChild : root->rightChild;
         if (temp == NULL) {
            temp = root;
            root = NULL;
         } else
            *root = *temp;
         free(temp);
      } else {
         struct Node *temp = minValueNode(root->rightChild);
         root->data = temp->data;
         root->rightChild = deleteNode(root->rightChild, temp->data);
      }
   }
   if (root == NULL)
      return root;
   root->height = 1 + max(height(root->leftChild),
                     height(root->rightChild));
   int balance = getBalance(root);
   if (balance > 1 && getBalance(root->leftChild) >= 0)
      return rightRotate(root);
   if (balance > 1 && getBalance(root->leftChild) < 0) {
      root->leftChild = leftRotate(root->leftChild);
      return rightRotate(root);
   }
   if (balance < -1 && getBalance(root->rightChild) <= 0)
      return leftRotate(root);
   if (balance < -1 && getBalance(root->rightChild) > 0) {
      root->rightChild = rightRotate(root->rightChild);
      return leftRotate(root);
   }
   return root;
}

// Print the tree
void printTree(struct Node *root){
   if (root != NULL) {
      printTree(root->leftChild);
      printf("%d ", root->data);
      printTree(root->rightChild);
   }
}
int main(){
   struct Node *root = NULL;
   root = insertNode(root, 22);
   root = insertNode(root, 14);
   root = insertNode(root, 72);
   root = insertNode(root, 44);
   root = insertNode(root, 25);
   root = insertNode(root, 63);
   root = insertNode(root, 98);
   printf("AVL Tree: ");
   printTree(root);
   root = deleteNode(root, 25);
   printf("\nAfter deletion: ");
   printTree(root);
   return 0;
}

Output

AVL Tree: 14 22 25 44 63 72 98 
After deletion: 14 22 44 63 72 98

#include <iostream>
struct Node {
   int data;
   struct Node *leftChild;
   struct Node *rightChild;
   int height;
};
int max(int a, int b);
int height(struct Node *N){
   if (N == NULL)
      return 0;
   return N->height;
}
int max(int a, int b){
   return (a > b) ? a : b;
}
struct Node *newNode(int data){
   struct Node *node = (struct Node *) malloc(sizeof(struct Node));
   node->data = data;
   node->leftChild = NULL;
   node->rightChild = NULL;
   node->height = 1;
   return (node);
}
struct Node *rightRotate(struct Node *y){
   struct Node *x = y->leftChild;
   struct Node *T2 = x->rightChild;
   x->rightChild = y;
   y->leftChild = T2;
   y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
   x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
   return x;
}
struct Node *leftRotate(struct Node *x){
   struct Node *y = x->rightChild;
   struct Node *T2 = y->leftChild;
   y->leftChild = x;
   x->rightChild = T2;
   x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
   y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
   return y;
}
int getBalance(struct Node *N){
   if (N == NULL)
      return 0;
   return height(N->leftChild) - height(N->rightChild);
}
struct Node *insertNode(struct Node *node, int data){
   if (node == NULL)
      return (newNode(data));
   if (data < node->data)
      node->leftChild = insertNode(node->leftChild, data);
   else if (data > node->data)
      node->rightChild = insertNode(node->rightChild, data);
   else
      return node;
   node->height = 1 + max(height(node->leftChild),
                     height(node->rightChild));
   int balance = getBalance(node);
   if (balance > 1 && data < node->leftChild->data)
      return rightRotate(node);
   if (balance < -1 && data > node->rightChild->data)
      return leftRotate(node);
   if (balance > 1 && data > node->leftChild->data) {
      node->leftChild = leftRotate(node->leftChild);
      return rightRotate(node);
   }
   if (balance < -1 && data < node->rightChild->data) {
      node->rightChild = rightRotate(node->rightChild);
      return leftRotate(node);
   }
   return node;
}
struct Node *minValueNode(struct Node *node){
   struct Node *current = node;
   while (current->leftChild != NULL)
      current = current->leftChild;
   return current;
}
struct Node *deleteNode(struct Node *root, int data){
   if (root == NULL)
      return root;
   if (data < root->data)
      root->leftChild = deleteNode(root->leftChild, data);
   else if (data > root->data)
      root->rightChild = deleteNode(root->rightChild, data);
   else {
      if ((root->leftChild == NULL) || (root->rightChild == NULL)) {
         struct Node *temp = root->leftChild ? root->leftChild : root->rightChild;
         if (temp == NULL) {
            temp = root;
            root = NULL;
         } else
            *root = *temp;
         free(temp);
      } else {
         struct Node *temp = minValueNode(root->rightChild);
         root->data = temp->data;
         root->rightChild = deleteNode(root->rightChild, temp->data);
      }
   }
   if (root == NULL)
      return root;
   root->height = 1 + max(height(root->leftChild),
                     height(root->rightChild));
   int balance = getBalance(root);
   if (balance > 1 && getBalance(root->leftChild) >= 0)
      return rightRotate(root);
   if (balance > 1 && getBalance(root->leftChild) < 0) {
      root->leftChild = leftRotate(root->leftChild);
      return rightRotate(root);
   }
   if (balance < -1 && getBalance(root->rightChild) <= 0)
      return leftRotate(root);
   if (balance < -1 && getBalance(root->rightChild) > 0) {
      root->rightChild = rightRotate(root->rightChild);
      return leftRotate(root);
   }
   return root;
}

// Print the tree
void printTree(struct Node *root){
   if (root != NULL) {
      printTree(root->leftChild);
      printf("%d ", root->data);
      printTree(root->rightChild);
   }
}
int main(){
   struct Node *root = NULL;
   root = insertNode(root, 22);
   root = insertNode(root, 14);
   root = insertNode(root, 72);
   root = insertNode(root, 44);
   root = insertNode(root, 25);
   root = insertNode(root, 63);
   root = insertNode(root, 98);
   printf("AVL Tree: ");
   printTree(root);
   root = deleteNode(root, 25);
   printf("\nAfter deletion: ");
   printTree(root);
   return 0;
}

Output

AVL Tree: 14 22 25 44 63 72 98 
After deletion: 14 22 44 63 72 98

import java.util.*;
import java.io.*;
class Node {
   int key, height;
   Node left, right;
   Node (int d) {
      key = d;
      height = 1;
   }
}
public class AVLTree {
   Node root;
   int height (Node N) {
      if (N == null)
         return 0;
      return N.height;
   }
   int max (int a, int b) {
      return (a > b) ? a : b;
   }
   Node rightRotate (Node y) {
      Node x = y.left;
      Node T2 = x.right;
      x.right = y;
      y.left = T2;
      y.height = max (height (y.left), height (y.right)) + 1;
      x.height = max (height (x.left), height (x.right)) + 1;
      return x;
   }
   Node leftRotate (Node x) {
      Node y = x.right;
      Node T2 = y.left;
      y.left = x;
      x.right = T2;
      x.height = max (height (x.left), height (x.right)) + 1;
      y.height = max (height (y.left), height (y.right)) + 1;
      return y;
   }
   int getBalance (Node N) {
      if (N == null)
         return 0;
      return height (N.left) - height (N.right);
   }
   Node insert (Node node, int key) {
      if (node == null)
         return (new Node (key));
      if (key < node.key)
         node.left = insert (node.left, key);
      else if (key > node.key)
         node.right = insert (node.right, key);
      else
         return node;
      node.height = 1 + max (height (node.left), height (node.right));
      int balance = getBalance (node);
      if (balance > 1 && key < node.left.key)
         return rightRotate (node);
      if (balance < -1 && key > node.right.key)
         return leftRotate (node);
      if (balance > 1 && key > node.left.key) {
         node.left = leftRotate (node.left);
         return rightRotate (node);
      }
      if (balance < -1 && key < node.right.key) {
         node.right = rightRotate (node.right);
         return leftRotate (node);
      }
      return node;
   }
   Node minValueNode (Node node) {
      Node current = node;
      while (current.left != null)
         current = current.left;
      return current;
   }
   Node deleteNode (Node root, int key) {
      if (root == null)
         return root;
      if (key < root.key)
         root.left = deleteNode (root.left, key);
      else if (key > root.key)
         root.right = deleteNode (root.right, key);
      else {
         if ((root.left == null) || (root.right == null)) {
            Node temp = null;
            if (temp == root.left)
               temp = root.right;
            else
               temp = root.left;
            if (temp == null) {
               temp = root;
               root = null;
            } else
               root = temp;
         } else {
            Node temp = minValueNode (root.right);
            root.key = temp.key;
            root.right = deleteNode (root.right, temp.key);
         }
      }
      if (root == null)
         return root;
      root.height = max (height (root.left), height (root.right)) + 1;
      int balance = getBalance (root);
      if (balance > 1 && getBalance (root.left) >= 0)
         return rightRotate (root);
      if (balance > 1 && getBalance (root.left) < 0) {
         root.left = leftRotate (root.left);
         return rightRotate (root);
      }
      if (balance < -1 && getBalance (root.right) <= 0)
         return leftRotate (root);
      if (balance < -1 && getBalance (root.right) > 0) {
         root.right = rightRotate (root.right);
         return leftRotate (root);
      }
      return root;
   }
   public void printTree(Node root) {
      if (root == null) return;
      printTree(root.left);
      System.out.println(root.key);
      printTree(root.right);
   }
   public static void main (String[]args) {
      AVLTree tree = new AVLTree();
      tree.root = tree.insert (tree.root, 10);
      tree.root = tree.insert (tree.root, 11);
      tree.root = tree.insert (tree.root, 12);
      tree.root = tree.insert (tree.root, 13);
      tree.root = tree.insert (tree.root, 14);
      tree.root = tree.insert (tree.root, 15);
      System.out.println("The AVL Tree is: ");
      tree.printTree(tree.root);
      tree.root = tree.deleteNode (tree.root, 10);
      System.out.println("\n----------------------------------------------\n");
      System.out.println("The AVL Tree after deleting 10 is: ");
      tree.printTree(tree.root);
      System.out.println ("");
   }
}

Output

The AVL Tree is:
10
11
12
13
14
15
----------------------------------------------
The AVL Tree after deleting 10 is:
11
12
13
14
15

class Node(object):
   def __init__(self, data):
      self.data = data
      self.left = None
      self.right = None
      self.height = 1
class AVLTree(object):
   def insert(self, root, key):
      if not root:
         return Node(key)
      elif key < root.data:
         root.left = self.insert(root.left, key)
      else:
         root.right = self.insert(root.right, key)
      root.h = 1 + max(self.getHeight(root.left),
         self.getHeight(root.right))
      b = self.getBalance(root)
      if b > 1 and key < root.left.data:
         return self.rightRotate(root)
      if b < -1 and key > root.right.data:
         return self.leftRotate(root)
      if b > 1 and key > root.left.data:
         root.left = self.lefttRotate(root.left)
         return self.rightRotate(root)
      if b < -1 and key < root.right.data:
         root.right = self.rightRotate(root.right)
         return self.leftRotate(root)
      return root
   def delete(self, root, key):
      if not root:
         return root
      elif key < root.data:
         root.left = self.delete(root.left, key)
      elif key > root.data:
         root.right = self.delete(root.right, key)
      else:
         if root.left is None:
            temp = root.right
            root = None
            return temp
         elif root.right is None:
            temp = root.left
            root = None
            return temp
         temp = self.getMindataueNode(root.right)
         root.data = temp.data
         root.right = self.delete(root.right, temp.data)

      if root is None:
         return root
      root.height = 1 + max(self.getHeight(root.left), self.getHeight(root.right))
      balance = self.getBalance(root)
      if balance > 1 and self.getBalance(root.left) >= 0:
         return self.rightRotate(root)
      if balance < -1 and self.getBalance(root.right) <= 0:
         return self.leftRotate(root)
      if balance > 1 and self.getBalance(root.left) < 0:
         root.left = self.leftRotate(root.left)
         return self.rightRotate(root)
      if balance < -1 and self.getBalance(root.right) > 0:
         root.right = self.rightRotate(root.right)
         return self.leftRotate(root)
      return root
   def leftRotate(self, z):
      y = z.right
      T2 = y.left
      y.left = z
      z.right = T2
      z.height = 1 + max(self.getHeight(z.left),
         self.getHeight(z.right))
      y.height = 1 + max(self.getHeight(y.left),
         self.getHeight(y.right))
      return y
   def rightRotate(self, z):
      y = z.left
      T3 = y.right
      y.right = z
      z.left = T3
      z.height = 1 + max(self.getHeight(z.left),
         self.getHeight(z.right))
      y.height = 1 + max(self.getHeight(y.left),
         self.getHeight(y.right))
      return y
   def getHeight(self, root):
      if not root:
         return 0
      return root.height
   def getBalance(self, root):
      if not root:
         return 0
      return self.getHeight(root.left) - self.getHeight(root.right)
   def Inorder(self, root):
      if root.left:
         self.Inorder(root.left)
      print(root.data)
      if root.right:
         self.Inorder(root.right)
Tree = AVLTree()
root = None
root = Tree.insert(root, 10)
root = Tree.insert(root, 13)
root = Tree.insert(root, 11)
root = Tree.insert(root, 14)
root = Tree.insert(root, 12)
root = Tree.insert(root, 15)

# Inorder Traversal
print("Inorder traversal of the AVL tree is")
Tree.Inorder(root)
root = Tree.delete(root, 14)
print("Inorder traversal of the modified AVL tree is")
Tree.Inorder(root)

Output

Inorder traversal of the AVL tree is
10
11
12
13
14
15
Inorder traversal of the modified AVL tree is
10
11
12
13
15

Data Structure and Algorithms - Red Black Trees

Red-Black Trees are another type of the Balanced Binary Search Trees with two coloured nodes: Red and Black. It is a self-balancing binary search tree that makes use of these colours to maintain the balance factor during the insertion and deletion operations. Hence, during the Red-Black Tree operations, the memory uses 1 bit of storage to accommodate the colour information of each node

In Red-Black trees, also known as RB trees, there are different conditions to follow while assigning the colours to the nodes.

The root node is always black in colour.
No two adjacent nodes must be red in colour.
Every path in the tree (from the root node to the leaf node) must have the same amount of black coloured nodes.

Even though AVL trees are more balanced than RB trees, with the balancing algorithm in AVL trees being stricter than that of RB trees, multiple and faster insertion and deletion operations are made more efficient through RB trees.

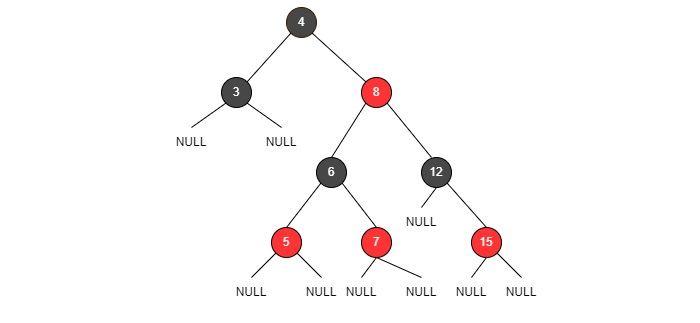
Fig: RB trees

Basic Operations of Red-Black Trees

The operations on Red-Black Trees include all the basic operations usually performed on a Binary Search Tree. Some of the basic operations of an RB Tree include −

Insertion
Deletion
Search

Insertion operation of a Red-Black tree follows the same insertion algorithm of a binary search tree. The elements are inserted following the binary search property and as an addition, the nodes are color coded as red and black to balance the tree according to the red-black tree properties.

Follow the procedure given below to insert an element into a red-black tree by maintaining both binary search tree and red black tree properties.

Case 1 − Check whether the tree is empty; make the current node as the root and color the node black if it is empty.

Case 2 − But if the tree is not empty, we create a new node and color it red. Here we face two different cases −

If the parent of the new node is a black colored node, we exit the operation and tree is left as it is.
If the parent of this new node is red and the color of the parent’s sibling is either black or if it does not exist, we apply a suitable rotation and recolor accordingly.
If the parent of this new node is red and color of the parent’s sibling is red, recolor the parent, the sibling and grandparent nodes to black. The grandparent is recolored only if it is not the root node; if it is the root node recolor only the parent and the sibling.

Insertion Example

Let us construct an RB Tree for the first 7 integer numbers to understand the insertion operation in detail −

The tree is checked to be empty so the first node added is a root and is colored black.

Now, the tree is not empty so we create a new node and add the next integer with color red,

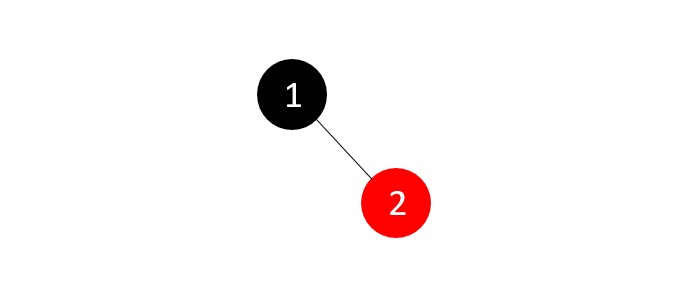
The nodes do not violate the binary search tree and RB tree properties, hence we move ahead to add another node.

The tree is not empty; we create a new red node with the next integer to it. But the parent of the new node is not a black colored node,

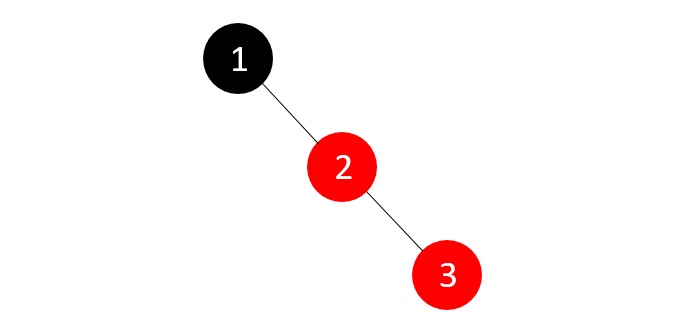
The tree right now violates both the binary search tree and RB tree properties; since parent’s sibling is NULL, we apply a suitable rotation and recolor the nodes.

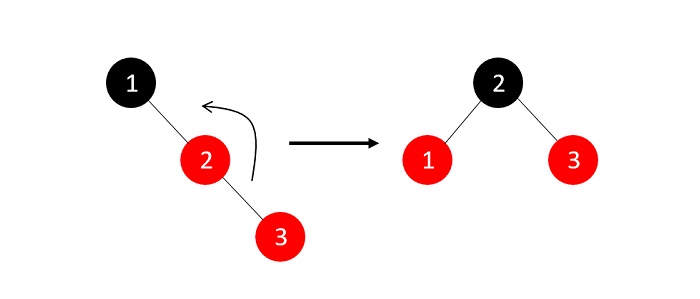
Now that the RB Tree property is restored, we add another node to the tree −

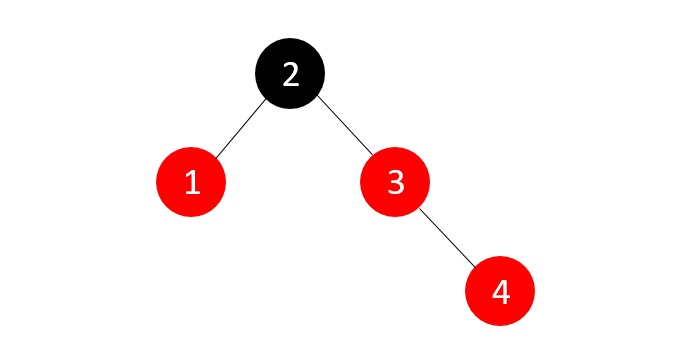
The tree once again violates the RB Tree balance property, so we check for the parent’s sibling node color, red in this case, so we just recolor the parent and the sibling.

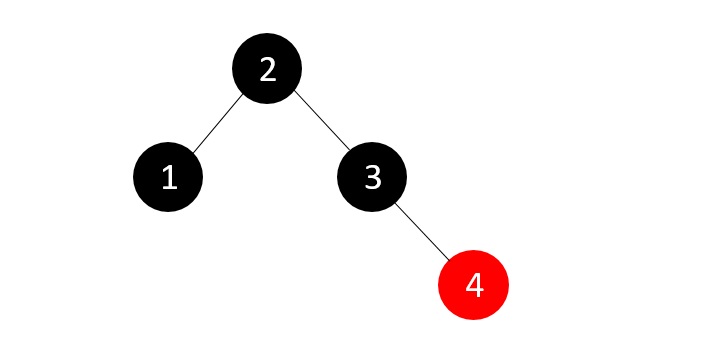
We next insert the element 5, which makes the tree violate the RB Tree balance property once again.

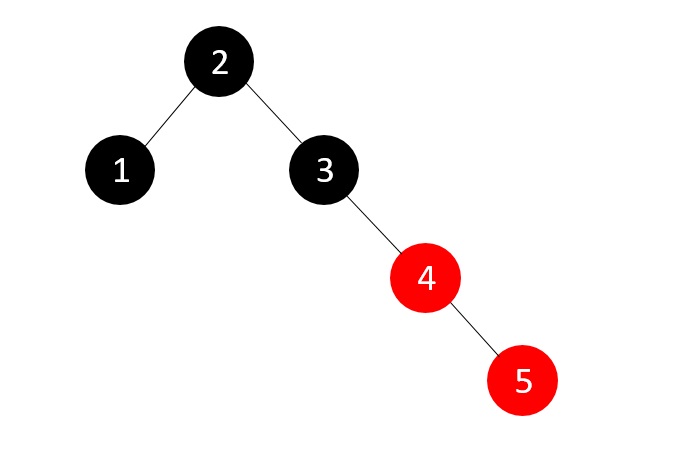
And since the sibling is NULL, we apply suitable rotation and recolor.

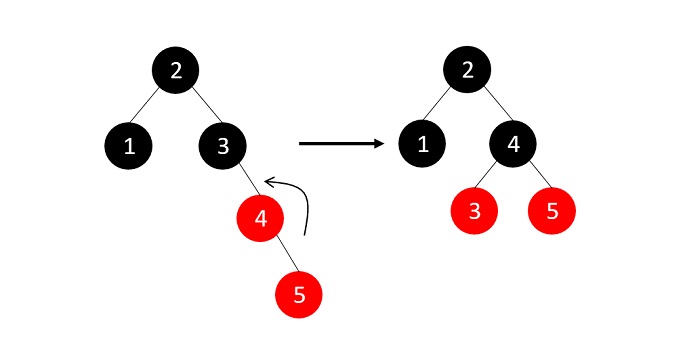
Now, we insert element 6, but the RB Tree property is violated and one of the insertion cases need to be applied −

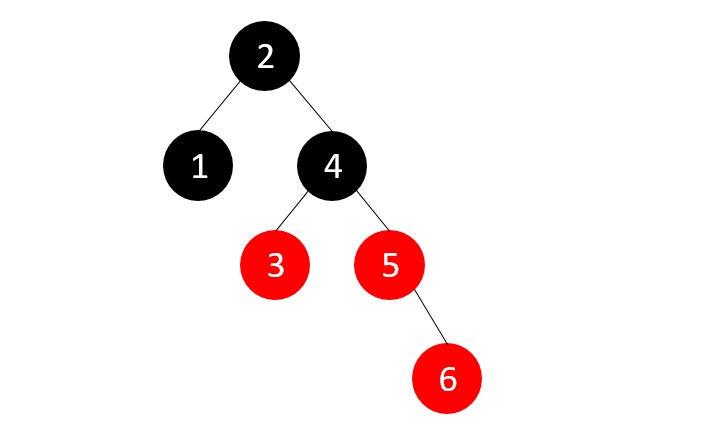
The parent’s sibling is red, so we recolor the parent, parent’s sibling and the grandparent nodes since the grandparent is not the root node.

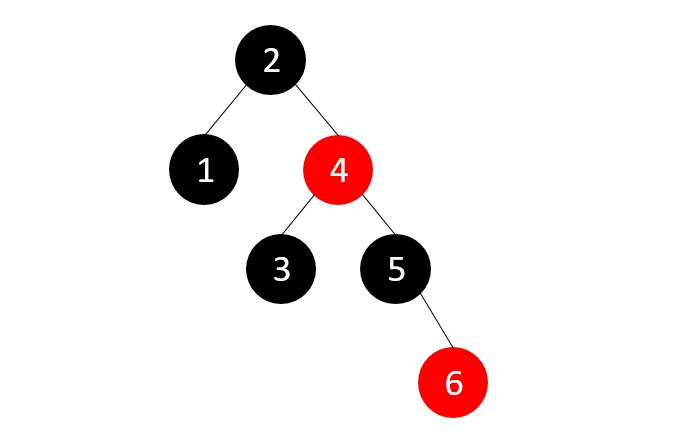
Now, we add the last element, 7, but the parent node of this new node is red.

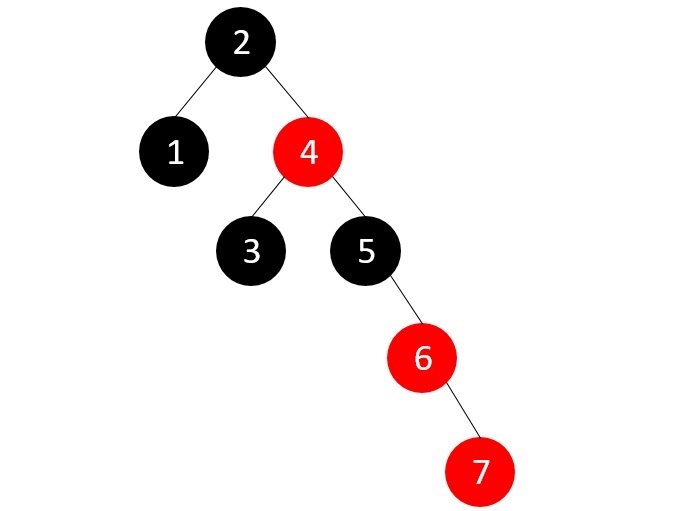
Since the parent’s sibling is NULL, we apply suitable rotations (RR rotation)

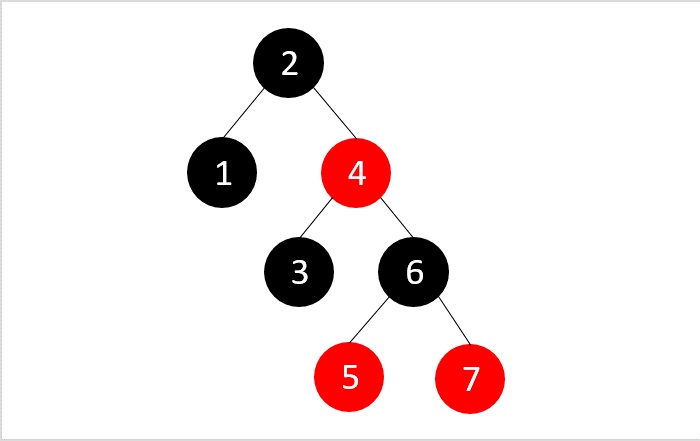
The final RB Tree is achieved.

Deletion

The deletion operation on red black tree must be performed in such a way that it must restore all the properties of a binary search tree and a red black tree. Follow the steps below to perform the deletion operation on the red black tree −

Firstly, we perform deletion based on the binary search tree properties.

Case 1 − If either the node to be deleted or the node’s parent is red, just delete it.

Case 2 − If the node is a double black, just remove the double black (double black occurs when the node to be deleted is a black colored leaf node, as it adds up the NULL nodes which are considered black colored nodes too)

Case 3 − If the double black’s sibling node is also a black node and its child nodes are also black in color, follow the steps below −

Remove double black
Recolor its parent to black (if the parent is a red node, it becomes black; if the parent is already a black node, it becomes double black)
Recolor the parent’s sibling with red
If double black node still exists, we apply other cases.

Case 4 − If the double black node’s sibling is red, we perform the following steps −

Swap the colors of the parent node and the parent’s sibling node.
Rotate parent node in the double black’s direction
Reapply other cases that are suitable.

Case 5 − If the double black’s sibling is a black node but the sibling’s child node that is closest to the double black is red, follows the steps below −

Swap the colors of double black’s sibling and the sibling’s child in question
Rotate the sibling node is the opposite direction of double black (i.e. if the double black is a right child apply left rotations and vice versa)
Apply case 6.

Case 6 − If the double black’s sibling is a black node but the sibling’s child node that is farther to the double black is red, follows the steps below −

Swap the colors of double black’s parent and sibling nodes
Rotate the parent in double black’s direction (i.e. if the double black is a right child apply right rotations and vice versa)
Remove double black
Change the color of red child node to black.

Deletion Example

Considering the same constructed Red-Black Tree above, let us delete few elements from the tree.

Delete elements 4, 5, 3 from the tree.

To delete the element 4, let us perform the binary search deletion first.

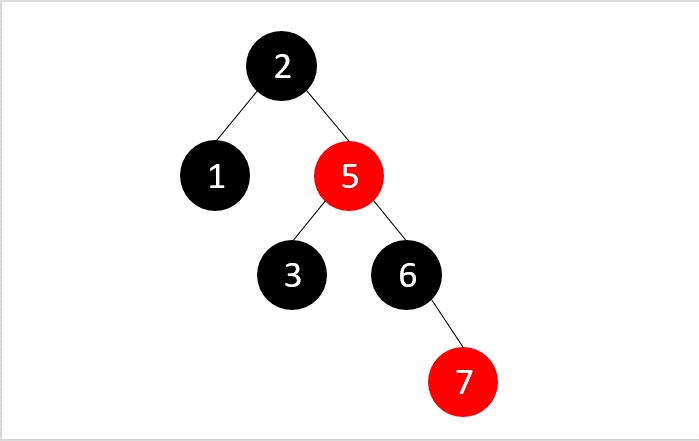
After performing the binary search deletion, the RB Tree property is not disturbed, therefore the tree is left as it is.

Then, we delete the element 5 using the binary search deletion

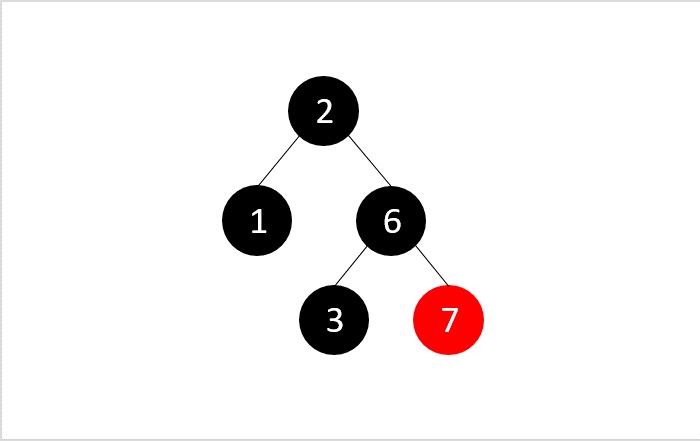
But the RB property is violated after performing the binary search deletion, i.e., all the paths in the tree do not hold same number of black nodes; so we swap the colors to balance the tree.

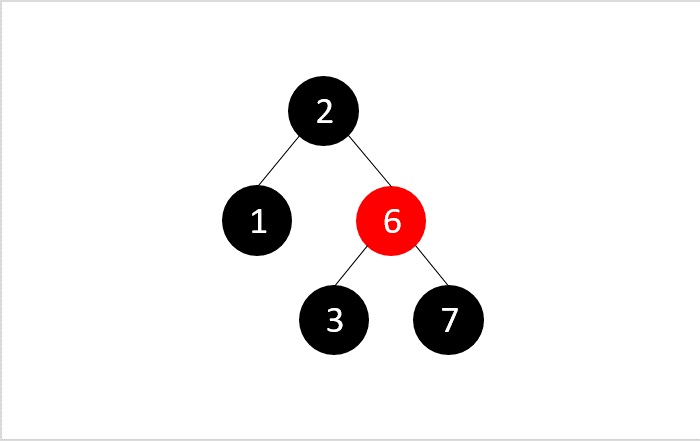
Then, we delete the node 3 from the tree obtained −

Applying binary search deletion, we delete node 3 normally as it is a leaf node. And we get a double node as 3 is a black colored node.

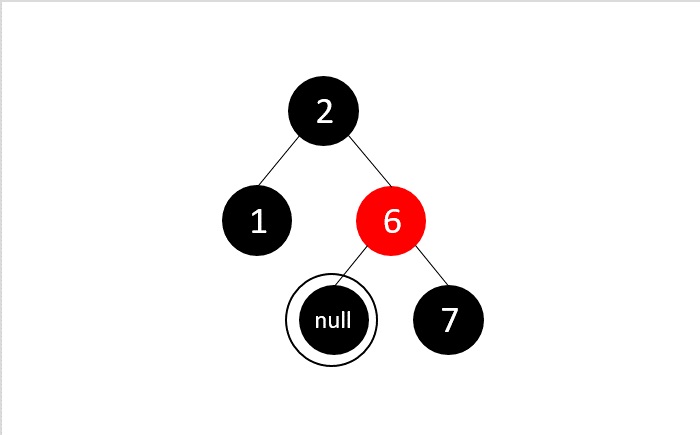
We apply case 3 deletion as double black’s sibling node is black and its child nodes are also black. Here, we remove the double black, recolor the double black’s parent and sibling.

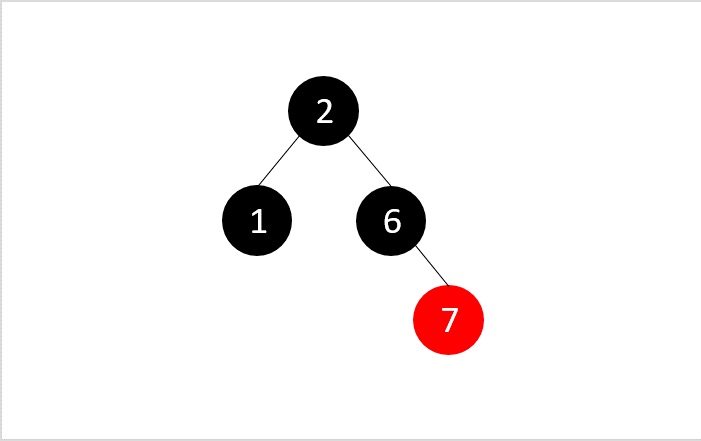
All the desired nodes are deleted and the RB Tree property is maintained.

Search

The search operation in red-black tree follows the same algorithm as that of a binary search tree. The tree is traversed and each node is compared with the key element to be searched; if found it returns a successful search. Otherwise, it returns an unsuccessful search.

Data Structure and Algorithms - B Trees

B trees are extended binary search trees that are specialized in m-way searching, since the order of B trees is ‘m’. Order of a tree is defined as the maximum number of children a node can accommodate. Therefore, the height of a b tree is relatively smaller than the height of AVL tree and RB tree.

They are general form of a Binary Search Tree as it holds more than one key and two children.

The various properties of B trees include −

Every node in a B Tree will hold a maximum of m children and (m-1) keys, since the order of the tree is m.
Every node in a B tree, except root and leaf, can hold at least m/2 children
The root node must have no less than two children.
All the paths in a B tree must end at the same level, i.e. the leaf nodes must be at the same level.
A B tree always maintains sorted data.

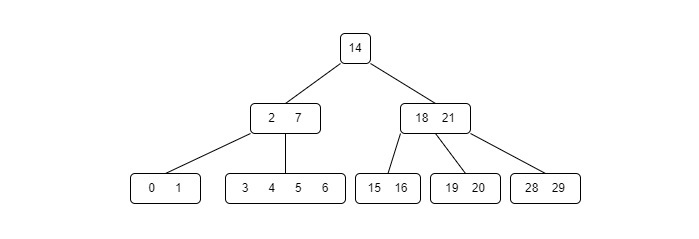
B trees are also widely used in disk access, minimizing the disk access time since the height of a b tree is low.

Note − A disk access is the memory access to the computer disk where the information is stored and disk access time is the time taken by the system to access the disk memory.

Basic Operations of B Trees

The operations supported in B trees are Insertion, deletion and searching with the time complexity of O(log n) for every operation.

Insertion

The insertion operation for a B Tree is done similar to the Binary Search Tree but the elements are inserted into the same node until the maximum keys are reached. The insertion is done using the following procedure −

Step 1 − Calculate the maximum $\mathrm{\left ( m-1 \right )}$ and minimum $\mathrm{\left ( \left \lceil \frac{m}{2}\right \rceil-1 \right )}$ number of keys a node can hold, where m is denoted by the order of the B Tree.

Step 2 − The data is inserted into the tree using the binary search insertion and once the keys reach the maximum number, the node is split into half and the median key becomes the internal node while the left and right keys become its children.

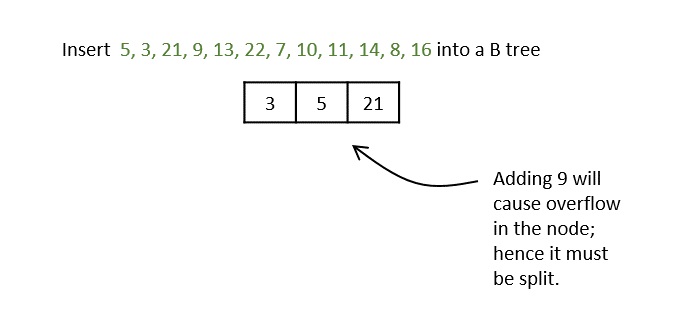
Step 3 − All the leaf nodes must be on the same level.

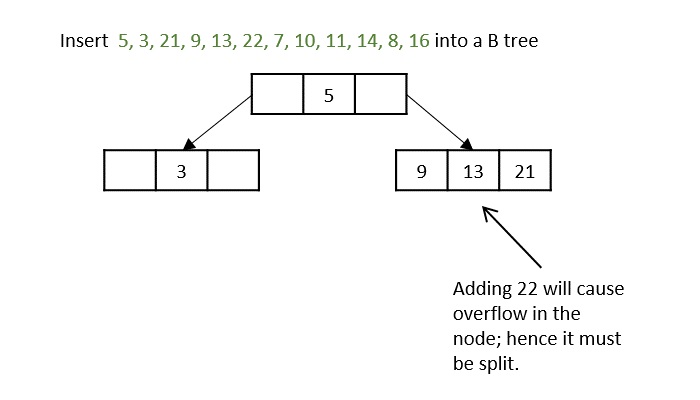
The keys, 5, 3, 21, 9, 13 are all added into the node according to the binary search property but if we add the key 22, it will violate the maximum key property. Hence, the node is split in half, the median key is shifted to the parent node and the insertion is then continued.

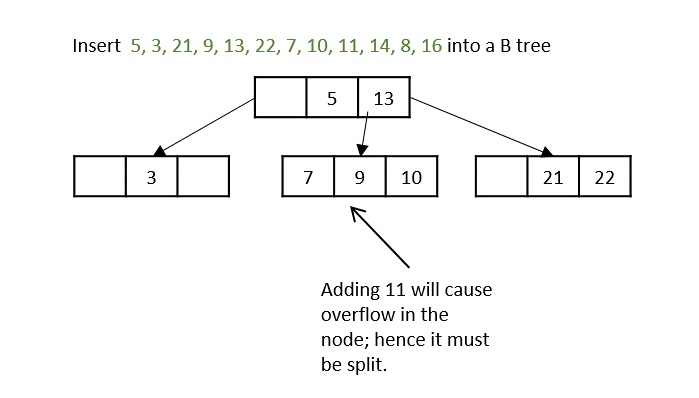
Another hiccup occurs during the insertion of 11, so the node is split and median is shifted to the parent.

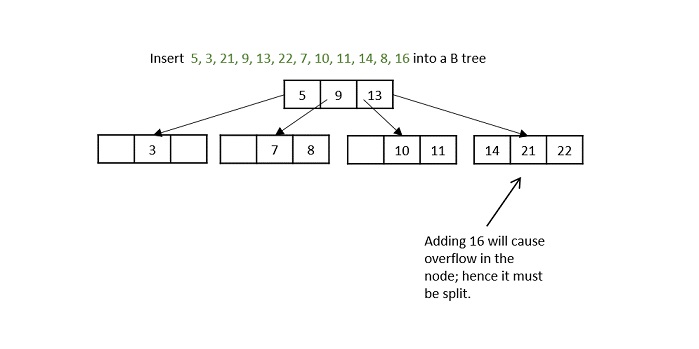
While inserting 16, even if the node is split in two parts, the parent node also overflows as it reached the maximum keys. Hence, the parent node is split first and the median key becomes the root. Then, the leaf node is split in half the median of leaf node is shifted to its parent.

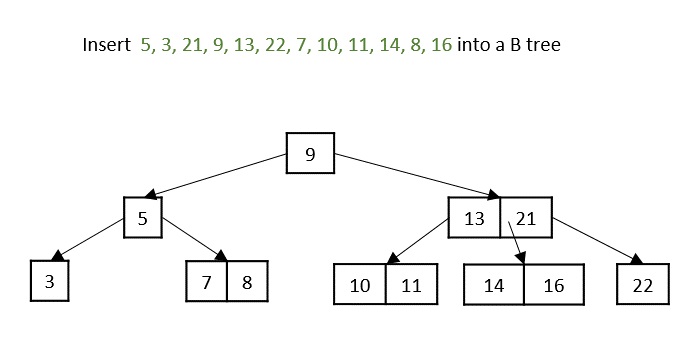
The final B tree after inserting all the elements is achieved.

Example

// Insert the value
void insertion(int item) {
   int flag, i;
   struct btreeNode *child;
   flag = setNodeValue(item, &i, root, &child);
   if (flag)
      root = createNode(i, child);
}

Deletion

The deletion operation in a B tree is slightly different from the deletion operation of a Binary Search Tree. The procedure to delete a node from a B tree is as follows −

Case 1 − If the key to be deleted is in a leaf node and the deletion does not violate the minimum key property, just delete the node.

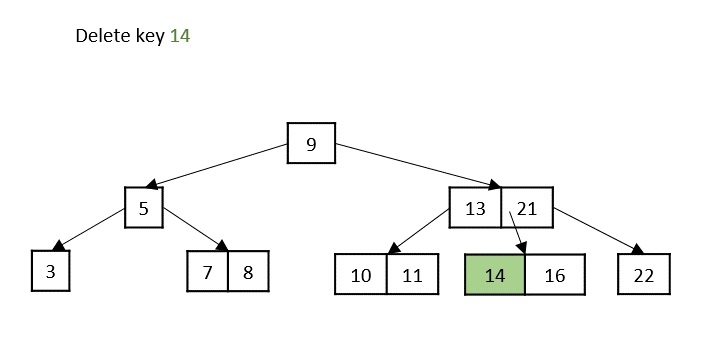
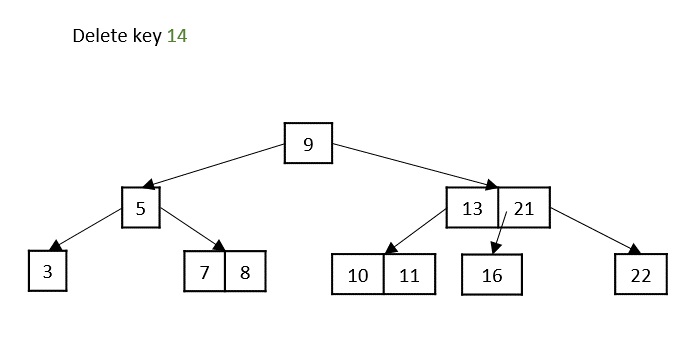
Case 2 − If the key to be deleted is in a leaf node but the deletion violates the minimum key property, borrow a key from either its left sibling or right sibling. In case if both siblings have exact minimum number of keys, merge the node in either of them.

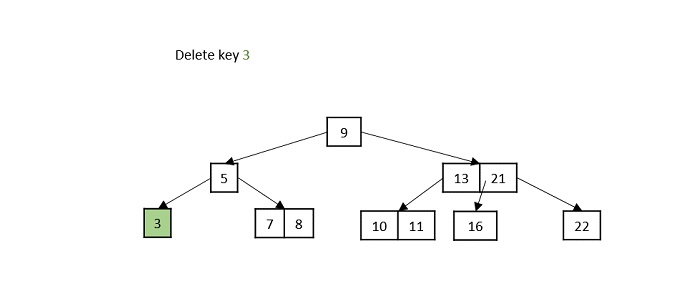
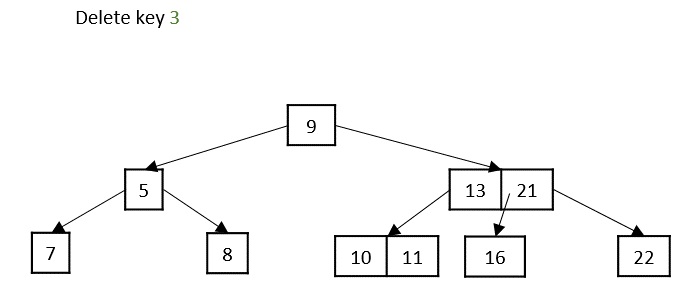
Case 3 − If the key to be deleted is in an internal node, it is replaced by a key in either left child or right child based on which child has more keys. But if both child nodes have minimum number of keys, they’re merged together.

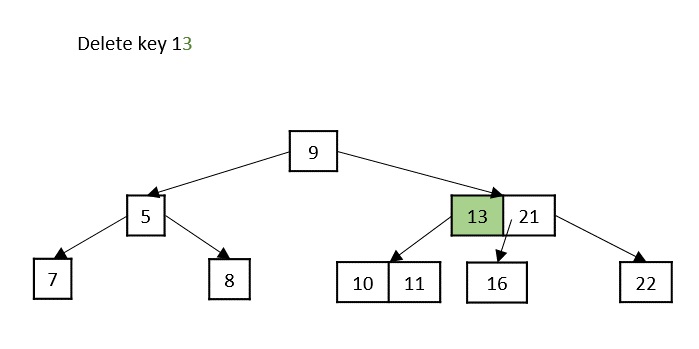
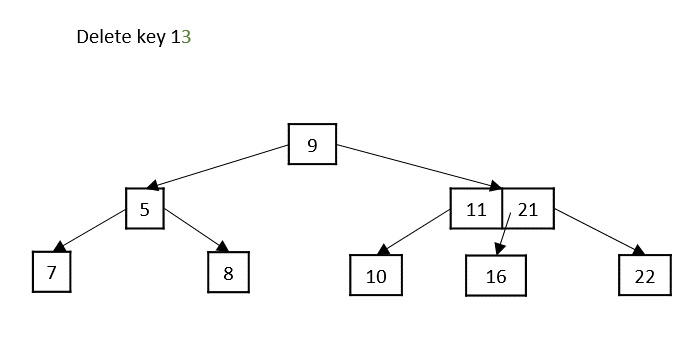
Case 4 − If the key to be deleted is in an internal node violating the minimum keys property, and both its children and sibling have minimum number of keys, merge the children. Then merge its sibling with its parent.

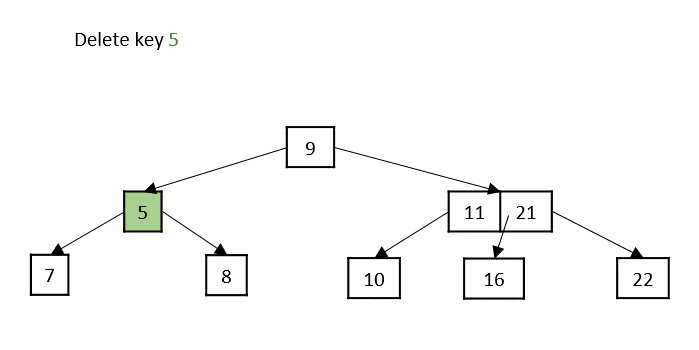
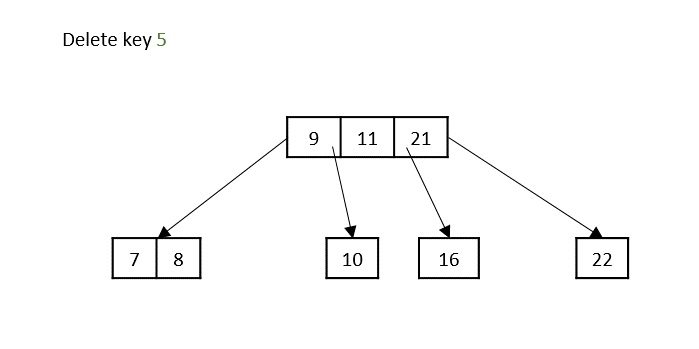
Following is functional C++ code snippet of the deletion operation in B Trees −

// Deletion operation
void deletion(int key){
   int index = searchkey(key);
   if (index < n && keys[index] == key) {
      if (leaf)
         deletion_at_leaf(index);
      else
         deletion_at_nonleaf(index);
   } else {
      if (leaf) {
         cout << "key " << key << " does not exist in the tree\n";
         return;
      }
      bool flag = ((index == n) ? true : false);
      if (C[index]->n < t)
         fill(index);
      if (flag && index > n)
         C[index - 1]->deletion(key);
      else
         C[index]->deletion(key);
   }
   return;
}

// Deletion at the leaf nodes
void deletion_at_leaf(int index){
   for (int i = index + 1; i < n; ++i)
      keys[i - 1] = keys[i];
   n--;
   return;
}

// Deletion at the non leaf node
void deletion_at_nonleaf(int index){
   int key = keys[index];
   if (C[index]->n >= t) {
      int pred = get_Predecessor(index);
      keys[index] = pred;
      C[index]->deletion(pred);
   } else if (C[index + 1]->n >= t) {
      int successor = copysuccessoressor(index);
      keys[index] = successor;
      C[index + 1]->deletion(successor);
   } else {
      merge(index);
      C[index]->deletion(key);
   }
   return;
}

C++ Implementation

Following is the complete implementation of B Trees in C++ −

#include<iostream>
using namespace std;
struct BTree {//node declaration
   int *d;
   BTree **child_ptr;
   bool l;
   int n;
}*r = NULL, *np = NULL, *x = NULL;

BTree* init() {//creation of node
   int i;
   np = new BTree;
   np->d = new int[6];//order 6
   np->child_ptr = new BTree *[7];
   np->l = true;
   np->n = 0;
   for (i = 0; i < 7; i++) {
      np->child_ptr[i] = NULL;
   }
   return np;
}

void traverse(BTree *p) { //traverse the tree
   cout<<endl;
   int i;
   for (i = 0; i < p->n; i++) {
      if (p->l == false) {
         traverse(p->child_ptr[i]);
      }
      cout << " " << p->d[i];
   }
   if (p->l == false) {
      traverse(p->child_ptr[i]);
   }
   cout<<endl;
}

void sort(int *p, int n){ //sort the tree
   int i, j, t;
   for (i = 0; i < n; i++) {
      for (j = i; j <= n; j++) {
         if (p[i] >p[j]) {
            t = p[i];
            p[i] = p[j];
            p[j] = t;
         }
      }
   }
}

int split_child(BTree *x, int i) {
   int j, mid;
   BTree *np1, *np3, *y;
   np3 = init();//create new node
   np3->l = true;
   if (i == -1) {
      mid = x->d[2];//find mid
      x->d[2] = 0;
      x->n--;
      np1 = init();
      np1->l= false;
      x->l= true;
      for (j = 3; j < 6; j++) {
         np3->d[j - 3] = x->d[j];
         np3->child_ptr[j - 3] = x->child_ptr[j];
         np3->n++;
         x->d[j] = 0;
         x->n--;
      }
      for (j = 0; j < 6; j++) {
         x->child_ptr[j] = NULL;
      }
      np1->d[0] = mid;
      np1->child_ptr[np1->n] = x;
      np1->child_ptr[np1->n + 1] = np3;
      np1->n++;
      r = np1;
   } else {
      y = x->child_ptr[i];
      mid = y->d[2];
      y->d[2] = 0;
      y->n--;
      for (j = 3; j <6 ; j++) {
         np3->d[j - 3] = y->d[j];
         np3->n++;
         y->d[j] = 0;
         y->n--;
      }
      x->child_ptr[i + 1] = y;
      x->child_ptr[i + 1] = np3;
   }
   return mid;
}

void insert(int a) {
   int i, t;
   x = r;
   if (x == NULL) {
      r = init();
      x = r;
   } else {
      if (x->l== true && x->n == 6) {
         t = split_child(x, -1);
         x = r;
         for (i = 0; i < (x->n); i++) {
            if ((a >x->d[i]) && (a < x->d[i + 1])) {
               i++;
               break;
            } else if (a < x->d[0]) {
               break;
            } else {
               continue;
            }
         }
         x = x->child_ptr[i];
      } else {
         while (x->l == false) {
            for (i = 0; i < (x->n); i++) {
               if ((a >x->d[i]) && (a < x->d[i + 1])) {
                  i++;
                  break;
               } else if (a < x->d[0]) {
                  break;
               } else {
                  continue;
               }
            }
            if ((x->child_ptr[i])->n == 6) {
               t = split_child(x, i);
               x->d[x->n] = t;
               x->n++;
               continue;
            } else {
               x = x->child_ptr[i];
            }
         }
      }
   }
   x->d[x->n] = a;
   sort(x->d, x->n);
   x->n++;
}

int main() {
   int i, n, t;
   insert(10);
   insert(20);
   insert(30);
   insert(40);
   insert(50);
   cout<<"B tree:\n";
   traverse(r);
}

Output

B tree:
10 20 30 40 50

Data Structure and Algorithms - B+ Trees

The B+ trees are extensions of B trees designed to make the insertion, deletion and searching operations more efficient.

The properties of B+ trees are similar to the properties of B trees, except that the B trees can store keys and records in all internal nodes and leaf nodes while B+ trees store records in leaf nodes and keys in internal nodes. One profound property of the B+ tree is that all the leaf nodes are connected to each other in a single linked list format and a data pointer is available to point to the data present in disk file. This helps fetch the records in equal numbers of disk access.

Since the size of main memory is limited, B+ trees act as the data storage for the records that couldn’t be stored in the main memory. For this, the internal nodes are stored in the main memory and the leaf nodes are stored in the secondary memory storage.

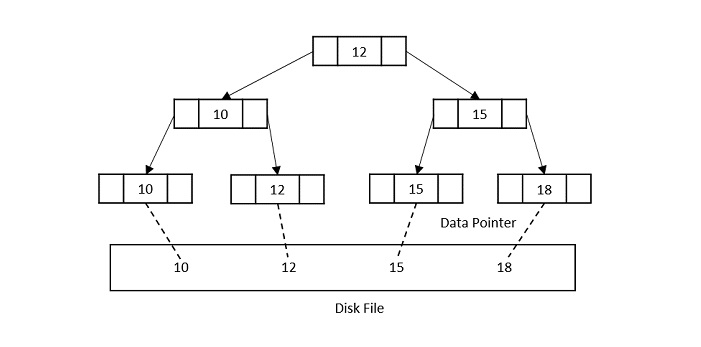
Properties of B+ trees

Every node in a B+ Tree, except root, will hold a maximum of m children and (m-1) keys, and a minimum of $\mathrm{\left \lceil \frac{m}{2}\right \rceil}$ children and $\mathrm{\left \lceil \frac{m-1}{2}\right \rceil}$ keys, since the order of the tree is m.
The root node must have no less than two children and at least one search key.
All the paths in a B tree must end at the same level, i.e. the leaf nodes must be at the same level.
A B+ tree always maintains sorted data.

Basic Operations of B+ Trees

The operations supported in B+ trees are Insertion, deletion and searching with the time complexity of O(log n) for every operation.

They are almost similar to the B tree operations as the base idea to store data in both data structures is same. However, the difference occurs as the data is stored only in the leaf nodes of a B+ trees, unlike B trees.

Insertion

The insertion to a B+ tree starts at a leaf node.

Step 1 − Calculate the maximum and minimum number of keys to be added onto the B+ tree node.

Step 2 − Insert the elements one by one accordingly into a leaf node until it exceeds the maximum key number.

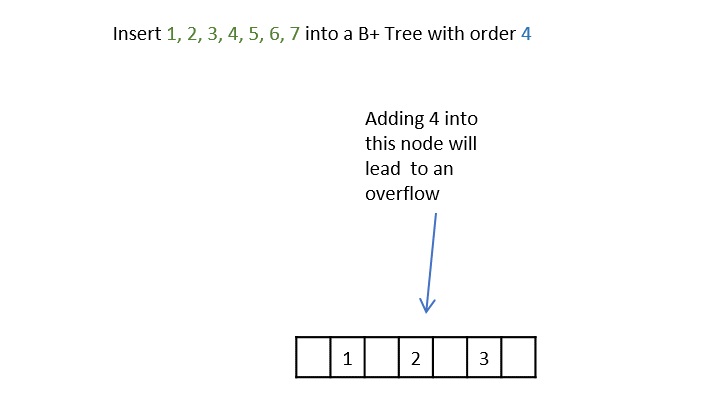
Step 3 − The node is split into half where the left child consists of minimum number of keys and the remaining keys are stored in the right child.

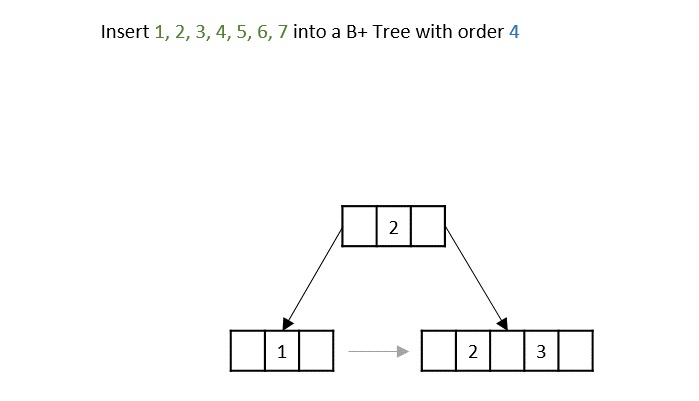
Step 4 − But if the internal node also exceeds the maximum key property, the node is split in half where the left child consists of the minimum keys and remaining keys are stored in the right child. However, the smallest number in the right child is made the parent.

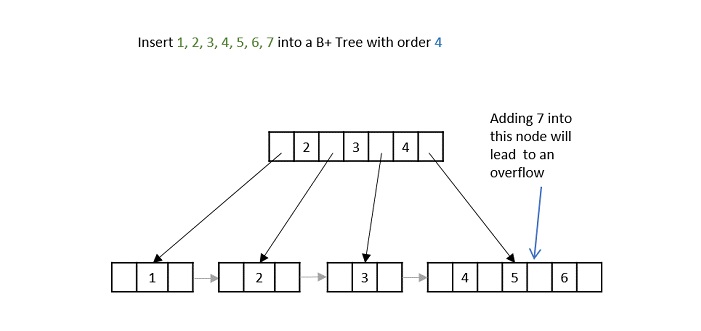
Step 5 − If both the leaf node and internal node have the maximum keys, both of them are split in the similar manner and the smallest key in the right child is added to the parent node.

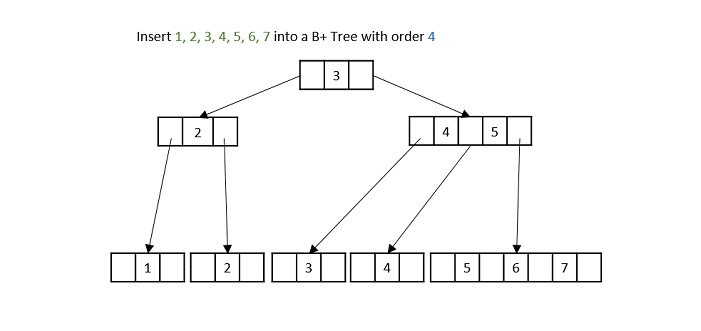
Deletion

The deletion operation in a B+ tree, we need to consider the redundancy in the data structure.

Case 1 − If the key is present in a leaf node which has more than minimal number of keys, without its copy present in the internal nodes, simple delete it.

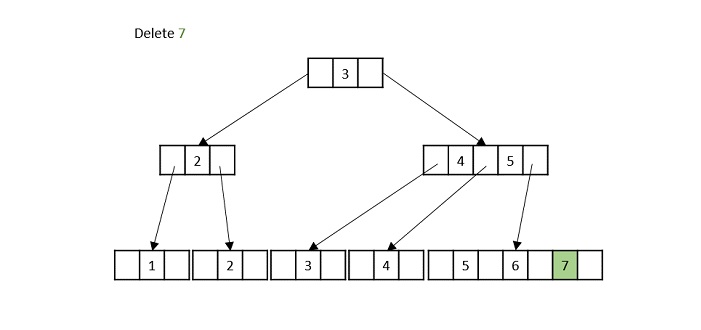
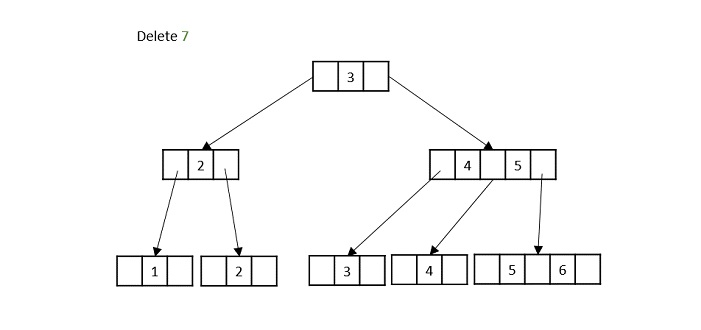
Case 2 − If the key is present in a leaf node with exactly minimal number of keys and a copy of it is not present in the internal nodes, borrow a key from its sibling node and delete the desired key.

Case 3 − If the key present in the leaf node has its copy in the internal nodes, there are multiple scenarios possible −

More than minimal keys present in both leaf node and internal node: simply delete the key and add the inorder successor to the internal node only.

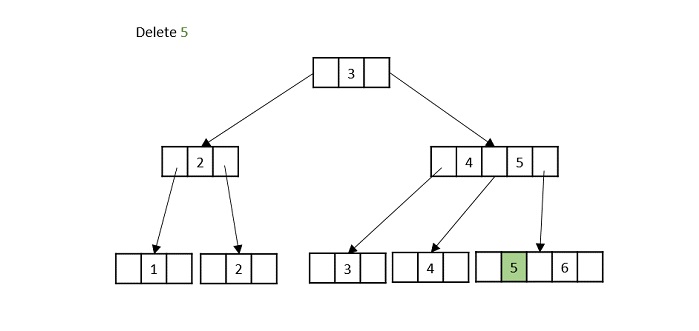
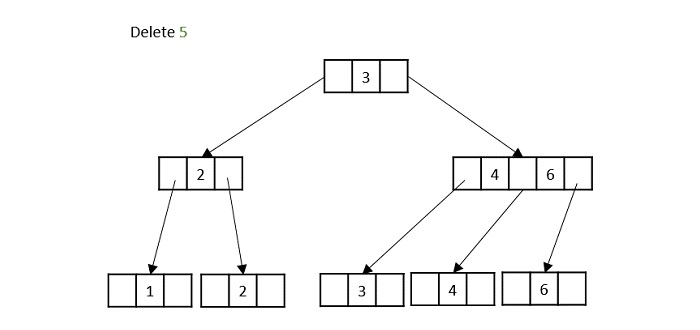
Exact minimum number of keys present in the leaf node: delete the node and borrow a node from its immediate sibling and replace its value in internal node as well.

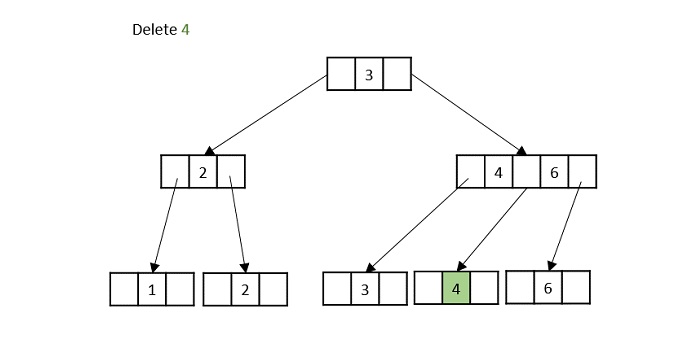
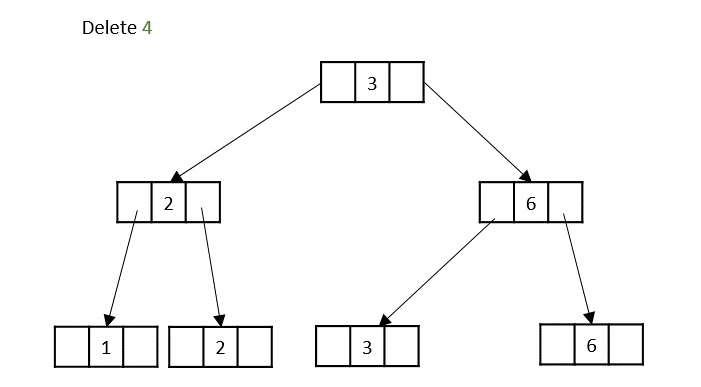
If the copy of the leaf node to be delete is in its grandparent, delete the node and remove the empty space. The grandparent is filled with the inorder successor of the deleted node.

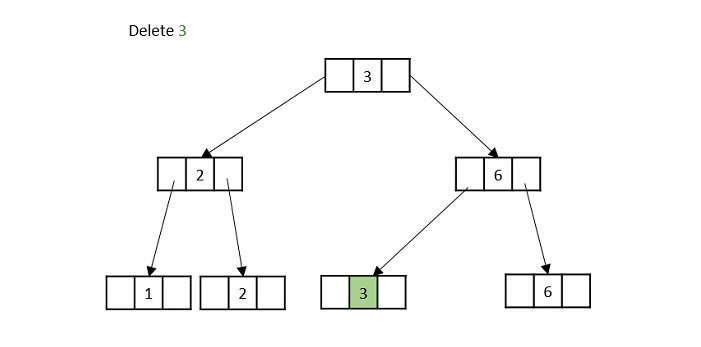
Case 4 − If the key to be deleted is in a node violating the minimum keys property, both its parent and sibling have minimum number of keys, delete the key and merge its sibling with its parent.

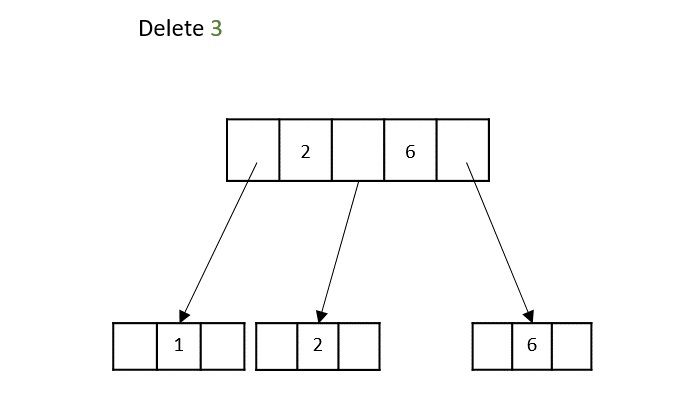
C++ Implementation

Following is the C++ implementation of B+ Trees −

#include<iostream>
using namespace std;
struct BplusTree {
   int *d;
   BplusTree **child_ptr;
   bool l;
   int n;
}
*r = NULL, *np = NULL, *x = NULL;
BplusTree* init() { //to create nodes 
   int i;
   np = new BplusTree;
   np->d = new int[6];//order 6
   np->child_ptr = new BplusTree *[7];
   np->l = true;
   np->n = 0;
   for (i = 0; i < 7; i++) {
      np->child_ptr[i] = NULL;
   }
   return np;
}

void traverse(BplusTree *p) { //traverse tree 
   cout<<endl;
   int i;
   for (i = 0; i < p->n; i++) {
      if (p->l == false) {
         traverse(p->child_ptr[i]);
      }
      cout << " " << p->d[i];
   }
   if (p->l == false) {
      traverse(p->child_ptr[i]);
   }
   cout<<endl;
}

void sort(int *p, int n) { //sort the tree 
   int i, j, t;
   for (i = 0; i < n; i++) {
      for (j = i; j <= n; j++) {
         if (p[i] >p[j]) {
            t = p[i];
            p[i] = p[j];
            p[j] = t;
         }
      }
   }
}

int split_child(BplusTree *x, int i) {
   int j, mid;
   BplusTree *np1, *np3, *y;
   np3 = init();
   np3->l = true;
   if (i == -1) {
      mid = x->d[2];
      x->d[2] = 0;
      x->n--;
      np1 = init();
      np1->l = false;
      x->l = true;
      for (j = 3; j < 6; j++) {
         np3->d[j - 3] = x->d[j];
         np3->child_ptr[j - 3] = x->child_ptr[j];
         np3->n++;
         x->d[j] = 0;
         x->n--;
      }
      for (j = 0; j < 6; j++) {
         x->child_ptr[j] = NULL;
      }
      np1->d[0] = mid;
      np1->child_ptr[np1->n] = x;
      np1->child_ptr[np1->n + 1] = np3;
      np1->n++;
      r = np1;
   } else {
      y = x->child_ptr[i];
      mid = y->d[2];
      y->d[2] = 0;
      y->n--;
      for (j = 3; j <6 ; j++) {
         np3->d[j - 3] = y->d[j];
         np3->n++;
         y->d[j] = 0;
         y->n--;
      }
      x->child_ptr[i + 1] = y;
      x->child_ptr[i + 1] = np3;
   }
   return mid;
}

void insert(int a) {
   int i, t;
   x = r;
   if (x == NULL) {
      r = init();
      x = r;
   } else {
      if (x->l== true && x->n == 6) {
         t = split_child(x, -1);
         x = r;
         for (i = 0; i < (x->n); i++) {
            if ((a >x->d[i]) && (a < x->d[i + 1])) {
            i++;
            break;
         } else if (a < x->d[0]) {
            break;
         } else {
            continue;
         }
      }
      x = x->child_ptr[i];
   } else {
      while (x->l == false) {
         for (i = 0; i < (x->n); i++) {
            if ((a >x->d[i]) && (a < x->d[i + 1])) {
               i++;
               break;
            } else if (a < x->d[0]) {
               break;
            } else {
               continue;
            }
         }
         if ((x->child_ptr[i])->n == 6) {
            t = split_child(x, i);
            x->d[x->n] = t;
            x->n++;
            continue;
         } else {
            x = x->child_ptr[i];
         }
      }
   }
}
   x->d[x->n] = a;
   sort(x->d, x->n);
   x->n++;
}

int main() {
   int i, n, t;
   insert(10);
   insert(20);
   insert(30);
   insert(40);
   insert(50);
   cout<<"B+ tree:\n";
   traverse(r);
}

Output

B+ tree:
10 20 30 40 50

Data Structure and Algorithms - Splay Trees

Splay trees are the altered versions of the Binary Search Trees, since it contains all the operations of BSTs, like insertion, deletion and searching, followed by another extended operation called splaying.

For instance, a value “A” is supposed to be inserted into the tree. If the tree is empty, add “A” to the root of the tree and exit; but if the tree is not empty, use binary search insertion operation to insert the element and then perform splaying on the new node.

Similarly, after searching an element in the splay tree, the node consisting of the element must be splayed as well.

But how do we perform splaying? Splaying, in simpler terms, is just a process to bring an operational node to the root. There are six types of rotations for it.

Zig rotation
Zag rotation
Zig-Zig rotation
Zag-Zag rotation
Zig-Zag rotation
Zag-Zig rotation

Zig rotation

The zig rotations are performed when the operational node is either the root node or the left child node of the root node. The node is rotated towards its right.

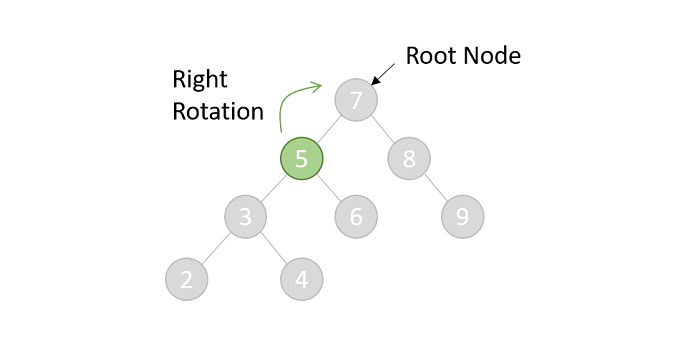
After the shift, the tree will look like −

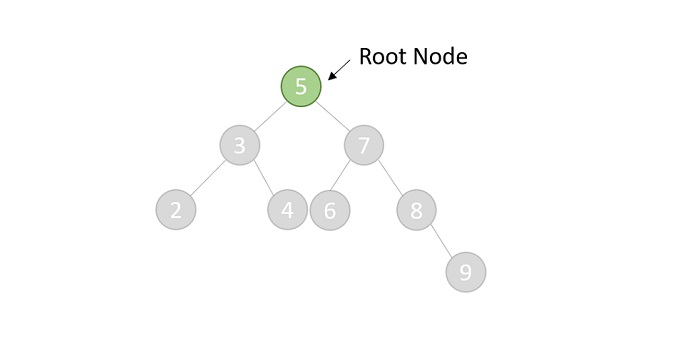
Zag rotation

The zag rotations are also performed when the operational node is either the root node or the right child nod of the root node. The node is rotated towards its left.

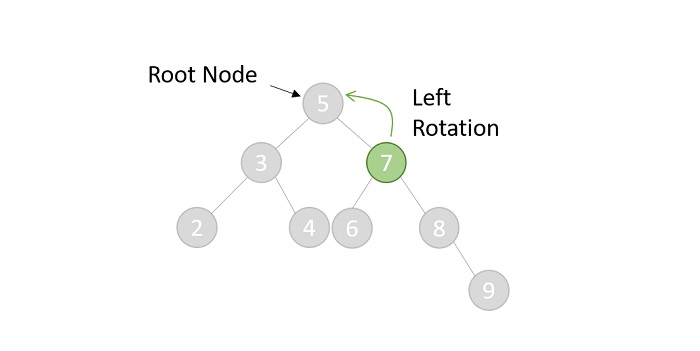
The operational node becomes the root node after the shift −

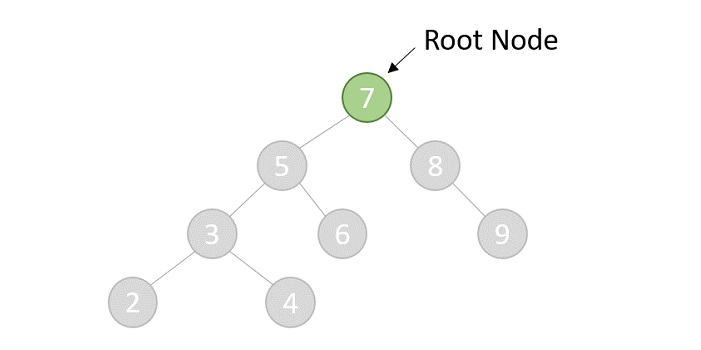
Zig-Zig rotation

The zig-zig rotations are performed when the operational node has both parent and a grandparent. The node is rotated two places towards its right.

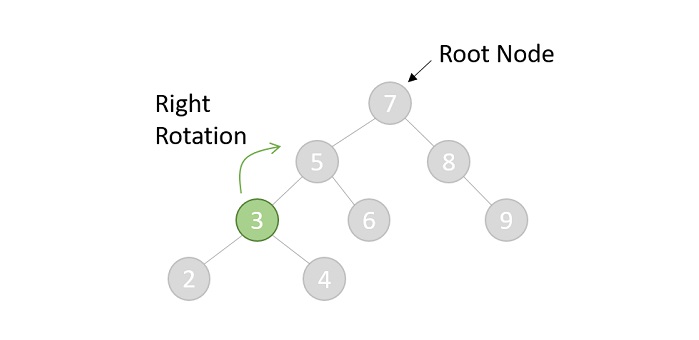
The first rotation will shift the tree to one position right −

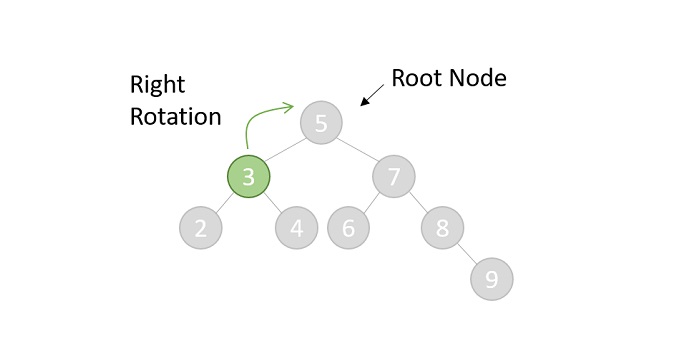
The second right rotation will once again shift the node for one position. The final tree after the shift will look like this −

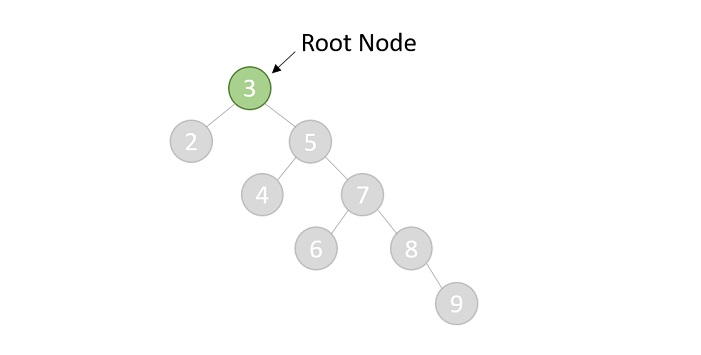
Zag-Zag rotation

The zag-zag rotations are also performed when the operational node has both parent and a grandparent. The node is rotated two places towards its left.

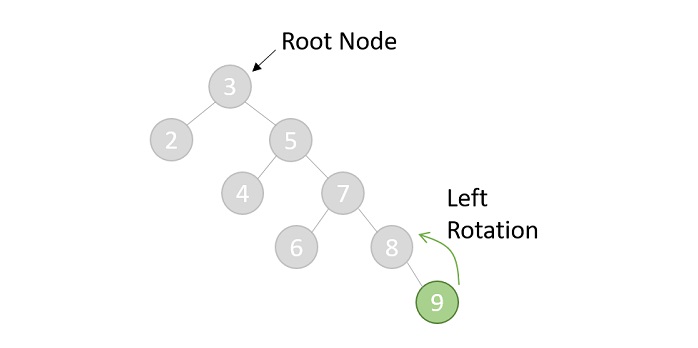
After the first rotation, the tree will look like −

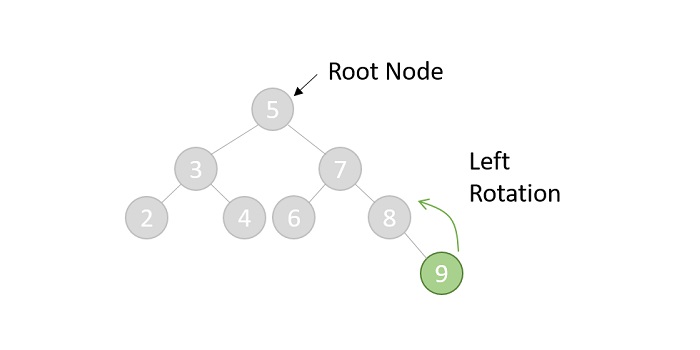
Then the final tree after the second rotation is given as follows. However, the operational node is still not the root so the splaying is considered incomplete. Hence, other suitable rotations are again applied in this case until the node becomes the root.

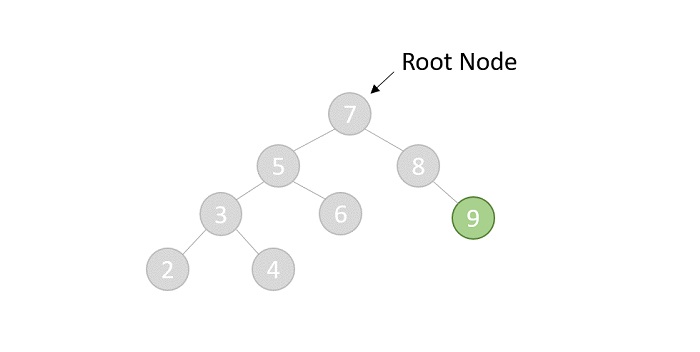
Zig-Zag rotation

The zig-zag rotations are performed when the operational node has both a parent and a grandparent. But the difference is the grandparent, parent and child are in LRL format. The node is rotated first towards its right followed by left.

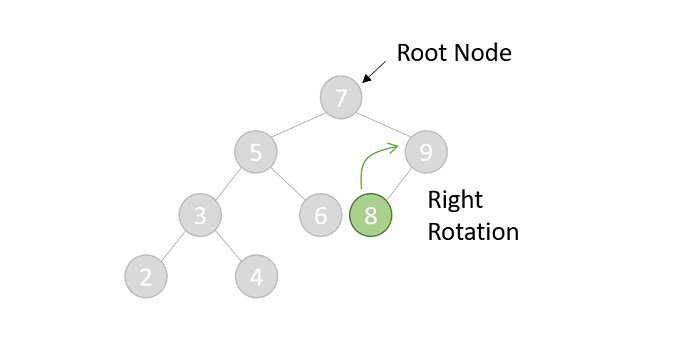
After the first rotation, the tree is −

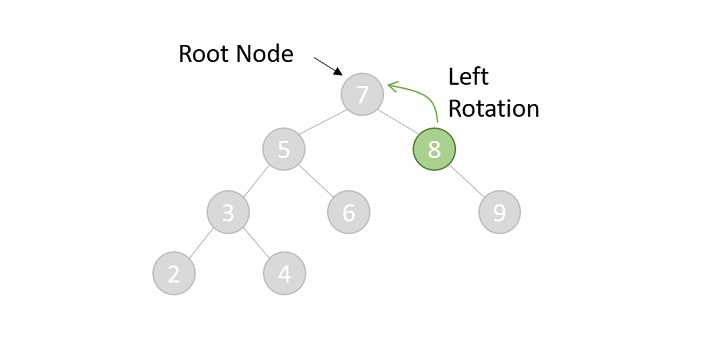
The final tree after the second rotation −

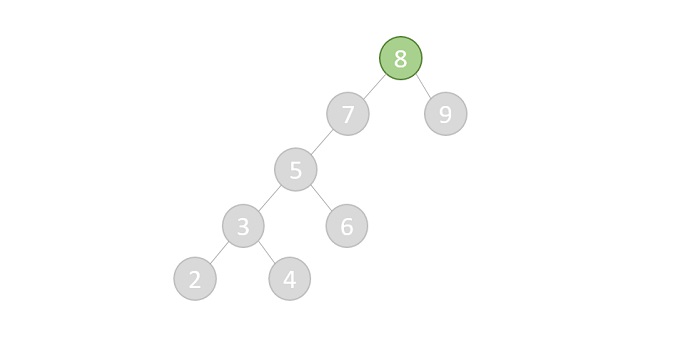
Zag-Zig rotation

The zag-zig rotations are also performed when the operational node has both parent and grandparent. But the difference is the grandparent, parent and child are in RLR format. The node is rotated first towards its left followed by right.

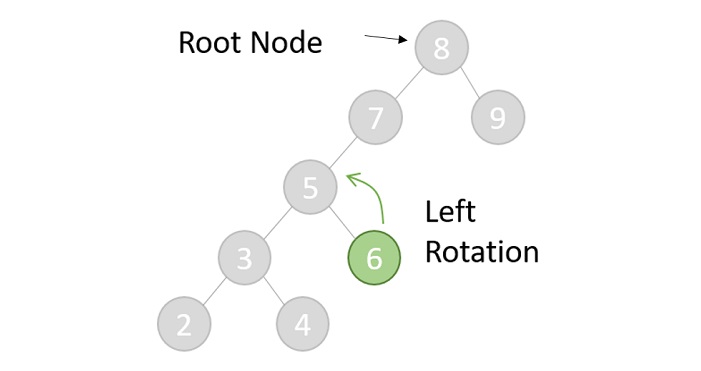
First rotation is performed, the tree is obtained as −

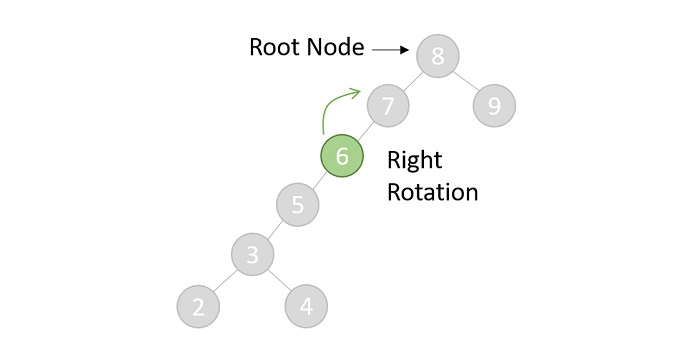
After second rotation, the final tree is given as below. However, the operational node is not the root node yet so one more rotation needs to be performed to make the said node as the root.

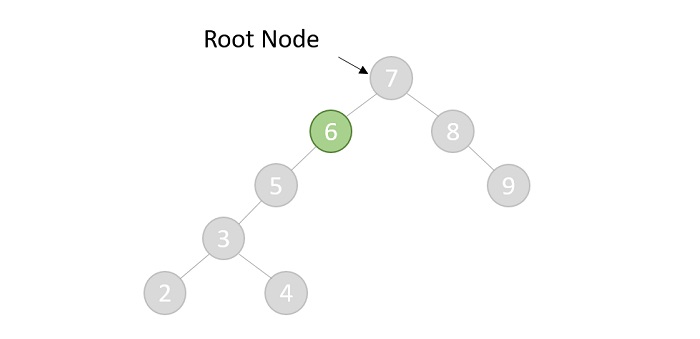
Basic Operations of Splay Trees

A splay contains the same basic operations that a Binary Search Tree provides with: Insertion, Deletion, and Search. However, after every operation there is an additional operation that differs them from Binary Search tree operations: Splaying. We have learned about Splaying already so let us understand the procedures of the other operations.

Insertion

The insertion operation in a Splay tree is performed in the exact same way insertion in a binary search tree is performed. The procedure to perform the insertion in a splay tree is given as follows −

Check whether the tree is empty; if yes, add the new node and exit

If the tree is not empty, add the new node to the existing tree using the binary search insertion.

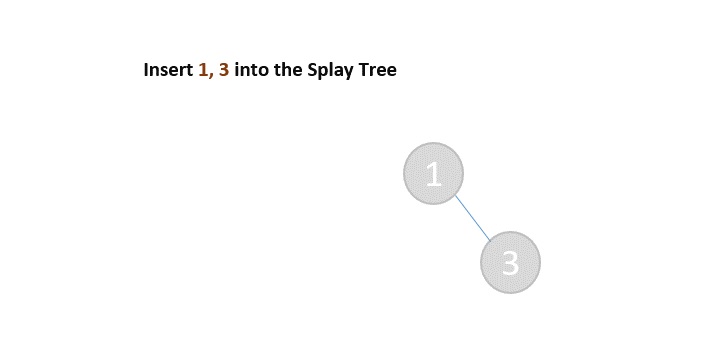
Then, suitable splaying is chosen and applied on the newly added node.

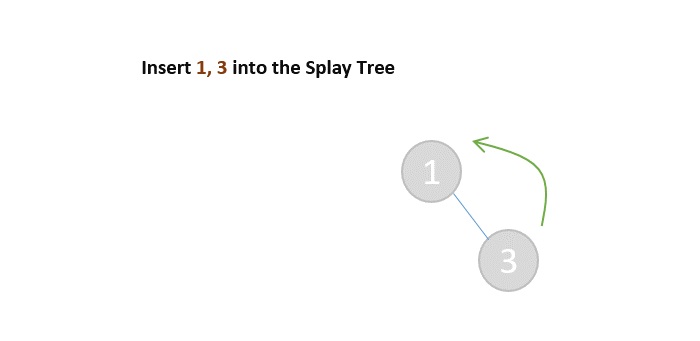
Zag (Left) Rotation is applied on the new node

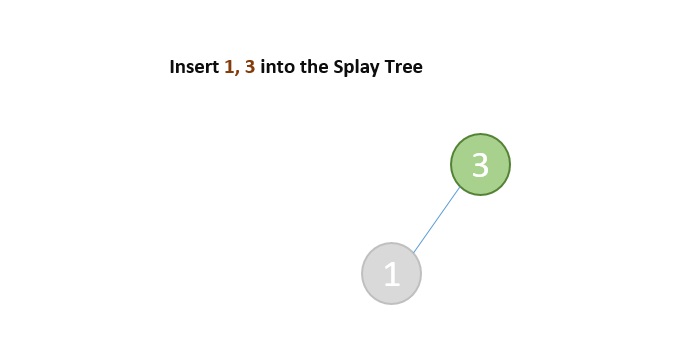
Example

Following are the implementations of this operation in various programming languages −

C C++ Java

#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild, *rightChild;
};
struct node* newNode(int data){
   struct node* Node = (struct node*)malloc(sizeof(struct node));
   Node->data = data;
   Node->leftChild = Node->rightChild = NULL;
   return (Node);
}
struct node* rightRotate(struct node *x){
   struct node *y = x->leftChild;
   x->leftChild = y->rightChild;
   y->rightChild = x;
   return y;
}
struct node* leftRotate(struct node *x){
   struct node *y = x->rightChild;
   x->rightChild = y->leftChild;
   y->leftChild = x;
   return y;
}
struct node* splay(struct node *root, int data){
   if (root == NULL || root->data == data)
      return root;
   if (root->data > data) {
      if (root->leftChild == NULL) return root;
      if (root->leftChild->data > data) {
         root->leftChild->leftChild = splay(root->leftChild->leftChild, data);
         root = rightRotate(root);
      } else if (root->leftChild->data < data) {
         root->leftChild->rightChild = splay(root->leftChild->rightChild, data);
         if (root->leftChild->rightChild != NULL)
            root->leftChild = leftRotate(root->leftChild);
      }
      return (root->leftChild == NULL)? root: rightRotate(root);
   } else {
      if (root->rightChild == NULL) return root;
      if (root->rightChild->data > data) {
         root->rightChild->leftChild = splay(root->rightChild->leftChild, data);
         if (root->rightChild->leftChild != NULL)
            root->rightChild = rightRotate(root->rightChild);
      } else if (root->rightChild->data < data) {
         root->rightChild->rightChild = splay(root->rightChild->rightChild, data);
         root = leftRotate(root);
      }
      return (root->rightChild == NULL)? root: leftRotate(root);
   }
}
struct node* insert(struct node *root, int k){
   if (root == NULL) return newNode(k);
   root = splay(root, k);
   if (root->data == k) return root;
   struct node *newnode = newNode(k);
   if (root->data > k) {
      newnode->rightChild = root;
      newnode->leftChild = root->leftChild;
      root->leftChild = NULL;
   } else {
      newnode->leftChild = root;
      newnode->rightChild = root->rightChild;
      root->rightChild = NULL;
   }
   return newnode;
}
void printTree(struct node *root){
   if (root == NULL)
      return;
   if (root != NULL) {
      printTree(root->leftChild);
      printf("%d ", root->data);
      printTree(root->rightChild);
   }
}
int main(){
   struct node* root = newNode(34);
   root->leftChild = newNode(15);
   root->rightChild = newNode(40);
   root->leftChild->leftChild = newNode(12);
   root->leftChild->leftChild->rightChild = newNode(14);
   root->rightChild->rightChild = newNode(59);
   printf("The Splay tree is \n");
   printTree(root);
   return 0;
}

#include <iostream>
struct node {
   int data;
   struct node *leftChild, *rightChild;
};
struct node* newNode(int data){
   struct node* Node = (struct node*)malloc(sizeof(struct node));
   Node->data = data;
   Node->leftChild = Node->rightChild = NULL;
   return (Node);
}
struct node* rightRotate(struct node *x){
   struct node *y = x->leftChild;
   x->leftChild = y->rightChild;
   y->rightChild = x;
   return y;
}
struct node* leftRotate(struct node *x){
   struct node *y = x->rightChild;
   x->rightChild = y->leftChild;
   y->leftChild = x;
   return y;
}
struct node* splay(struct node *root, int data){
   if (root == NULL || root->data == data)
      return root;
   if (root->data > data) {
      if (root->leftChild == NULL) return root;
      if (root->leftChild->data > data) {
         root->leftChild->leftChild = splay(root->leftChild->leftChild, data);
         root = rightRotate(root);
      } else if (root->leftChild->data < data) {
         root->leftChild->rightChild = splay(root->leftChild->rightChild, data);
         if (root->leftChild->rightChild != NULL)
            root->leftChild = leftRotate(root->leftChild);
      }
      return (root->leftChild == NULL)? root: rightRotate(root);
   } else {
      if (root->rightChild == NULL) return root;
      if (root->rightChild->data > data) {
         root->rightChild->leftChild = splay(root->rightChild->leftChild, data);
         if (root->rightChild->leftChild != NULL)
            root->rightChild = rightRotate(root->rightChild);
      } else if (root->rightChild->data < data) {
         root->rightChild->rightChild = splay(root->rightChild->rightChild, data);
         root = leftRotate(root);
      }
      return (root->rightChild == NULL)? root: leftRotate(root);
   }
}
struct node* insert(struct node *root, int k){
   if (root == NULL) return newNode(k);
   root = splay(root, k);
   if (root->data == k) return root;
   struct node *newnode = newNode(k);
   if (root->data > k) {
      newnode->rightChild = root;
      newnode->leftChild = root->leftChild;
      root->leftChild = NULL;
   } else {
      newnode->leftChild = root;
      newnode->rightChild = root->rightChild;
      root->rightChild = NULL;
   }
   return newnode;
}
void printTree(struct node *root){
   if (root == NULL)
      return;
   if (root != NULL) {
      printTree(root->leftChild);
      printf("%d ", root->data);
      printTree(root->rightChild);
   }
}
int main(){
   struct node* root = newNode(34);
   root->leftChild = newNode(15);
   root->rightChild = newNode(40);
   root->leftChild->leftChild = newNode(12);
   root->leftChild->leftChild->rightChild = newNode(14);
   root->rightChild->rightChild = newNode(59);
   printf("The Splay tree is \n");
   printTree(root);
   return 0;
}

import java.io.*;
public class SplayTree {
   static class node {
      int data;
      node leftChild, rightChild;
   };
   static node newNode(int data) {
      node Node = new node();
      Node.data = data;
      Node.leftChild = Node.rightChild = null;
      return (Node);
   }
   static node rightRotate(node x) {
      node y = x.leftChild;
      x.leftChild = y.rightChild;
      y.rightChild = x;
      return y;
   }
   static node leftRotate(node x) {
      node y = x.rightChild;
      x.rightChild = y.leftChild;
      y.leftChild = x;
      return y;
   }
   static node splay(node root, int data) {
      if (root == null || root.data == data)
         return root;
      if (root.data > data) {
         if (root.leftChild == null) return root;
         if (root.leftChild.data > data) {
            root.leftChild.leftChild = splay(root.leftChild.leftChild, data);
            root = rightRotate(root);
         } else if (root.leftChild.data < data) {
            root.leftChild.rightChild = splay(root.leftChild.rightChild, data);
            if (root.leftChild.rightChild != null)
               root.leftChild = leftRotate(root.leftChild);
         }
         return (root.leftChild == null)? root: rightRotate(root);
      } else {
         if (root.rightChild == null) return root;
         if (root.rightChild.data > data) {
            root.rightChild.leftChild = splay(root.rightChild.leftChild, data);
            if (root.rightChild.leftChild != null)
               root.rightChild = rightRotate(root.rightChild);
         } else if (root.rightChild.data < data) {
            root.rightChild.rightChild = splay(root.rightChild.rightChild, data);
            root = leftRotate(root);
         }
         return (root.rightChild == null)? root: leftRotate(root);
      }
   }
   static node insert(node root, int k) {
      if (root == null) return newNode(k);
      root = splay(root, k);
      if (root.data == k) return root;
      node newnode = newNode(k);
      if (root.data > k) {
         newnode.rightChild = root;
         newnode.leftChild = root.leftChild;
         root.leftChild = null;
      } else {
         newnode.leftChild = root;
         newnode.rightChild = root.rightChild;
         root.rightChild = null;
      }
      return newnode;
   }
   static void printTree(node root) {
      if (root == null)
         return;
      if (root != null) {
         printTree(root.leftChild);
         System.out.print(root.data + " ");
         printTree(root.rightChild);
      }
   }
   public static void main(String args[]) {
      node root = newNode(34);
      root.leftChild = newNode(15);
      root.rightChild = newNode(40);
      root.leftChild.leftChild = newNode(12);
      root.leftChild.leftChild.rightChild = newNode(14);
      root.rightChild.rightChild = newNode(59);
      System.out.println("The Splay tree is: ");
      printTree(root);
   }
}

Deletion

The deletion operation in a splay tree is performed as following −

Apply splaying operation on the node to be deleted.
Once, the node is made the root, delete the node.
Now, the tree is split into two trees, the left subtree and the right subtree; with their respective first nodes as the root nodes: say root_left and root_right.

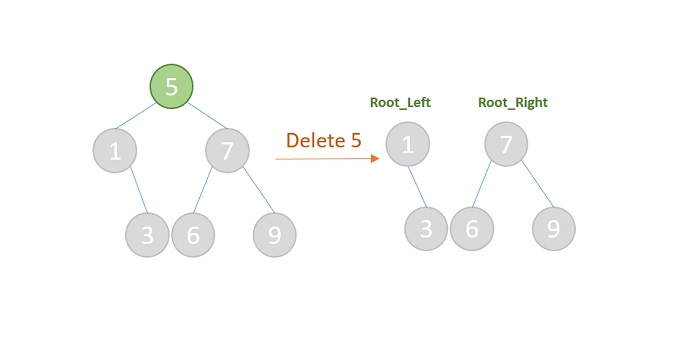
If root_left is a NULL value, then the root_right will become the root of the tree. And vice versa.
But if both root_left and root_right are not NULL values, then select the maximum value from the left subtree and make it the new root by connecting the subtrees.

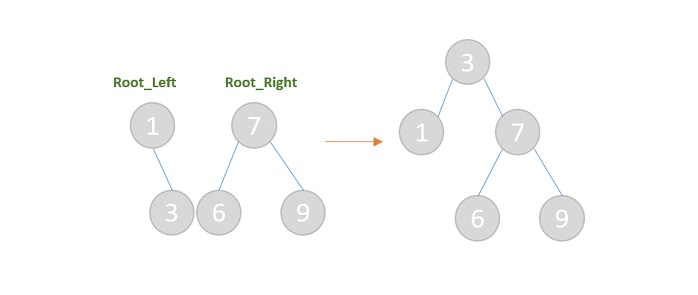
Example

Following are the implementations of this operation in various programming languages −

C C++ Java

#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild, *rightChild;
};
struct node* newNode(int data){
   struct node* Node = (struct node*)malloc(sizeof(struct node));
   Node->data = data;
   Node->leftChild = Node->rightChild = NULL;
   return (Node);
}
struct node* rightRotate(struct node *x){
   struct node *y = x->leftChild;
   x->leftChild = y->rightChild;
   y->rightChild = x;
   return y;
}
struct node* leftRotate(struct node *x){
   struct node *y = x->rightChild;
   x->rightChild = y->leftChild;
   y->leftChild = x;
   return y;
}
struct node* splay(struct node *root, int data){
   if (root == NULL || root->data == data)
      return root;
   if (root->data > data) {
      if (root->leftChild == NULL) return root;
      if (root->leftChild->data > data) {
         root->leftChild->leftChild = splay(root->leftChild->leftChild, data);
         root = rightRotate(root);
      } else if (root->leftChild->data < data) {
         root->leftChild->rightChild = splay(root->leftChild->rightChild, data);
         if (root->leftChild->rightChild != NULL)
            root->leftChild = leftRotate(root->leftChild);
      }
      return (root->leftChild == NULL)? root: rightRotate(root);
   } else {
      if (root->rightChild == NULL) return root;
      if (root->rightChild->data > data) {
         root->rightChild->leftChild = splay(root->rightChild->leftChild, data);
         if (root->rightChild->leftChild != NULL)
            root->rightChild = rightRotate(root->rightChild);
      } else if (root->rightChild->data < data) {
         root->rightChild->rightChild = splay(root->rightChild->rightChild, data);
         root = leftRotate(root);
      }
      return (root->rightChild == NULL)? root: leftRotate(root);
   }
}
struct node* insert(struct node *root, int k){
   if (root == NULL) return newNode(k);
   root = splay(root, k);
   if (root->data == k) return root;
   struct node *newnode = newNode(k);
   if (root->data > k) {
      newnode->rightChild = root;
      newnode->leftChild = root->leftChild;
      root->leftChild = NULL;
   } else {
      newnode->leftChild = root;
      newnode->rightChild = root->rightChild;
      root->rightChild = NULL;
   }
   return newnode;
}
struct node* deletenode(struct node* root, int data){
   struct node* temp;
   if (root == NULL)
      return NULL;
   root = splay(root, data);
   if (data != root->data)
      return root;
   if (!root->leftChild) {
      temp = root;
      root = root->rightChild;
   } else {
      temp = root;
      root = splay(root->leftChild, data);
      root->rightChild = temp->rightChild;
   }
   free(temp);
   return root;
}
void printTree(struct node *root){
   if (root == NULL)
      return;
   if (root != NULL) {
      printTree(root->leftChild);
      printf("%d ", root->data);
      printTree(root->rightChild);
   }
}
int main(){
   struct node* root = newNode(34);
   root->leftChild = newNode(15);
   root->rightChild = newNode(40);
   printf("The Splay tree is \n");
   printTree(root);
   root = deletenode(root, 40);
   printf("\nThe Splay tree after deletion is \n");
   printTree(root);
   return 0;
}

#include <iostream>
struct node {
   int data;
   struct node *leftChild, *rightChild;
};
struct node* newNode(int data){
   struct node* Node = (struct node*)malloc(sizeof(struct node));
   Node->data = data;
   Node->leftChild = Node->rightChild = NULL;
   return (Node);
}
struct node* rightRotate(struct node *x){
   struct node *y = x->leftChild;
   x->leftChild = y->rightChild;
   y->rightChild = x;
   return y;
}
struct node* leftRotate(struct node *x){
   struct node *y = x->rightChild;
   x->rightChild = y->leftChild;
   y->leftChild = x;
   return y;
}
struct node* splay(struct node *root, int data){
   if (root == NULL || root->data == data)
      return root;
   if (root->data > data) {
      if (root->leftChild == NULL) return root;
      if (root->leftChild->data > data) {
         root->leftChild->leftChild = splay(root->leftChild->leftChild, data);
         root = rightRotate(root);
      } else if (root->leftChild->data < data) {
         root->leftChild->rightChild = splay(root->leftChild->rightChild, data);
         if (root->leftChild->rightChild != NULL)
            root->leftChild = leftRotate(root->leftChild);
      }
      return (root->leftChild == NULL)? root: rightRotate(root);
   } else {
      if (root->rightChild == NULL) return root;
      if (root->rightChild->data > data) {
         root->rightChild->leftChild = splay(root->rightChild->leftChild, data);
         if (root->rightChild->leftChild != NULL)
            root->rightChild = rightRotate(root->rightChild);
      } else if (root->rightChild->data < data) {
         root->rightChild->rightChild = splay(root->rightChild->rightChild, data);
         root = leftRotate(root);
      }
      return (root->rightChild == NULL)? root: leftRotate(root);
   }
}
struct node* insert(struct node *root, int k){
   if (root == NULL) return newNode(k);
   root = splay(root, k);
   if (root->data == k) return root;
   struct node *newnode = newNode(k);
   if (root->data > k) {
      newnode->rightChild = root;
      newnode->leftChild = root->leftChild;
      root->leftChild = NULL;
   } else {
      newnode->leftChild = root;
      newnode->rightChild = root->rightChild;
      root->rightChild = NULL;
   }
   return newnode;
}
struct node* deletenode(struct node* root, int data){
   struct node* temp;
   if (root == NULL)
      return NULL;
   root = splay(root, data);
   if (data != root->data)
      return root;
   if (!root->leftChild) {
      temp = root;
      root = root->rightChild;
   } else {
      temp = root;
      root = splay(root->leftChild, data);
      root->rightChild = temp->rightChild;
   }
   free(temp);
   return root;
}
void printTree(struct node *root){
   if (root == NULL)
      return;
   if (root != NULL) {
      printTree(root->leftChild);
      printf("%d ", root->data);
      printTree(root->rightChild);
   }
}
int main(){
   struct node* root = newNode(34);
   root->leftChild = newNode(15);
   root->rightChild = newNode(40);
   printf("The Splay tree is \n");
   printTree(root);
   root = deletenode(root, 40);
   printf("\nThe Splay tree after deletion is \n");
   printTree(root);
   return 0;
}

import java.io.*;
public class SplayTree {
   static class node {
      int data;
      node leftChild, rightChild;
   };
   static node newNode(int data) {
      node Node = new node();
      Node.data = data;
      Node.leftChild = Node.rightChild = null;
      return (Node);
   }
   static node rightRotate(node x) {
      node y = x.leftChild;
      x.leftChild = y.rightChild;
      y.rightChild = x;
      return y;
   }
   static node leftRotate(node x) {
      node y = x.rightChild;
      x.rightChild = y.leftChild;
      y.leftChild = x;
      return y;
   }
   static node splay(node root, int data) {
      if (root == null || root.data == data)
         return root;
      if (root.data > data) {
         if (root.leftChild == null) return root;
         if (root.leftChild.data > data) {
            root.leftChild.leftChild = splay(root.leftChild.leftChild, data);
            root = rightRotate(root);
         } else if (root.leftChild.data < data) {
            root.leftChild.rightChild = splay(root.leftChild.rightChild, data);
            if (root.leftChild.rightChild != null)
               root.leftChild = leftRotate(root.leftChild);
         }
         return (root.leftChild == null)? root: rightRotate(root);
      } else {
         if (root.rightChild == null) return root;
         if (root.rightChild.data > data) {
            root.rightChild.leftChild = splay(root.rightChild.leftChild, data);
            if (root.rightChild.leftChild != null)
               root.rightChild = rightRotate(root.rightChild);
         } else if (root.rightChild.data < data) {
            root.rightChild.rightChild = splay(root.rightChild.rightChild, data);
            root = leftRotate(root);
         }
         return (root.rightChild == null)? root: leftRotate(root);
      }
   }
   static node insert(node root, int k) {
      if (root == null) return newNode(k);
      root = splay(root, k);
      if (root.data == k) return root;
      node newnode = newNode(k);
      if (root.data > k) {
         newnode.rightChild = root;
         newnode.leftChild = root.leftChild;
         root.leftChild = null;
      } else {
         newnode.leftChild = root;
         newnode.rightChild = root.rightChild;
         root.rightChild = null;
      }
      return newnode;
   }
   static node deletenode(node root, int data) {
      node temp;
      if (root == null)
         return null;
      root = splay(root, data);
      if (data != root.data)
         return root;
      if (root.leftChild == null) {
         temp = root;
         root = root.rightChild;
      } else {
         temp = root;
         root = splay(root.leftChild, data);
         root.rightChild = temp.rightChild;
      }
      return root;
   }
   static void printTree(node root) {
      if (root == null)
         return;
      if (root != null) {
         printTree(root.leftChild);
         System.out.print(root.data + " ");
         printTree(root.rightChild);
      }
   }
   public static void main(String args[]) {
      node root = newNode(34);
      root.leftChild = newNode(15);
      root.rightChild = newNode(40);
      System.out.println("The Splay tree is: ");
      printTree(root);
      root = deletenode(root, 40);
      System.out.println("\nThe Splay tree after deletion is: ");
      printTree(root);
   }
}

Search

The search operation in a Splay tree follows the same procedure of the Binary Search Tree operation. However, after the searching is done and the element is found, splaying is applied on the node searched. If the element is not found, then unsuccessful search is prompted.

Example

Following are the implementations of this operation in various programming languages −

C C++ Java

#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild, *rightChild;
};
struct node* newNode(int data){
   struct node* Node = (struct node*)malloc(sizeof(struct node));
   Node->data = data;
   Node->leftChild = Node->rightChild = NULL;
   return (Node);
}
struct node* rightRotate(struct node *x){
   struct node *y = x->leftChild;
   x->leftChild = y->rightChild;
   y->rightChild = x;
   return y;
}
struct node* leftRotate(struct node *x){
   struct node *y = x->rightChild;
   x->rightChild = y->leftChild;
   y->leftChild = x;
   return y;
}
struct node* splay(struct node *root, int data){
   if (root == NULL || root->data == data)
      return root;
   if (root->data > data) {
      if (root->leftChild == NULL) return root;
      if (root->leftChild->data > data) {
         root->leftChild->leftChild = splay(root->leftChild->leftChild, data);
         root = rightRotate(root);
      } else if (root->leftChild->data < data) {
         root->leftChild->rightChild = splay(root->leftChild->rightChild, data);
         if (root->leftChild->rightChild != NULL)
            root->leftChild = leftRotate(root->leftChild);
      }
      return (root->leftChild == NULL)? root: rightRotate(root);
   } else {
      if (root->rightChild == NULL) return root;
      if (root->rightChild->data > data) {
         root->rightChild->leftChild = splay(root->rightChild->leftChild, data);
         if (root->rightChild->leftChild != NULL)
            root->rightChild = rightRotate(root->rightChild);
      } else if (root->rightChild->data < data) {
         root->rightChild->rightChild = splay(root->rightChild->rightChild, data);
         root = leftRotate(root);
      }
      return (root->rightChild == NULL)? root: leftRotate(root);
   }
}
struct node* insert(struct node *root, int k){
   if (root == NULL) return newNode(k);
   root = splay(root, k);
   if (root->data == k) return root;
   struct node *newnode = newNode(k);
   if (root->data > k) {
      newnode->rightChild = root;
      newnode->leftChild = root->leftChild;
      root->leftChild = NULL;
   } else {
      newnode->leftChild = root;
      newnode->rightChild = root->rightChild;
      root->rightChild = NULL;
   }
   return newnode;
}
struct node* deletenode(struct node* root, int data){
   struct node* temp;
   if (root == NULL)
      return NULL;
   root = splay(root, data);
   if (data != root->data)
      return root;
   if (!root->leftChild) {
      temp = root;
      root = root->rightChild;
   } else {
      temp = root;
      root = splay(root->leftChild, data);
      root->rightChild = temp->rightChild;
   }
   free(temp);
   return root;
}
void printTree(struct node *root){
   if (root == NULL)
      return;
   if (root != NULL) {
      printTree(root->leftChild);
      printf("%d ", root->data);
      printTree(root->rightChild);
   }
}
int main(){
   struct node* root = newNode(34);
   root->leftChild = newNode(15);
   root->rightChild = newNode(40);
   root->leftChild->leftChild = newNode(12);
   root->leftChild->leftChild->rightChild = newNode(14);
   root->rightChild->rightChild = newNode(59);
   printf("The Splay tree is \n");
   printTree(root);
   root = deletenode(root, 40);
   printf("\nThe Splay tree after deletion is \n");
   printTree(root);
   return 0;
}

#include <bits/stdc++.h>
using namespace std;
class node{
public:
   int data;
   node *leftChild, *rightChild;
};
node* newNode(int data){
   node* Node = new node();
   Node->data = data;
   Node->leftChild = Node->rightChild = NULL;
   return (Node);
}
node *rightRotate(node *x){
   node *y = x->leftChild;
   x->leftChild = y->rightChild;
   y->rightChild = x;
   return y;
}
node *leftRotate(node *x){
   node *y = x->rightChild;
   x->rightChild = y->leftChild;
   y->leftChild = x;
   return y;
}
node *splay(node *root, int data){
   if (root == NULL || root->data == data)
      return root;
   if (root->data > data) {
      if (root->leftChild == NULL) return root;
      if (root->leftChild->data > data) {
         root->leftChild->leftChild = splay(root->leftChild->leftChild, data);
         root = rightRotate(root);
      } else if (root->leftChild->data < data) {
         root->leftChild->rightChild = splay(root->leftChild->rightChild, data);
         if (root->leftChild->rightChild != NULL)
            root->leftChild = leftRotate(root->leftChild);
      }
      return (root->leftChild == NULL)? root: rightRotate(root);
   } else {
      if (root->rightChild == NULL) return root;
      if (root->rightChild->data > data) {
         root->rightChild->leftChild = splay(root->rightChild->leftChild, data);
         if (root->rightChild->leftChild != NULL)
            root->rightChild = rightRotate(root->rightChild);
      } else if (root->rightChild->data < data) {
         root->rightChild->rightChild = splay(root->rightChild->rightChild, data);
         root = leftRotate(root);
      }
      return (root->rightChild == NULL)? root: leftRotate(root);
   }
}
node* insert(node *root, int k)
{
   if (root == NULL) return newNode(k);
   root = splay(root, k);
   if (root->data == k) return root;
   node *newnode = newNode(k);
   if (root->data > k) {
      newnode->rightChild = root;
      newnode->leftChild = root->leftChild;
      root->leftChild = NULL;
   } else {
      newnode->leftChild = root;
      newnode->rightChild = root->rightChild;
      root->rightChild = NULL;
   }
   return newnode;
}
node* deletenode(struct node* root, int data){
   struct node* temp;
   if (root == NULL)
      return NULL;
   root = splay(root, data);
   if (data != root->data)
      return root;
   if (!root->leftChild) {
      temp = root;
      root = root->rightChild;
   } else {
      temp = root;
      root = splay(root->leftChild, data);
      root->rightChild = temp->rightChild;
   }
   free(temp);
   return root;
}
void printTree(node *root){
   if (root == NULL)
      return;
   if (root != NULL) {
      printTree(root->leftChild);
      cout<<root->data<<" ";
      printTree(root->rightChild);
   }
}
int main(){
   node* root = newNode(34);
   root->leftChild = newNode(15);
   root->rightChild = newNode(40);
   root->leftChild->leftChild = newNode(12);
   root->leftChild->leftChild->rightChild = newNode(14);
   root->rightChild->rightChild = newNode(59);
   cout<<"The Splay tree is \n";
   printTree(root);
   root = deletenode(root, 40);
   cout<<"\nThe Splay tree after deletion is \n";
   printTree(root);
   return 0;
}

import java.io.*;
public class SplayTree {
   static class node {
      int data;
      node leftChild, rightChild;
   };
   static node newNode(int data) {
      node Node = new node();
      Node.data = data;
      Node.leftChild = Node.rightChild = null;
      return (Node);
   }
   static node rightRotate(node x) {
      node y = x.leftChild;
      x.leftChild = y.rightChild;
      y.rightChild = x;
      return y;
   }
   static node leftRotate(node x) {
      node y = x.rightChild;
      x.rightChild = y.leftChild;
      y.leftChild = x;
      return y;
   }
   static node splay(node root, int data) {
      if (root == null || root.data == data)
         return root;
      if (root.data > data) {
         if (root.leftChild == null) return root;
         if (root.leftChild.data > data) {
            root.leftChild.leftChild = splay(root.leftChild.leftChild, data);
            root = rightRotate(root);
         } else if (root.leftChild.data < data) {
            root.leftChild.rightChild = splay(root.leftChild.rightChild, data);
            if (root.leftChild.rightChild != null)
               root.leftChild = leftRotate(root.leftChild);
         }
         return (root.leftChild == null)? root: rightRotate(root);
      } else {
         if (root.rightChild == null) return root;
         if (root.rightChild.data > data) {
            root.rightChild.leftChild = splay(root.rightChild.leftChild, data);
            if (root.rightChild.leftChild != null)
               root.rightChild = rightRotate(root.rightChild);
         } else if (root.rightChild.data < data) {
            root.rightChild.rightChild = splay(root.rightChild.rightChild, data);
            root = leftRotate(root);
         }
         return (root.rightChild == null)? root: leftRotate(root);
      }
   }
   static node insert(node root, int k) {
      if (root == null) return newNode(k);
      root = splay(root, k);
      if (root.data == k) return root;
      node newnode = newNode(k);
      if (root.data > k) {
         newnode.rightChild = root;
         newnode.leftChild = root.leftChild;
         root.leftChild = null;
      } else {
         newnode.leftChild = root;
         newnode.rightChild = root.rightChild;
         root.rightChild = null;
      }
      return newnode;
   }
   static node deletenode(node root, int data) {
      node temp;
      if (root == null)
         return null;
      root = splay(root, data);
      if (data != root.data)
         return root;
      if (root.leftChild == null) {
         temp = root;
         root = root.rightChild;
      } else {
         temp = root;
         root = splay(root.leftChild, data);
         root.rightChild = temp.rightChild;
      }
      return root;
   }
   static void printTree(node root) {
      if (root == null)
         return;
      if (root != null) {
         printTree(root.leftChild);
         System.out.print(root.data + " ");
         printTree(root.rightChild);
      }
   }
   public static void main(String args[]) {
      node root = newNode(34);
      root.leftChild = newNode(15);
      root.rightChild = newNode(40);
      root.leftChild.leftChild = newNode(12);
      root.leftChild.leftChild.rightChild = newNode(14);
      root.rightChild.rightChild = newNode(59);
      System.out.println("The Splay tree is: ");
      printTree(root);
      root = deletenode(root, 40);
      System.out.println("\nThe Splay tree after deletion is: ");
      printTree(root);
   }
}

Data Structure & Algorithms - Spanning Tree

A spanning tree is a subset of Graph G, which has all the vertices covered with minimum possible number of edges. Hence, a spanning tree does not have cycles and it cannot be disconnected..

By this definition, we can draw a conclusion that every connected and undirected Graph G has at least one spanning tree. A disconnected graph does not have any spanning tree, as it cannot be spanned to all its vertices.

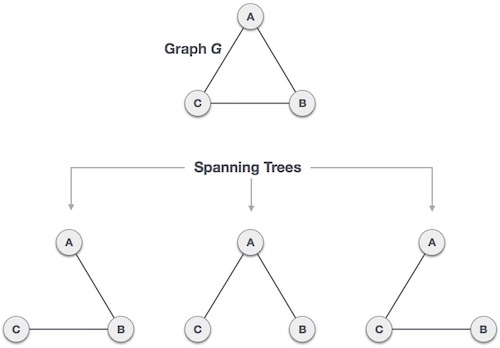
We found three spanning trees off one complete graph. A complete undirected graph can have maximum n^n-2 number of spanning trees, where n is the number of nodes. In the above addressed example, n is 3, hence 3³⁻² = 3 spanning trees are possible.

General Properties of Spanning Tree

We now understand that one graph can have more than one spanning tree. Following are a few properties of the spanning tree connected to graph G −

A connected graph G can have more than one spanning tree.
All possible spanning trees of graph G, have the same number of edges and vertices.
The spanning tree does not have any cycle (loops).
Removing one edge from the spanning tree will make the graph disconnected, i.e. the spanning tree is minimally connected.
Adding one edge to the spanning tree will create a circuit or loop, i.e. the spanning tree is maximally acyclic.

Mathematical Properties of Spanning Tree

Spanning tree has n-1 edges, where n is the number of nodes (vertices).
From a complete graph, by removing maximum e - n + 1 edges, we can construct a spanning tree.
A complete graph can have maximum n^n-2 number of spanning trees.

Thus, we can conclude that spanning trees are a subset of connected Graph G and disconnected graphs do not have spanning tree.

Application of Spanning Tree

Spanning tree is basically used to find a minimum path to connect all nodes in a graph. Common application of spanning trees are −

Civil Network Planning
Computer Network Routing Protocol
Cluster Analysis

Let us understand this through a small example. Consider, city network as a huge graph and now plans to deploy telephone lines in such a way that in minimum lines we can connect to all city nodes. This is where the spanning tree comes into picture.

Minimum Spanning Tree (MST)

In a weighted graph, a minimum spanning tree is a spanning tree that has minimum weight than all other spanning trees of the same graph. In real-world situations, this weight can be measured as distance, congestion, traffic load or any arbitrary value denoted to the edges.

Minimum Spanning-Tree Algorithm

We shall learn about two most important spanning tree algorithms here −

Both are greedy algorithms.

Data Structure and Algorithms - Tries

A trie is a type of a multi-way search tree, which is fundamentally used to retrieve specific keys from a string or a set of strings. It stores the data in an ordered efficient way since it uses pointers to every letter within the alphabet.

The trie data structure works based on the common prefixes of strings. The root node can have any number of nodes considering the amount of strings present in the set. The root of a trie does not contain any value except the pointers to its child nodes.

There are three types of trie data structures −

Standard Tries
Compressed Tries
Suffix Tries

The real-world applications of trie include − autocorrect, text prediction, sentiment analysis and data sciences.

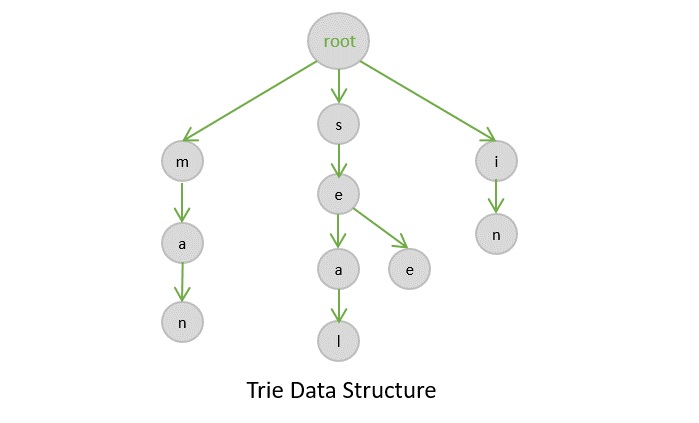
Basic Operations in Tries

The trie data structures also perform the same operations that tree data structures perform. They are −

Insertion
Deletion
Search

Insertion

The insertion operation in a trie is a simple approach. The root in a trie does not hold any value and the insertion starts from the immediate child nodes of the root, which act like a key to their child nodes. However, we observe that each node in a trie represents a singlecharacter in the input string. Hence the characters are added into the tries one by one while the links in the trie act as pointers to the next level nodes.

Deletion

The deletion operation in a trie is performed using the bottom-up approach. The element is searched for in a trie and deleted, if found. However, there are some special scenarios that need to be kept in mind while performing the deletion operation.

Case 1 − The key is unique − in this case, the entire key path is deleted from the node. (Unique key suggests that there is no other path that branches out from one path).

Case 2 − The key is not unique − the leaf nodes are updated. For example, if the key to be deleted is see but it is a prefix of another key seethe; we delete the see and change the Boolean values of t, h and e as false.

Case 3 − The key to be deleted already has a prefix − the values until the prefix are deleted and the prefix remains in the tree. For example, if the key to be deleted is heart but there is another key present he; so we delete a, r, and t until only he remains.

Search

Searching in a trie is a rather straightforward approach. We can only move down the levels of trie based on the key node (the nodes where insertion operation starts at). Searching is done until the end of the path is reached. If the element is found, search is successful; otherwise, search is prompted unsuccessful.

Heap Data Structures

Heap is a special case of balanced binary tree data structure where the root-node key is compared with its children and arranged accordingly. If α has child node β then −

key(α) ≥ key(β)

As the value of parent is greater than that of child, this property generates Max Heap. Based on this criteria, a heap can be of two types −

For Input → 35 33 42 10 14 19 27 44 26 31

Min-Heap − Where the value of the root node is less than or equal to either of its children.

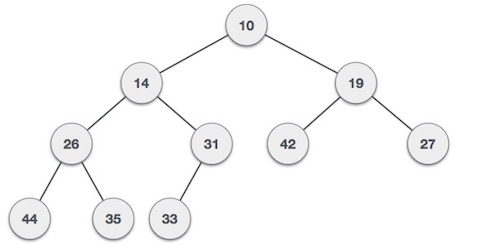
Max-Heap − Where the value of the root node is greater than or equal to either of its children.

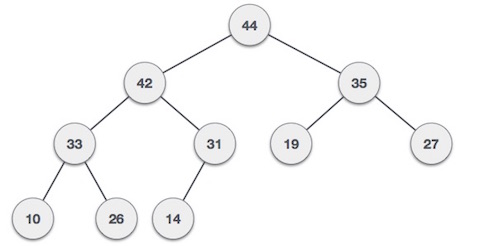
Both trees are constructed using the same input and order of arrival.

Max Heap Construction Algorithm

We shall use the same example to demonstrate how a Max Heap is created. The procedure to create Min Heap is similar but we go for min values instead of max values.

We are going to derive an algorithm for max heap by inserting one element at a time. At any point of time, heap must maintain its property. While insertion, we also assume that we are inserting a node in an already heapified tree.

Step 1 − Create a new node at the end of heap.
Step 2 − Assign new value to the node.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.

Note − In Min Heap construction algorithm, we expect the value of the parent node to be less than that of the child node.

Let's understand Max Heap construction by an animated illustration. We consider the same input sample that we used earlier.

Max Heap Deletion Algorithm

Let us derive an algorithm to delete from max heap. Deletion in Max (or Min) Heap always happens at the root to remove the Maximum (or minimum) value.

Step 1 − Remove root node.
Step 2 − Move the last element of last level to root.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.

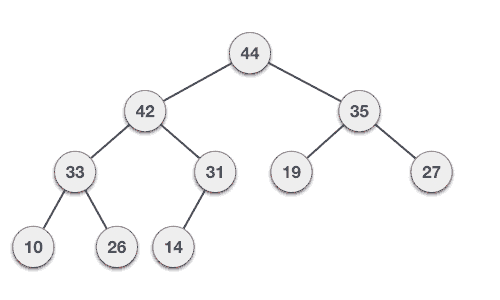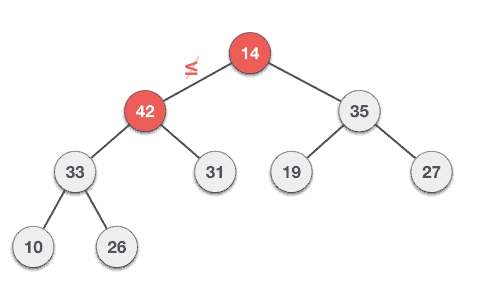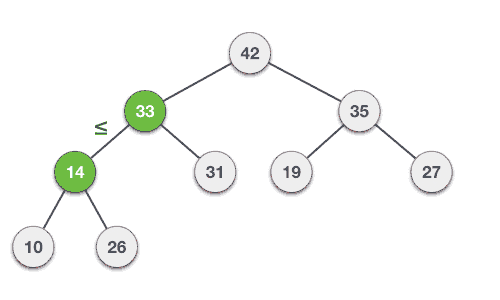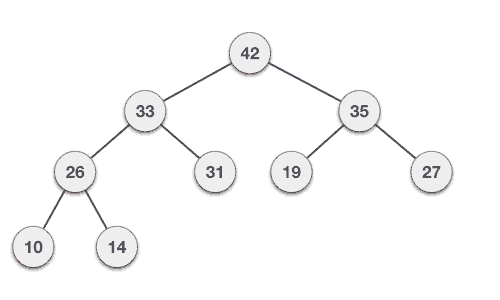
Data Structure - Recursion Basics

Some computer programming languages allow a module or function to call itself. This technique is known as recursion. In recursion, a function α either calls itself directly or calls a function β that in turn calls the original function α. The function α is called recursive function.

Example − a function calling itself.

int function(int value) {
   if(value < 1)
      return;
   function(value - 1);

   printf("%d ",value);   
}

Example − a function that calls another function which in turn calls it again.

int function1(int value1) {
   if(value1 < 1)
      return;
   function2(value1 - 1);
   printf("%d ",value1);   
}
int function2(int value2) {
   function1(value2);
}

Properties

A recursive function can go infinite like a loop. To avoid infinite running of recursive function, there are two properties that a recursive function must have −

Base criteria − There must be at least one base criteria or condition, such that, when this condition is met the function stops calling itself recursively.
Progressive approach − The recursive calls should progress in such a way that each time a recursive call is made it comes closer to the base criteria.

Implementation

Many programming languages implement recursion by means of stacks. Generally, whenever a function (caller) calls another function (callee) or itself as callee, the caller function transfers execution control to the callee. This transfer process may also involve some data to be passed from the caller to the callee.

This implies, the caller function has to suspend its execution temporarily and resume later when the execution control returns from the callee function. Here, the caller function needs to start exactly from the point of execution where it puts itself on hold. It also needs the exact same data values it was working on. For this purpose, an activation record (or stack frame) is created for the caller function.

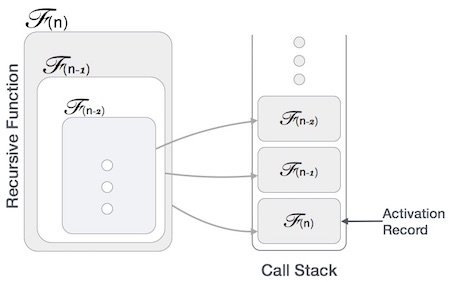
This activation record keeps the information about local variables, formal parameters, return address and all information passed to the caller function.

Analysis of Recursion

One may argue why to use recursion, as the same task can be done with iteration. The first reason is, recursion makes a program more readable and because of latest enhanced CPU systems, recursion is more efficient than iterations.

Time Complexity

In case of iterations, we take number of iterations to count the time complexity. Likewise, in case of recursion, assuming everything is constant, we try to figure out the number of times a recursive call is being made. A call made to a function is Ο(1), hence the (n) number of times a recursive call is made makes the recursive function Ο(n).

Space Complexity

Space complexity is counted as what amount of extra space is required for a module to execute. In case of iterations, the compiler hardly requires any extra space. The compiler keeps updating the values of variables used in the iterations. But in case of recursion, the system needs to store activation record each time a recursive call is made. Hence, it is considered that space complexity of recursive function may go higher than that of a function with iteration.

Data Structure & Algorithms - Tower of Hanoi

Tower of Hanoi, is a mathematical puzzle which consists of three towers (pegs) and more than one rings is as depicted −

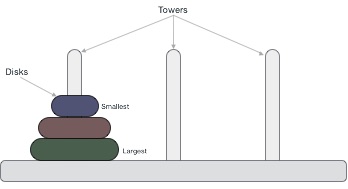
These rings are of different sizes and stacked upon in an ascending order, i.e. the smaller one sits over the larger one. There are other variations of the puzzle where the number of disks increase, but the tower count remains the same.

Rules

The mission is to move all the disks to some another tower without violating the sequence of arrangement. A few rules to be followed for Tower of Hanoi are −

Only one disk can be moved among the towers at any given time.
Only the "top" disk can be removed.
No large disk can sit over a small disk.

Following is an animated representation of solving a Tower of Hanoi puzzle with three disks.

Tower of Hanoi puzzle with n disks can be solved in minimum 2ⁿ−1 steps. This presentation shows that a puzzle with 3 disks has taken 2³ - 1 = 7 steps.

Algorithm

To write an algorithm for Tower of Hanoi, first we need to learn how to solve this problem with lesser amount of disks, say → 1 or 2. We mark three towers with name, source, destination and aux (only to help moving the disks). If we have only one disk, then it can easily be moved from source to destination peg.

If we have 2 disks −

First, we move the smaller (top) disk to aux peg.
Then, we move the larger (bottom) disk to destination peg.
And finally, we move the smaller disk from aux to destination peg.

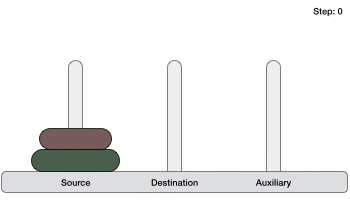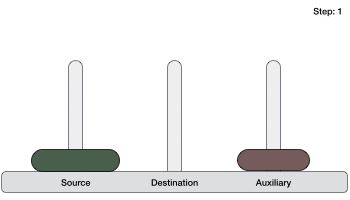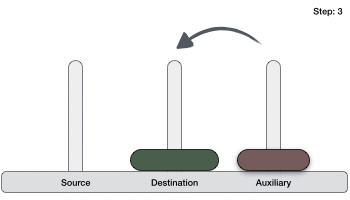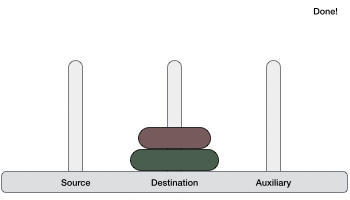
So now, we are in a position to design an algorithm for Tower of Hanoi with more than two disks. We divide the stack of disks in two parts. The largest disk (n^th disk) is in one part and all other (n-1) disks are in the second part.

Our ultimate aim is to move disk n from source to destination and then put all other (n1) disks onto it. We can imagine to apply the same in a recursive way for all given set of disks.

The steps to follow are −

Step 1 − Move n-1 disks from source to aux
Step 2 − Move n^th disk from source to dest
Step 3 − Move n-1 disks from aux to dest

A recursive algorithm for Tower of Hanoi can be driven as follows −

START
Procedure Hanoi(disk, source, dest, aux)

   IF disk == 1, THEN
      move disk from source to dest             
   ELSE
      Hanoi(disk - 1, source, aux, dest)     // Step 1
      move disk from source to dest          // Step 2
      Hanoi(disk - 1, aux, dest, source)     // Step 3
   END IF
   
END Procedure
STOP

To check the implementation in C programming, click here.

Data Structure & Algorithms Fibonacci Series

Fibonacci series generates the subsequent number by adding two previous numbers. Fibonacci series starts from two numbers − F₀ & F₁. The initial values of F₀ & F₁ can be taken 0, 1 or 1, 1 respectively.

Fibonacci series satisfies the following conditions −

F_n = F_n-1 + F_n-2

Hence, a Fibonacci series can look like this −

F₈ = 0 1 1 2 3 5 8 13

or, this −

F₈ = 1 1 2 3 5 8 13 21

For illustration purpose, Fibonacci of F₈ is displayed as −

Fibonacci Iterative Algorithm

First we try to draft the iterative algorithm for Fibonacci series.

Procedure Fibonacci(n)
   declare f₀, f₁, fib, loop 
   
   set f₀ to 0
   set f₁ to 1
   
   <b>display f₀, f₁</b>
   
   for loop ← 1 to n
   
      fib ← f₀ + f₁   
      f₀ ← f₁
      f₁ ← fib

      <b>display fib</b>
   end for
	
end procedure

To know about the implementation of the above algorithm in C programming language, click here.

Fibonacci Recursive Algorithm

Let us learn how to create a recursive algorithm Fibonacci series. The base criteria of recursion.

START
Procedure Fibonacci(n)
   declare f₀, f₁, fib, loop 
   
   set f₀ to 0
   set f₁ to 1
   
   display f₀, f₁
   
   for loop ← 1 to n
   
      fib ← f₀ + f₁   
      f₀ ← f₁
      f₁ ← fib

      display fib
   end for

END

To see the implementation of above algorithm in c programming language, click here.

Previous Page Print Page Next Page