Data Structure and Algorithms - Hash Table

---

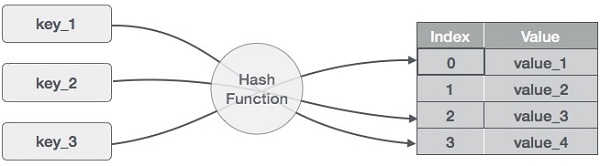
Hash Table is a data structure which stores data in an associative manner. In a hash table, data is stored in an array format, where each data value has its own unique index value. Access of data becomes very fast if we know the index of the desired data.

Thus, it becomes a data structure in which insertion and search operations are very fast irrespective of the size of the data. Hash Table uses an array as a storage medium and uses hash technique to generate an index where an element is to be inserted or is to be located from.

Hashing

Hashing is a technique to convert a range of key values into a range of indexes of an array. We're going to use modulo operator to get a range of key values. Consider an example of hash table of size 20, and the following items are to be stored. Item are in the (key,value) format.

• (1,20)
• (2,70)
• (42,80)
• (4,25)
• (12,44)
• (14,32)
• (17,11)
• (13,78)
• (37,98)

Sr.No.	Key	Hash	Array Index
1	1	1 % 20 = 1	1
2	2	2 % 20 = 2	2
3	42	42 % 20 = 2	2
4	4	4 % 20 = 4	4
5	12	12 % 20 = 12	12
6	14	14 % 20 = 14	14
7	17	17 % 20 = 17	17
8	13	13 % 20 = 13	13
9	37	37 % 20 = 17	17

Linear Probing

As we can see, it may happen that the hashing technique is used to create an already used index of the array. In such a case, we can search the next empty location in the array by looking into the next cell until we find an empty cell. This technique is called linear probing.

Sr.No.	Key	Hash	Array Index	After Linear Probing, Array Index
1	1	1 % 20 = 1	1	1
2	2	2 % 20 = 2	2	2
3	42	42 % 20 = 2	2	3
4	4	4 % 20 = 4	4	4
5	12	12 % 20 = 12	12	12
6	14	14 % 20 = 14	14	14
7	17	17 % 20 = 17	17	17
8	13	13 % 20 = 13	13	13
9	37	37 % 20 = 17	17	18

Basic Operations

Following are the basic primary operations of a hash table.

• Search − Searches an element in a hash table.

• Insert − inserts an element in a hash table.

• delete − Deletes an element from a hash table.

DataItem

Define a data item having some data and key, based on which the search is to be conducted in a hash table.

struct DataItem {
   int data;
   int key;
};

Hash Method

Define a hashing method to compute the hash code of the key of the data item.

int hashCode(int key){
   return key % SIZE;
}

Search Operation

Whenever an element is to be searched, compute the hash code of the key passed and locate the element using that hash code as index in the array. Use linear probing to get the element ahead if the element is not found at the computed hash code.

Example

struct DataItem *search(int key) {
   //get the hash
   int hashIndex = hashCode(key);
	
   //move in array until an empty
   while(hashArray[hashIndex] != NULL) {
	
      if(hashArray[hashIndex]->key == key)
         return hashArray[hashIndex];
			
      //go to next cell
      ++hashIndex;
		
      //wrap around the table
      hashIndex %= SIZE;
   }

   return NULL;        
}

Insert Operation

Whenever an element is to be inserted, compute the hash code of the key passed and locate the index using that hash code as an index in the array. Use linear probing for empty location, if an element is found at the computed hash code.

Example

void insert(int key,int data) {
   struct DataItem *item = (struct DataItem*) malloc(sizeof(struct DataItem));
   item->data = data;  
   item->key = key;     

   //get the hash 
   int hashIndex = hashCode(key);

   //move in array until an empty or deleted cell
   while(hashArray[hashIndex] != NULL && hashArray[hashIndex]->key != -1) {
      //go to next cell
      ++hashIndex;
		
      //wrap around the table
      hashIndex %= SIZE;
   }
	
   hashArray[hashIndex] = item;        
}

Delete Operation

Whenever an element is to be deleted, compute the hash code of the key passed and locate the index using that hash code as an index in the array. Use linear probing to get the element ahead if an element is not found at the computed hash code. When found, store a dummy item there to keep the performance of the hash table intact.

Example

struct DataItem* delete(struct DataItem* item) {
   int key = item->key;

   //get the hash 
   int hashIndex = hashCode(key);

   //move in array until an empty 
   while(hashArray[hashIndex] !=NULL) {
	
      if(hashArray[hashIndex]->key == key) {
         struct DataItem* temp = hashArray[hashIndex]; 
			
         //assign a dummy item at deleted position
         hashArray[hashIndex] = dummyItem; 
         return temp;
      } 
		
      //go to next cell
      ++hashIndex;
		
      //wrap around the table
      hashIndex %= SIZE;
   }  
	
   return NULL;        
}

To know about hash implementation in C programming language, please click here.