- PyTorch Tutorial
- PyTorch - Home
- PyTorch - Introduction
- PyTorch - Installation
- Mathematical Building Blocks of Neural Networks
- PyTorch - Neural Network Basics
- Universal Workflow of Machine Learning
- Machine Learning vs. Deep Learning
- Implementing First Neural Network
- Neural Networks to Functional Blocks
- PyTorch - Terminologies
- PyTorch - Loading Data
- PyTorch - Linear Regression
- PyTorch - Convolutional Neural Network
- PyTorch - Recurrent Neural Network
- PyTorch - Datasets
- PyTorch - Introduction to Convents
- Training a Convent from Scratch
- PyTorch - Feature Extraction in Convents
- PyTorch - Visualization of Convents
- Sequence Processing with Convents
- PyTorch - Word Embedding
- PyTorch - Recursive Neural Networks
- PyTorch Useful Resources
- PyTorch - Quick Guide
- PyTorch - Useful Resources
- PyTorch - Discussion
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
PyTorch - Linear Regression
In this chapter, we will be focusing on basic example of linear regression implementation using TensorFlow. Logistic regression or linear regression is a supervised machine learning approach for the classification of order discrete categories. Our goal in this chapter is to build a model by which a user can predict the relationship between predictor variables and one or more independent variables.
The relationship between these two variables is considered linear i.e., if y is the dependent variable and x is considered as the independent variable, then the linear regression relationship of two variables will look like the equation which is mentioned as below −
Y = Ax+b
Next, we shall design an algorithm for linear regression which allows us to understand two important concepts given below −
- Cost Function
- Gradient Descent Algorithms
The schematic representation of linear regression is mentioned below
Interpreting the result
$$Y=ax+b$$
The value of a is the slope.
The value of b is the y − intercept.
r is the correlation coefficient.
r2 is the correlation coefficient.
The graphical view of the equation of linear regression is mentioned below −
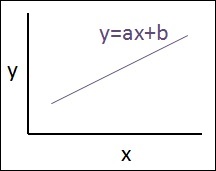
Following steps are used for implementing linear regression using PyTorch −
Step 1
Import the necessary packages for creating a linear regression in PyTorch using the below code −
import numpy as np import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation import seaborn as sns import pandas as pd %matplotlib inline sns.set_style(style = 'whitegrid') plt.rcParams["patch.force_edgecolor"] = True
Step 2
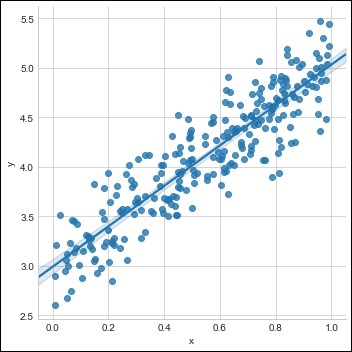
Create a single training set with the available data set as shown below −
m = 2 # slope c = 3 # interceptm = 2 # slope c = 3 # intercept x = np.random.rand(256) noise = np.random.randn(256) / 4 y = x * m + c + noise df = pd.DataFrame() df['x'] = x df['y'] = y sns.lmplot(x ='x', y ='y', data = df)
Step 3
Implement linear regression with PyTorch libraries as mentioned below −
import torch
import torch.nn as nn
from torch.autograd import Variable
x_train = x.reshape(-1, 1).astype('float32')
y_train = y.reshape(-1, 1).astype('float32')
class LinearRegressionModel(nn.Module):
def __init__(self, input_dim, output_dim):
super(LinearRegressionModel, self).__init__()
self.linear = nn.Linear(input_dim, output_dim)
def forward(self, x):
out = self.linear(x)
return out
input_dim = x_train.shape[1]
output_dim = y_train.shape[1]
input_dim, output_dim(1, 1)
model = LinearRegressionModel(input_dim, output_dim)
criterion = nn.MSELoss()
[w, b] = model.parameters()
def get_param_values():
return w.data[0][0], b.data[0]
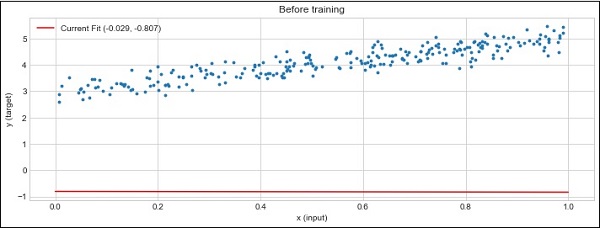
def plot_current_fit(title = ""):
plt.figure(figsize = (12,4))
plt.title(title)
plt.scatter(x, y, s = 8)
w1 = w.data[0][0]
b1 = b.data[0]
x1 = np.array([0., 1.])
y1 = x1 * w1 + b1
plt.plot(x1, y1, 'r', label = 'Current Fit ({:.3f}, {:.3f})'.format(w1, b1))
plt.xlabel('x (input)')
plt.ylabel('y (target)')
plt.legend()
plt.show()
plot_current_fit('Before training')
The plot generated is as follows −