
- PyTorch Tutorial
- PyTorch - Home
- PyTorch - Introduction
- PyTorch - Installation
- Mathematical Building Blocks of Neural Networks
- PyTorch - Neural Network Basics
- Universal Workflow of Machine Learning
- Machine Learning vs. Deep Learning
- Implementing First Neural Network
- Neural Networks to Functional Blocks
- PyTorch - Terminologies
- PyTorch - Loading Data
- PyTorch - Linear Regression
- PyTorch - Convolutional Neural Network
- PyTorch - Recurrent Neural Network
- PyTorch - Datasets
- PyTorch - Introduction to Convents
- Training a Convent from Scratch
- PyTorch - Feature Extraction in Convents
- PyTorch - Visualization of Convents
- Sequence Processing with Convents
- PyTorch - Word Embedding
- PyTorch - Recursive Neural Networks
- PyTorch Useful Resources
- PyTorch - Quick Guide
- PyTorch - Useful Resources
- PyTorch - Discussion
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
PyTorch - Neural Network Basics
The main principle of neural network includes a collection of basic elements, i.e., artificial neuron or perceptron. It includes several basic inputs such as x1, x2….. xn which produces a binary output if the sum is greater than the activation potential.
The schematic representation of sample neuron is mentioned below −
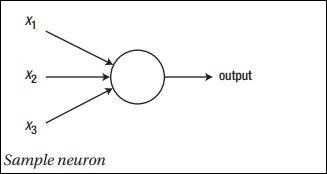
The output generated can be considered as the weighted sum with activation potential or bias.
$$Output=\sum_jw_jx_j+Bias$$
The typical neural network architecture is described below −
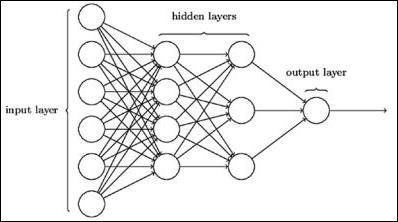
The layers between input and output are referred to as hidden layers, and the density and type of connections between layers is the configuration. For example, a fully connected configuration has all the neurons of layer L connected to those of L+1. For a more pronounced localization, we can connect only a local neighbourhood, say nine neurons, to the next layer. Figure 1-9 illustrates two hidden layers with dense connections.
The various types of neural networks are as follows −
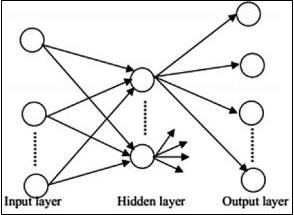
Feedforward Neural Networks
Feedforward neural networks include basic units of neural network family. The movement of data in this type of neural network is from the input layer to output layer, via present hidden layers. The output of one layer serves as the input layer with restrictions on any kind of loops in the network architecture.
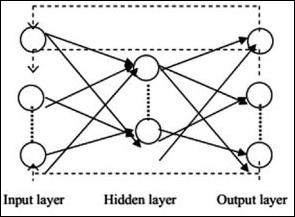
Recurrent Neural Networks
Recurrent Neural Networks are when the data pattern changes consequently over a period. In RNN, same layer is applied to accept the input parameters and display output parameters in specified neural network.
Neural networks can be constructed using the torch.nn package.
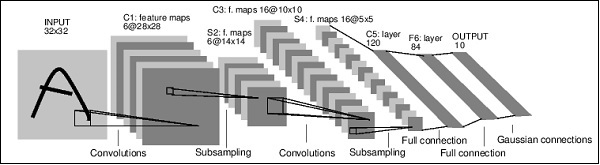
It is a simple feed-forward network. It takes the input, feeds it through several layers one after the other, and then finally gives the output.
With the help of PyTorch, we can use the following steps for typical training procedure for a neural network −
- Define the neural network that has some learnable parameters (or weights).
- Iterate over a dataset of inputs.
- Process input through the network.
- Compute the loss (how far is the output from being correct).
- Propagate gradients back into the network’s parameters.
- Update the weights of the network, typically using a simple update as given below
rule: weight = weight -learning_rate * gradient