Data Structure and Algorithms - Red Black Trees

---

Red-Black Trees are another type of the Balanced Binary Search Trees with two coloured nodes: Red and Black. It is a self-balancing binary search tree that makes use of these colours to maintain the balance factor during the insertion and deletion operations. Hence, during the Red-Black Tree operations, the memory uses 1 bit of storage to accommodate the colour information of each node

In Red-Black trees, also known as RB trees, there are different conditions to follow while assigning the colours to the nodes.

• The root node is always black in colour.

• No two adjacent nodes must be red in colour.

• Every path in the tree (from the root node to the leaf node) must have the same amount of black coloured nodes.

Even though AVL trees are more balanced than RB trees, with the balancing algorithm in AVL trees being stricter than that of RB trees, multiple and faster insertion and deletion operations are made more efficient through RB trees.

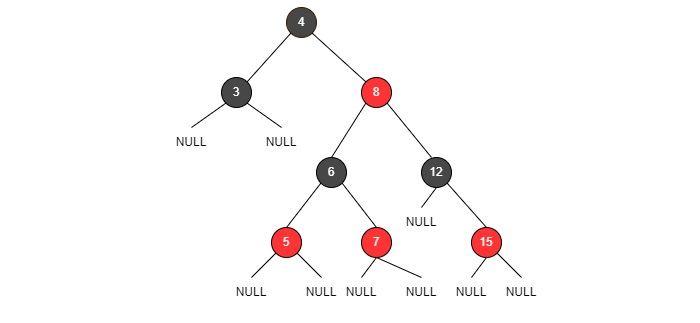
Fig: RB trees

Basic Operations of Red-Black Trees

The operations on Red-Black Trees include all the basic operations usually performed on a Binary Search Tree. Some of the basic operations of an RB Tree include −

• Insertion

• Deletion

• Search

Insertion operation of a Red-Black tree follows the same insertion algorithm of a binary search tree. The elements are inserted following the binary search property and as an addition, the nodes are color coded as red and black to balance the tree according to the red-black tree properties.

Follow the procedure given below to insert an element into a red-black tree by maintaining both binary search tree and red black tree properties.

Case 1 − Check whether the tree is empty; make the current node as the root and color the node black if it is empty.

Case 2 − But if the tree is not empty, we create a new node and color it red. Here we face two different cases −

• If the parent of the new node is a black colored node, we exit the operation and tree is left as it is.

• If the parent of this new node is red and the color of the parent’s sibling is either black or if it does not exist, we apply a suitable rotation and recolor accordingly.

• If the parent of this new node is red and color of the parent’s sibling is red, recolor the parent, the sibling and grandparent nodes to black. The grandparent is recolored only if it is not the root node; if it is the root node recolor only the parent and the sibling.

Insertion Example

Let us construct an RB Tree for the first 7 integer numbers to understand the insertion operation in detail −

The tree is checked to be empty so the first node added is a root and is colored black.

Now, the tree is not empty so we create a new node and add the next integer with color red,

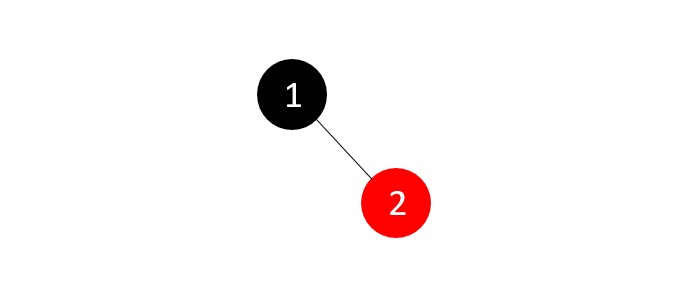
The nodes do not violate the binary search tree and RB tree properties, hence we move ahead to add another node.

The tree is not empty; we create a new red node with the next integer to it. But the parent of the new node is not a black colored node,

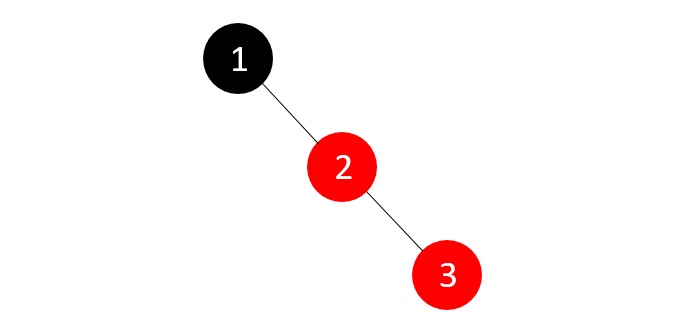
The tree right now violates both the binary search tree and RB tree properties; since parent’s sibling is NULL, we apply a suitable rotation and recolor the nodes.

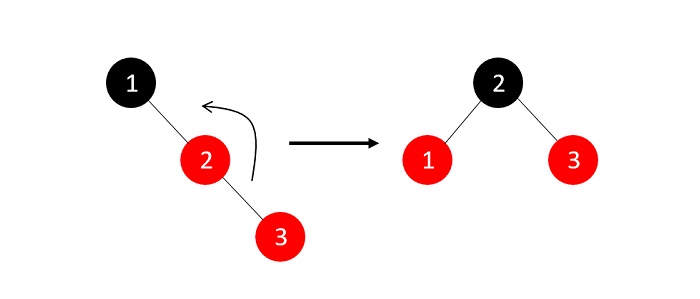
Now that the RB Tree property is restored, we add another node to the tree −

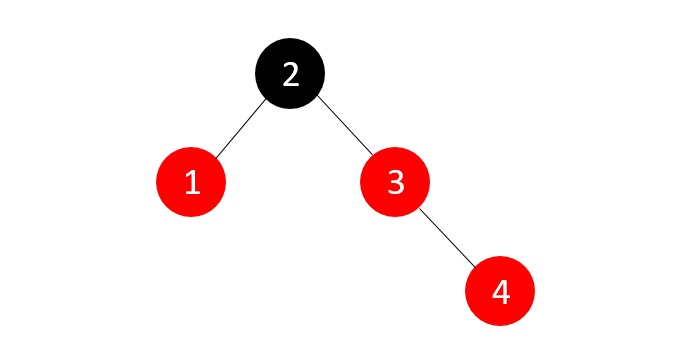
The tree once again violates the RB Tree balance property, so we check for the parent’s sibling node color, red in this case, so we just recolor the parent and the sibling.

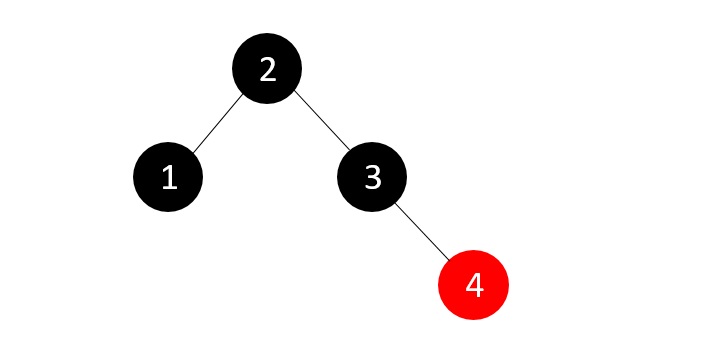
We next insert the element 5, which makes the tree violate the RB Tree balance property once again.

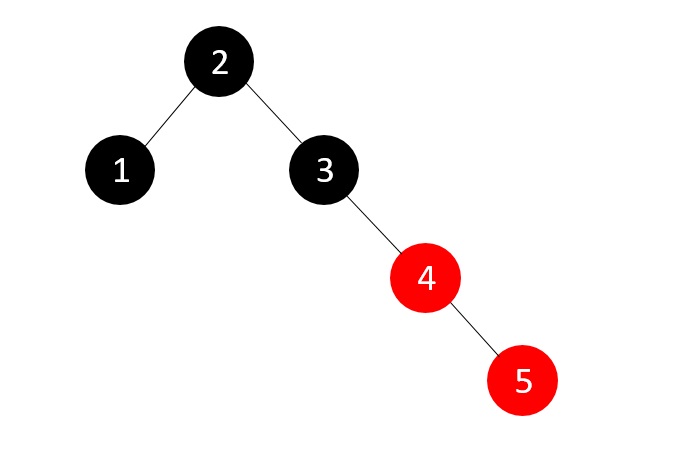
And since the sibling is NULL, we apply suitable rotation and recolor.

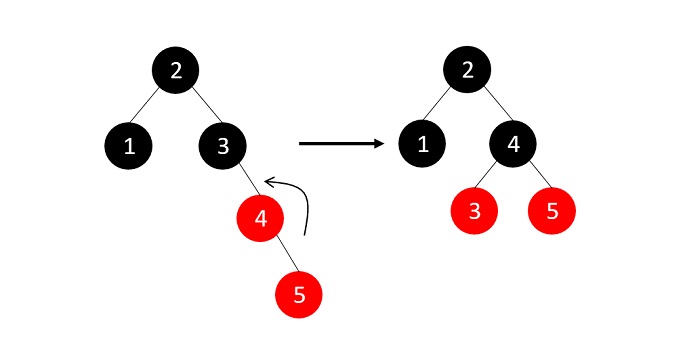
Now, we insert element 6, but the RB Tree property is violated and one of the insertion cases need to be applied −

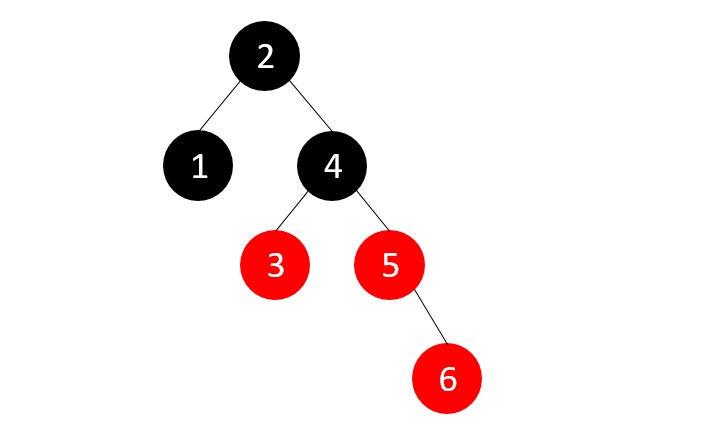
The parent’s sibling is red, so we recolor the parent, parent’s sibling and the grandparent nodes since the grandparent is not the root node.

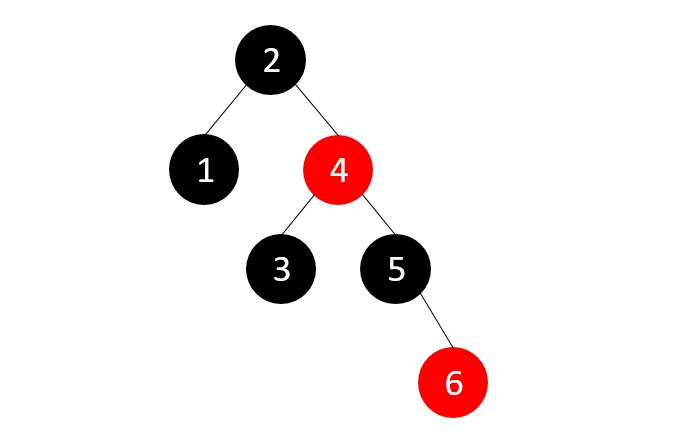
Now, we add the last element, 7, but the parent node of this new node is red.

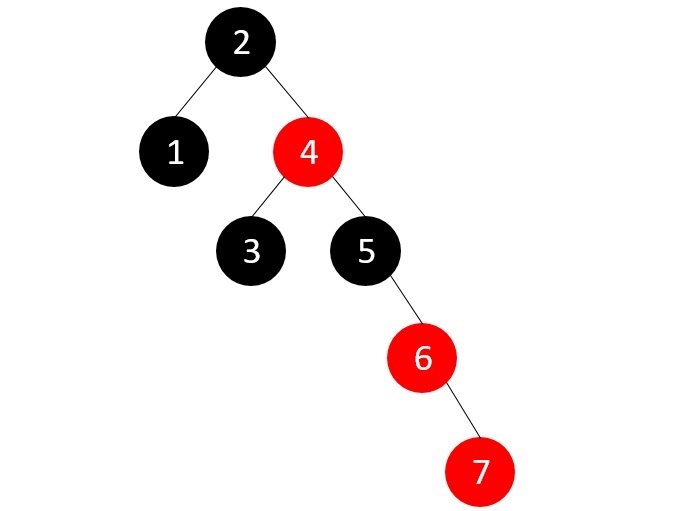
Since the parent’s sibling is NULL, we apply suitable rotations (RR rotation)

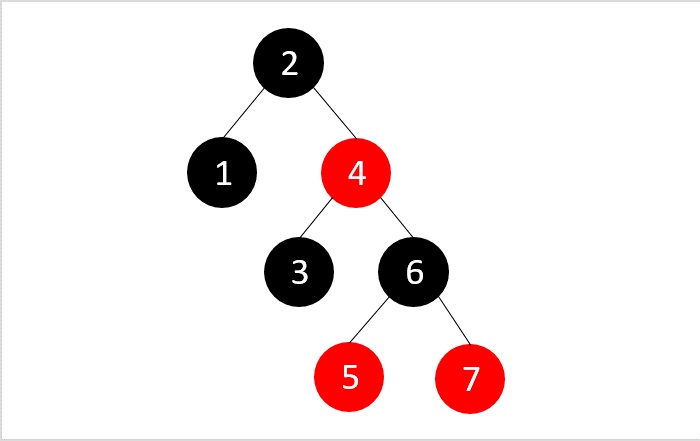
The final RB Tree is achieved.

Deletion

The deletion operation on red black tree must be performed in such a way that it must restore all the properties of a binary search tree and a red black tree. Follow the steps below to perform the deletion operation on the red black tree −

Firstly, we perform deletion based on the binary search tree properties.

Case 1 − If either the node to be deleted or the node’s parent is red, just delete it.

Case 2 − If the node is a double black, just remove the double black (double black occurs when the node to be deleted is a black colored leaf node, as it adds up the NULL nodes which are considered black colored nodes too)

Case 3 − If the double black’s sibling node is also a black node and its child nodes are also black in color, follow the steps below −

• Remove double black

• Recolor its parent to black (if the parent is a red node, it becomes black; if the parent is already a black node, it becomes double black)

• Recolor the parent’s sibling with red

• If double black node still exists, we apply other cases.

Case 4 − If the double black node’s sibling is red, we perform the following steps −

• Swap the colors of the parent node and the parent’s sibling node.

• Rotate parent node in the double black’s direction

• Reapply other cases that are suitable.

Case 5 − If the double black’s sibling is a black node but the sibling’s child node that is closest to the double black is red, follows the steps below −

• Swap the colors of double black’s sibling and the sibling’s child in question

• Rotate the sibling node is the opposite direction of double black (i.e. if the double black is a right child apply left rotations and vice versa)

• Apply case 6.

Case 6 − If the double black’s sibling is a black node but the sibling’s child node that is farther to the double black is red, follows the steps below −

• Swap the colors of double black’s parent and sibling nodes

• Rotate the parent in double black’s direction (i.e. if the double black is a right child apply right rotations and vice versa)

• Remove double black

• Change the color of red child node to black.

Deletion Example

Considering the same constructed Red-Black Tree above, let us delete few elements from the tree.

Delete elements 4, 5, 3 from the tree.

To delete the element 4, let us perform the binary search deletion first.

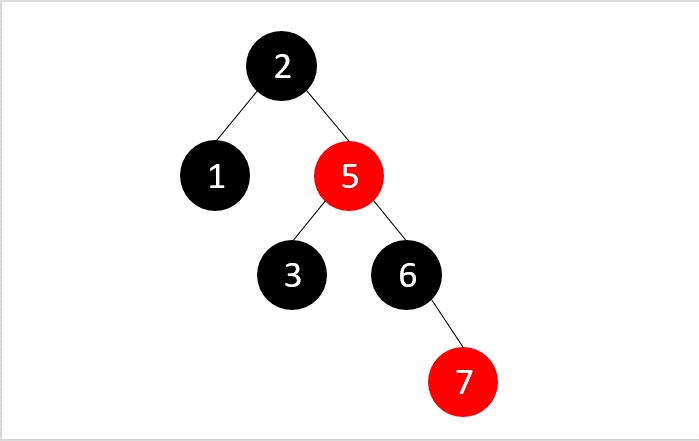
After performing the binary search deletion, the RB Tree property is not disturbed, therefore the tree is left as it is.

Then, we delete the element 5 using the binary search deletion

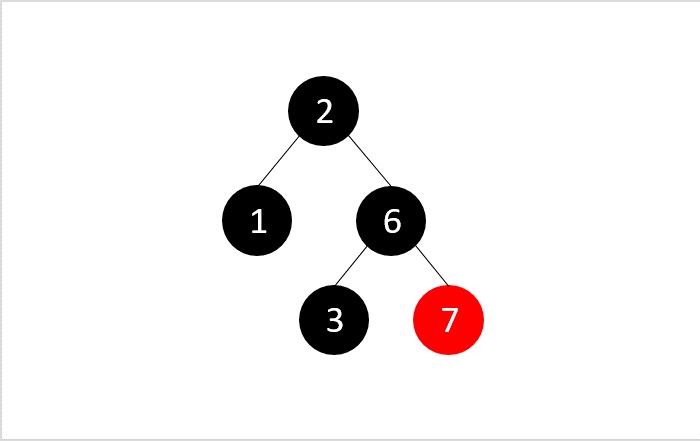
But the RB property is violated after performing the binary search deletion, i.e., all the paths in the tree do not hold same number of black nodes; so we swap the colors to balance the tree.

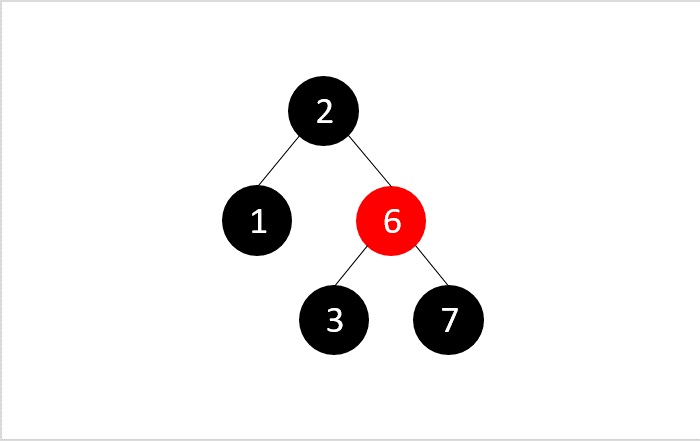
Then, we delete the node 3 from the tree obtained −

Applying binary search deletion, we delete node 3 normally as it is a leaf node. And we get a double node as 3 is a black colored node.

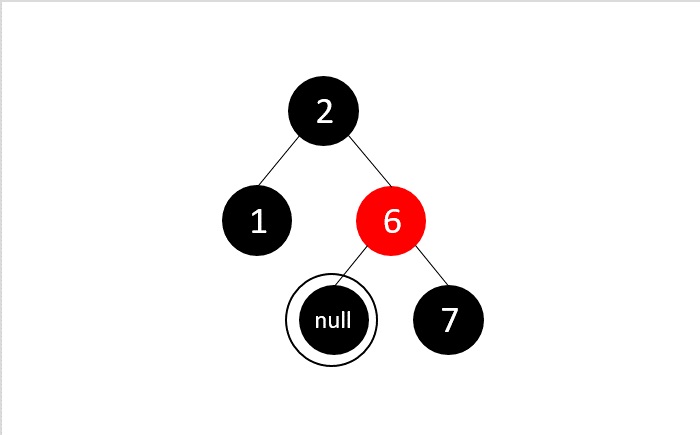
We apply case 3 deletion as double black’s sibling node is black and its child nodes are also black. Here, we remove the double black, recolor the double black’s parent and sibling.

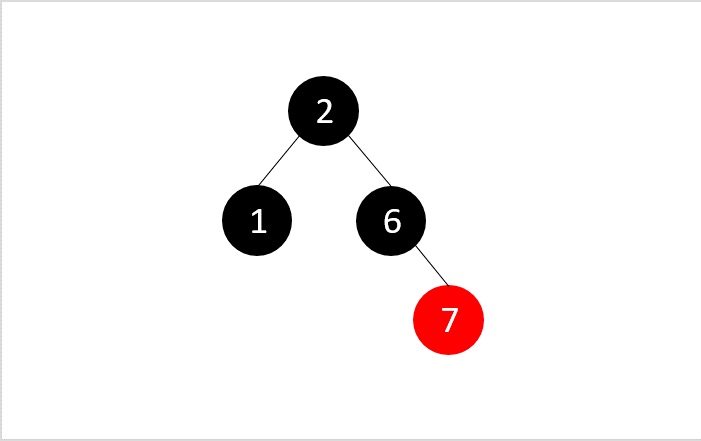
All the desired nodes are deleted and the RB Tree property is maintained.

Search

The search operation in red-black tree follows the same algorithm as that of a binary search tree. The tree is traversed and each node is compared with the key element to be searched; if found it returns a successful search. Otherwise, it returns an unsuccessful search.