Teach with us

Data Structure & Algorithms - Tree Traversal

Previous Page
Next Page  

Traversal is a process to visit all the nodes of a tree and may print their values too. Because, all nodes are connected via edges (links) we always start from the root (head) node. That is, we cannot randomly access a node in a tree. There are three ways which we use to traverse a tree −

  • In-order Traversal

  • Pre-order Traversal

  • Post-order Traversal

Generally, we traverse a tree to search or locate a given item or key in the tree or to print all the values it contains.

In-order Traversal

In this traversal method, the left subtree is visited first, then the root and later the right sub-tree. We should always remember that every node may represent a subtree itself.

If a binary tree is traversed in-order, the output will produce sorted key values in an ascending order.

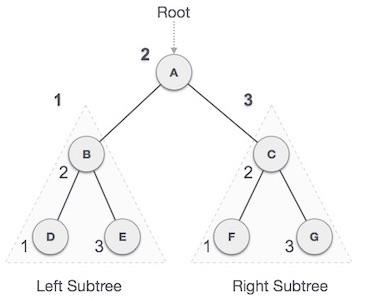
In-order Traversal

We start from A, and following in-order traversal, we move to its left subtree B.B is also traversed in-order. The process goes on until all the nodes are visited. The output of in-order traversal of this tree will be −

D → B → E → A → F → C → G

Algorithm

Until all nodes are traversed −

Step 1 − Recursively traverse left subtree.

Step 2 − Visit root node.

Step 3 − Recursively traverse right subtree.

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python 
#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void inorder_traversal(struct node* root){
   if(root != NULL) {
      inorder_traversal(root->leftChild);
      printf("%d ",root->data);
      inorder_traversal(root->rightChild);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("\nInorder traversal: ");
   inorder_traversal(root);
   return 0;
}

Output

Inorder traversal: 10 14 19 27 31 35 42

#include <iostream>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void inorder_traversal(struct node* root){
   if(root != NULL) {
      inorder_traversal(root->leftChild);
      printf("%d ",root->data);
      inorder_traversal(root->rightChild);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("\nInorder traversal: ");
   inorder_traversal(root);
   return 0;
}

Output

Inorder traversal: 10 14 19 27 31 35 42 

class Node {
   int data;
   Node leftChild;
   Node rightChild;
   public Node(int key) {
      data = key;
      leftChild = rightChild = null;
   }
}
public class TreeDataStructure {
   Node root = null;
   void inorder_traversal(Node node) {
      if(node != null) {
         inorder_traversal(node.leftChild);
         System.out.print(node.data + " ");
         inorder_traversal(node.rightChild);
      }
   }
   public static void main(String args[]) {
      TreeDataStructure tree = new TreeDataStructure();
      tree.root = new Node(27);
      tree.root.leftChild = new Node(12);
      tree.root.rightChild = new Node(3);
      tree.root.leftChild.leftChild = new Node(44);
      tree.root.leftChild.rightChild = new Node(17);
      tree.root.rightChild.leftChild = new Node(56);
      System.out.println("\nInorder traversal: ");
      tree.inorder_traversal(tree.root);
   }
}

Output

Inorder traversal: 
44 12 17 27 56 3 

class Node:
   def __init__(self, key):
      self.leftChild = None
      self.rightChild = None
      self.data = key

# Create a function to perform inorder tree traversal
def InorderTraversal(root):
   if root:
      InorderTraversal(root.leftChild)
      print(root.data)
      InorderTraversal(root.rightChild)

# Main class
if __name__ == "__main__":
   root = Node(3)
   root.leftChild = Node(26)
   root.rightChild = Node(42)
   root.leftChild.leftChild = Node(54)
   root.leftChild.rightChild = Node(65)
   root.rightChild.leftChild = Node(12)

   # Function call
   print("\nInorder traversal of binary tree is")
   InorderTraversal(root)

Output

Inorder traversal of binary tree is
54
26
65
3
12
42

Pre-order Traversal

In this traversal method, the root node is visited first, then the left subtree and finally the right subtree.

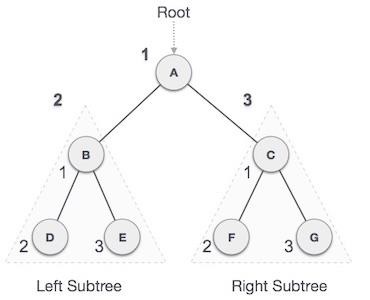
Pre-order Traversal

We start from A, and following pre-order traversal, we first visit A itself and then move to its left subtree B. B is also traversed pre-order. The process goes on until all the nodes are visited. The output of pre-order traversal of this tree will be −

A → B → D → E → C → F → G

Algorithm

Until all nodes are traversed −

Step 1 − Visit root node.

Step 2 − Recursively traverse left subtree.

Step 3 − Recursively traverse right subtree.

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python 
#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void pre_order_traversal(struct node* root){
   if(root != NULL) {
      printf("%d ",root->data);
      pre_order_traversal(root->leftChild);
      pre_order_traversal(root->rightChild);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("\nPreorder traversal: ");
   pre_order_traversal(root);
   return 0;
}

Output

Preorder traversal: 27 14 10 19 35 31 42 

#include <iostream>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void pre_order_traversal(struct node* root){
   if(root != NULL) {
      printf("%d ",root->data);
      pre_order_traversal(root->leftChild);
      pre_order_traversal(root->rightChild);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("\nPreorder traversal: ");
   pre_order_traversal(root);
   return 0;
}

Output

Preorder traversal: 27 14 10 19 35 31 42 

class Node {
   int data;
   Node leftChild;
   Node rightChild;
   public Node(int key) {
      data = key;
      leftChild = rightChild = null;
   }
}
public class TreeDataStructure {
   Node root = null;
   void pre_order_traversal(Node node) {
      if(node != null) {
         System.out.print(node.data + " ");
         pre_order_traversal(node.leftChild);
         pre_order_traversal(node.rightChild);
      }
   }
   public static void main(String args[]) {
      TreeDataStructure tree = new TreeDataStructure();
      tree.root = new Node(27);
      tree.root.leftChild = new Node(12);
      tree.root.rightChild = new Node(3);
      tree.root.leftChild.leftChild = new Node(44);
      tree.root.leftChild.rightChild = new Node(17);
      tree.root.rightChild.leftChild = new Node(56);
      System.out.println("\nPreorder traversal: ");
      tree.pre_order_traversal(tree.root);
   }
}

Output

Preorder traversal: 
27 12 44 17 3 56 

class Node:
   def __init__(self, key):
      self.leftChild = None
      self.rightChild = None
      self.data = key

# Create a function to perform postorder tree traversal
def PreorderTraversal(root):
   if root:
      print(root.data)
      PreorderTraversal(root.leftChild)
      PreorderTraversal(root.rightChild)

# Main class
if __name__ == "__main__":
   root = Node(3)
   root.leftChild = Node(26)
   root.rightChild = Node(42)
   root.leftChild.leftChild = Node(54)
   root.leftChild.rightChild = Node(65)
   root.rightChild.leftChild = Node(12)
   print("\nPreorder traversal of binary tree is")
   PreorderTraversal(root)

Output

Preorder traversal of binary tree is
3
26
54
65
42
12

Post-order Traversal

In this traversal method, the root node is visited last, hence the name. First we traverse the left subtree, then the right subtree and finally the root node.

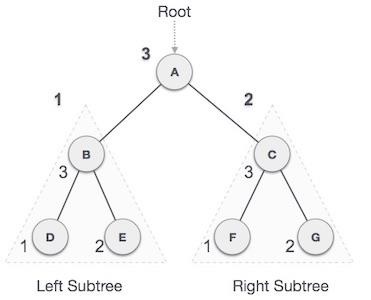
Post-order Traversal

We start from A, and following pre-order traversal, we first visit the left subtree B. B is also traversed post-order. The process goes on until all the nodes are visited. The output of post-order traversal of this tree will be −

D → E → B → F → G → C → A

Algorithm

Until all nodes are traversed −

Step 1 − Recursively traverse left subtree.

Step 2 − Recursively traverse right subtree.

Step 3 − Visit root node.

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python 
#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void post_order_traversal(struct node* root){
   if(root != NULL) {
      post_order_traversal(root->leftChild);
      post_order_traversal(root->rightChild);
      printf("%d ", root->data);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("\nPost order traversal: ");
   post_order_traversal(root);
   return 0;
}

Output

Post order traversal: 10 19 14 31 42 35 27 

#include <iostream>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void post_order_traversal(struct node* root){
   if(root != NULL) {
      post_order_traversal(root->leftChild);
      post_order_traversal(root->rightChild);
      printf("%d ", root->data);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("\nPost order traversal: ");
   post_order_traversal(root);
   return 0;
}

Output

Post order traversal: 10 19 14 31 42 35 27

class Node {
   int data;
   Node leftChild;
   Node rightChild;
   public Node(int key) {
      data = key;
      leftChild = rightChild = null;
   }
}
public class TreeDataStructure {
   Node root = null;
   void post_order_traversal(Node node) {
      if(node != null) {
         post_order_traversal(node.leftChild);
         post_order_traversal(node.rightChild);
         System.out.print(node.data + " ");
      }
   }
   public static void main(String args[]) {
      TreeDataStructure tree = new TreeDataStructure();
      tree.root = new Node(27);
      tree.root.leftChild = new Node(12);
      tree.root.rightChild = new Node(3);
      tree.root.leftChild.leftChild = new Node(44);
      tree.root.leftChild.rightChild = new Node(17);
      tree.root.rightChild.leftChild = new Node(56);
      System.out.println("\nPost order traversal: ");
      tree.post_order_traversal(tree.root);
   }
}

Output

Post order traversal: 
44 17 12 56 3 27 

class Node:
   def __init__(self, key):
      self.leftChild = None
      self.rightChild = None
      self.data = key

# Create a function to perform preorder tree traversal
def PostorderTraversal(root):
   if root:
      PostorderTraversal(root.leftChild)
      PostorderTraversal(root.rightChild)
      print(root.data)

# Main class
if __name__ == "__main__":
   root = Node(3)
   root.leftChild = Node(26)
   root.rightChild = Node(42)
   root.leftChild.leftChild = Node(54)
   root.leftChild.rightChild = Node(65)
   root.rightChild.leftChild = Node(12)
   print("\nPostorder traversal of binary tree is")
   PostorderTraversal(root)

Output

Postorder traversal of binary tree is
54
65
26
12
42
3

To check the C implementation of tree traversing, please click here

Implementation

Traversal is a process to visit all the nodes of a tree and may print their values too. Because, all nodes are connected via edges (links) we always start from the root (head) node. That is, we cannot randomly access a node in a tree. There are three ways which we use to traverse a tree −

  • In-order Traversal

  • Pre-order Traversal

  • Post-order Traversal

We shall now see the implementation of tree traversal in C programming language here using the following binary tree −

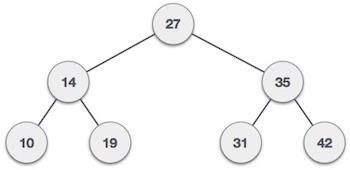
Tree Traversal

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python 
#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

//if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void pre_order_traversal(struct node* root){
   if(root != NULL) {
      printf("%d ",root->data);
      pre_order_traversal(root->leftChild);
      pre_order_traversal(root->rightChild);
   }
}
void inorder_traversal(struct node* root){
   if(root != NULL) {
      inorder_traversal(root->leftChild);
      printf("%d ",root->data);
      inorder_traversal(root->rightChild);
   }
}
void post_order_traversal(struct node* root){
   if(root != NULL) {
      post_order_traversal(root->leftChild);
      post_order_traversal(root->rightChild);
      printf("%d ", root->data);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("\nPreorder traversal: ");
   pre_order_traversal(root);
   printf("\nInorder traversal: ");
   inorder_traversal(root);
   printf("\nPost order traversal: ");
   post_order_traversal(root);
   return 0;
}

Output

Preorder traversal: 27 14 10 19 35 31 42 
Inorder traversal: 10 14 19 27 31 35 42 
Post order traversal: 10 19 14 31 42 35 27

#include <iostream>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void pre_order_traversal(struct node* root){
   if(root != NULL) {
      printf("%d ",root->data);
      pre_order_traversal(root->leftChild);
      pre_order_traversal(root->rightChild);
   }
}
void inorder_traversal(struct node* root){
   if(root != NULL) {
      inorder_traversal(root->leftChild);
      printf("%d ",root->data);
      inorder_traversal(root->rightChild);
   }
}
void post_order_traversal(struct node* root){
   if(root != NULL) {
      post_order_traversal(root->leftChild);
      post_order_traversal(root->rightChild);
      printf("%d ", root->data);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("\nPreorder traversal: ");
   pre_order_traversal(root);
   printf("\nInorder traversal: ");
   inorder_traversal(root);
   printf("\nPost order traversal: ");
   post_order_traversal(root);
   return 0;
}

Output

Preorder traversal: 27 14 10 19 35 31 42 
Inorder traversal: 10 14 19 27 31 35 42 
Post order traversal: 10 19 14 31 42 35 27 

class Node {
   int data;
   Node leftChild;
   Node rightChild;
   public Node(int key) {
      data = key;
      leftChild = rightChild = null;
   }
}
public class TreeDataStructure {
   Node root = null;
   void inorder_traversal(Node node) {
      if(node != null) {
         inorder_traversal(node.leftChild);
         System.out.print(node.data + " ");
         inorder_traversal(node.rightChild);
      }
   }
   void pre_order_traversal(Node node) {
      if(node != null) {
         System.out.print(node.data + " ");
         pre_order_traversal(node.leftChild);
         pre_order_traversal(node.rightChild);
      }
   }
   void post_order_traversal(Node node) {
      if(node != null) {
         post_order_traversal(node.leftChild);
         post_order_traversal(node.rightChild);
         System.out.print(node.data + " ");
      }
   }
   public static void main(String args[]) {
      TreeDataStructure tree = new TreeDataStructure();
      tree.root = new Node(27);
      tree.root.leftChild = new Node(12);
      tree.root.rightChild = new Node(3);
      tree.root.leftChild.leftChild = new Node(44);
      tree.root.leftChild.rightChild = new Node(17);
      tree.root.rightChild.leftChild = new Node(56);
      System.out.println("\nInorder traversal: ");
      tree.inorder_traversal(tree.root);
      System.out.println("\nPreorder traversal: ");
      tree.pre_order_traversal(tree.root);
      System.out.println("\nPost order traversal: ");
      tree.post_order_traversal(tree.root);
   }
}

Output

Inorder traversal: 
44 12 17 27 56 3 
Preorder traversal: 
27 12 44 17 3 56 
Post order traversal: 
44 17 12 56 3 27 

class Node:
   def __init__(self, key):
      self.leftChild = None
      self.rightChild = None
      self.data = key

# Create a function to perform inorder tree traversal
def InorderTraversal(root):
   if root:
      InorderTraversal(root.leftChild)
      print(root.data)
      InorderTraversal(root.rightChild)

# Create a function to perform preorder tree traversal
def PostorderTraversal(root):
   if root:
      PostorderTraversal(root.leftChild)
      PostorderTraversal(root.rightChild)
      print(root.data)

# Create a function to perform postorder tree traversal
def PreorderTraversal(root):
   if root:
      print(root.data)
      PreorderTraversal(root.leftChild)
      PreorderTraversal(root.rightChild)

# Main class
if __name__ == "__main__":
   root = Node(3)
   root.leftChild = Node(26)
   root.rightChild = Node(42)
   root.leftChild.leftChild = Node(54)
   root.leftChild.rightChild = Node(65)
   root.rightChild.leftChild = Node(12)

   # Function call
   print("\nInorder traversal of binary tree is")
   InorderTraversal(root)
   print("\nPreorder traversal of binary tree is")
   PreorderTraversal(root)
   print("\nPostorder traversal of binary tree is")
   PostorderTraversal(root)

Output

Inorder traversal of binary tree is
54
26
65
3
12
42

Preorder traversal of binary tree is
3
26
54
65
42
12

Postorder traversal of binary tree is
54
65
26
12
42
3
Previous Page Print Page Next Page  
Advertisements